在短期内，我们假定资本作为一种不变投入要素，通过分析具有可变技术系数的生产函数，介绍生产函数的有关概念。

1.短期生产函数的概念

厂商在一定技术条件下用劳动和资本生产一种产品，厂商的可变投入只有劳动，资本为不变投入，此时短期生产函数可写成：

式中，Q表示产量，L表示劳动，K表示资本。式（5-3）考查的就是只有一种可变投入的生产函数，借助它来讨论投入与产出的关系。

2.总产量、平均产量和边际产量

首先我们要说明总产量TP、平均产量AP和边际产量MP这三个概念。

在一定技术条件下，一种投入或生产要素的总产量（total product）就是从一定量该种生产要素中所获得的产量的总和。对于式（5-3）而言，资本的投入量不变，用TP表示劳动的总产量，则：

劳动的平均产量（average product）指平均每个单位劳动所生产的产量，等于劳动生产的总产量除以劳动的投入量。用AP表示劳动的平均产量，则：

每增加一单位劳动所引起的总产量变动，被称为劳动的边际产量（marginal product），用MP表示，则：

如果劳动数量可以无限分割，当总产量函数为连续函数且可以求导时，则边际产量可写为：

一条简单的短期生产函数可通过设定的生产函数的列表和生产函数曲线进行分析。在资本投入固定不变时，投入不同量的劳动所得到的总产量、平均产量和边际产量，如表5-2所示。

表5-2　只有劳动作为可变投入时的生产函数举例

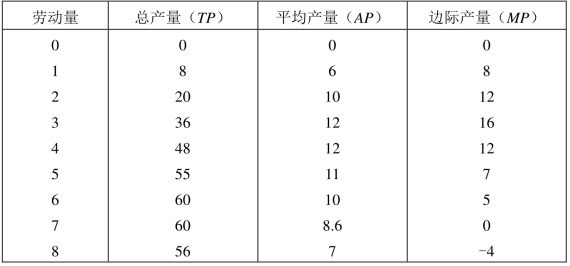
根据表中变量间的对应关系可以绘制出短期生产函数曲线，即总产量曲线、平均产量曲线和边际产量曲线，如图5-1所示。

案例5.2 在土地上施肥量越多越好吗

早在1771年英国农学家杨格就用在若干相同的地块上施以不同量肥料的实验，证明了肥料施用量与产量增加之间存在着这种边际产量递减的关系。这不是偶然的现象而是经验性规律。假如农民在一亩土地上撒一把化肥能增加产量1公斤，撒两把化肥增产3公斤，但一把一把化肥的增产效果会越来越差，过量的施肥量甚至会导致土壤板结、粮食减产。边际产量递减规律是从社会生产实践和科学实验中总结出来的，在现实生活的绝大多数生产过程中都是适用的。如果是边际产量递增，那么全世界有一亩土地就能养活全世界所有的人，那才是不可思议的了。

用两种（或两种以上）生产要素相结合生产一种产品时，如果其中一种要素是可以变动的，那么，在其他条件不变的情况下，随着这一可变要素连续地等量增加，其边际产量开始会出现递增的现象，但在达到一定数量后，会呈现递减现象。这就是经济学中著名的边际产量递减规律。边际产量递减规律提示我们，在一定的条件下，高投入未必带来高产出，因此要注意投入的合理限度，寻找最佳的投入数量。在现实生活中边际产量递减的例子很多，目前我国的就业压力很大，其实也是这个规律作用的结果，如果是边际产量递增我们就不会有失业问题了。

摘自blog.sina.com.cn

3.边际报酬递减规律

由表5-2和图5-1可以清楚地看到，对只有一种可变投入的生产函数来说，边际产量具有最终下降的特征，即具有边际报酬递减的特征。就是说，在其他要素投入量保持不变的情况下，如果连续追加相同数量的某种生产要素，其产量的增量在达到某一点后会下降，即可变生产要素的边际产量会递减，对一种可变生产要素的生产函数来说，边际产量表现出先上升而最终下降的规律。这就是边际报酬递减规律。从图5-1中可以看出，当劳动的投入量达到3单位后，劳动的边际产量开始下降。(www.daowen.com)

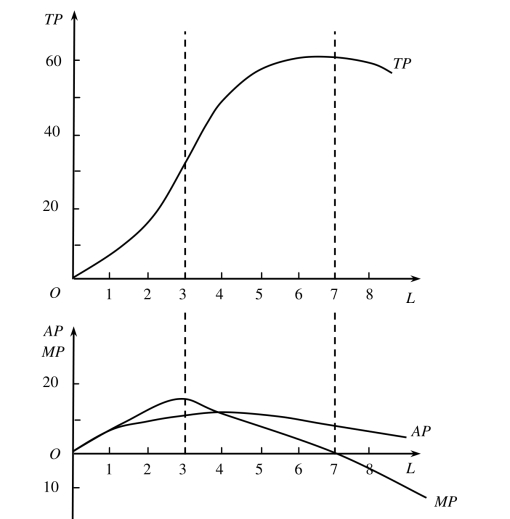
图5-1　劳动的总产量、平均产量和边际产量

边际报酬递减规律存在的原因是：随着可变要素投入量的增加，可变要素的投入量与固定要素的投入量之间的比例在发生变化。在可变要素的投入量增加的最初阶段，相对于固定要素的投入量来说，可变要素的投入量过少，因此，随着可变要素投入量的增加，其边际产量递增，当可变要素投入量与固定要素投入量的配合比例恰当时，边际产量达到最大。如果再继续增加可变要素的投入量，由于其他要素的数量是固定的，可变要素就相对过多，于是边际产量就必然递减。也就是说，在产品的生产过程中，不变要素投入和可变要素投入之间存在着一个最佳组合比例。由于不变要素投入量总是存在的，随着可变要素投入量逐渐增加，生产要素的组合逐渐接近最佳组合比例，可变要素的边际产量递增。生产要素的组合达到最佳组合比例时，可变要素的边际产量达到最大值。此后，随着可变要素投入量继续增加，生产要素的组合逐渐偏离最佳组合比例，可变要素的边际产量递减。

边际报酬递减规律决定了边际产量曲线呈先升后降的特征。

关于边际报酬递减规律应说明以下几点：第一，该规律只是一个经验的概括，而不是物理学或生物学规律的推演，但它对于现实中大多数生产函数都是适用的；第二，这一规律以技术不变为假定前提，它不能预示在技术变化时增加一单位生产要素所产生的影响；第三，它假定至少有一种生产要素或投入的数量保持不变，它不适用于所有的生产要素按相同比例增加时的情况；第四，当然，改变所使用的生产要素的比例必须是可能的，或者说，生产函数的技术系数必须是可变的。

案例5.3 中国人养活自己靠的是农业技术进步

边际产量递减规律早在18世纪就由经济学家提出，有人把这一规律应用到农业领域却描述出一幅人类前景悲惨的画面来：因为耕地等自然资源毕竟是有限的，要增产粮食最终只能依靠劳动力的增加，但边际产量递减规律表明，劳动力投入带来的边际粮食产量递减，于是人口不断增长的必然结果是，人类不能养活自己。无独有偶，1994年，一位叫莱斯特·布朗的人重复类似悲观的预言，发表了一本题为《谁来养活中国》的小册子，宣称人口众多的中国将面临粮食短缺，进而引发全球粮价猛涨的危机。杞人忧天的布朗是否知道袁隆平的名字，他利用科学技术发明了杂交水稻，使每亩单产达到了405公斤，小麦从50公斤提高到目前的700公斤。中国有出色的农业科学家，中国人养活自己靠的是农业技术进步。布朗先生实在是用错了边际产量递减规律。要记住边际产量递减规律是有条件的。

著名经济学家克拉克较早地发现了这一规律，他曾指出，“知识是唯一不遵守效益递减规律的工具”。如美国微软公司为开发第一套视窗软件投入了5000万美元，其额外生产上千万套只需复制即可，成本几乎可以不计，但仍能以与第一套同样的价格发行，这样，在新经济部门，就出现了不同于传统产业部门的“边际效益递增”的情况。

边际产量递减规律适用的条件是在技术水平不变的情况下（其他条件不变），随着这一可变要素连续地等量增加，其边际产量开始会出现递增的现象，但在达到一定数量后，会呈现递减现象。如果技术等其他条件发生了变化，由于信息等高科技产业以知识为基础，而知识具有可共享、可重复使用、可低成本复制、可发展等特点，对其使用和改进越多，其创造的价值越大，“边际效益递增”。这一观点是对新古典微观经济学的巨大挑战。

资料来源：梁小民主编.西方经济学

4.平均产量、边际产量与总产量的关系

上述可变要素的边际产量、平均产量和总产量之间的关系可通过几何测定的方法得到说明。图5-2所描述的是一条相对于一个可变要素比如劳动的总产量曲线。我们先来看劳动的边际产量是如何测定的。曲线上任何一点的斜率（即该点的切线的斜率）为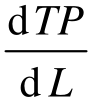，这就是劳动在该点的边际产量值。所以，我们可以通过计算总产量曲线上任一点的切线的斜率，来测定相对于该点的可变要素的边际产量。例如，TP曲线上A点的斜率最大，此时边际产量也达到最大值，即TP曲线上A点的斜率值；TP曲线上C点的斜率为零，边际产量此时也为零。

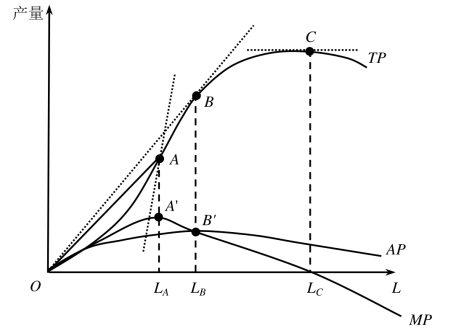
图5-2　边际产量和平均产量的测定

下面再来看劳动的平均产量是如何测定的。既然可变要素的平均产量等于总产量除以可变要素的投入量，即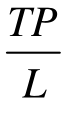。所以，平均产量就等于该点连接原点的直线的斜率。例如，对于TP曲线上的A点，直线OA的斜率就是A点的平均产量；TP曲线上通过B点连接O点所得的直线的斜率最大，即此时劳动的平均产量达到最大值。

从以上分析中可以得出三点结论：（1）总产量曲线上通过A点的切线最陡，其斜率最大，这意味着当劳动的投入量为LA时，其边际产量最高；在总产量曲线上的C点，其切线的斜率等于零，这表明当劳动的投入量为LC时，边际产量为零，总产量最大。（2）在连接原点与总产量曲线上的某一点的直线中，直线OB的斜率最大，所以在B点，平均产量最高。（3）直线OB和B点的切线重合，即两线的斜率相等，这表明在B点上，劳动的边际产量与平均产量相等^[1]。

5.可变要素使用量的合理区间

为了确定一种可变要素的合理使用量，经济学家习惯上把可变要素投入量与产量的变化分为三个阶段，如图5-3所示。

第Ⅰ阶段是劳动量从零到L1，这一阶段内，劳动的平均产量是递增的。因为劳动的边际产量均高于平均产量，显然，此时进一步扩大可变要素的投入量从而使产量扩大是有利可图的，至少到平均产量达到最高点L1时为止。也就是说，可变要素投入增加至平均产量达到最大。在此阶段，总产量和平均产量都是递增的，所以理性的生产者不会选择减少这一阶段的劳动投入量，而会继续增加劳动投入量。

第Ⅱ阶段是劳动量从L1到L2，平均产量开始递减至边际产量为零。这一阶段内，劳动的边际产量低于平均产量，但边际产量仍是正的。此时因为劳动的平均产量开始下降，但由于劳动的边际产量大于零，总产量仍然增加。劳动量为L2时，总产量达到最大。

第Ⅲ阶段是劳动量大于L2，总产量开始递减，边际产量为负。这一阶段内，劳动的边际产量小于零，此时的总产量、平均产量和边际产量都是下降的。所以理性的生产者不会选择增加这一阶段的劳动投入量，而是会减少劳动投入量。

第Ⅰ阶段内，只要生产要素的价格和产品的价格给定不变，一个有理性的生产者通常不会把可变要素的投入量限制在这一阶段内。同样地，一个有理性的生产者也不会在第Ⅲ阶段进行生产，这意味着相对于固定要素来说，可变要素的投入量过多了，即使其费用为零，增加其使用量也有害无利。在这种情况下，厂商减少其可变要素的投入量，反而会使总产量扩大。只有第II阶段，才是可变要素投入量的合理区间，在这一阶段，厂商可以投入较多的劳动获得更多的收益，避免投入过多的劳动而产生不必要的损失，存在利润最大化的可能性。当然，一个有理性的生产者究竟将其可变投入的使用量具体确定在这一区间的哪一点上，则要根据产品价格和要素价格水平而定。

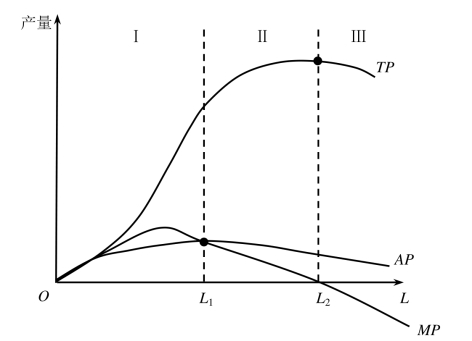
图5-3　生产的三个阶段