工期优化仅仅考虑了网络计划的时间因素，若要达到网络计划的整体最优，还必须对工期和费用进行综合优化，即计算总费用最低的工期。所谓费用优化，即以最低费用为目标来缩短工期。

1.基本概念

（1）直接费用 直接用来完成工程任务的费用称为直接费用，如直接生产人员的工资、机械设备投资、原材料费、燃料费等。直接费用直接分摊到每一项工序，欲缩短工序的持续时间，则必须为其增加必要的人力、物力等资源，因此将会引起直接费用的增加。

（2）间接费用 服务于整个工程的费用称为间接费用，如管理人员的工资、办公费、采购费、管理费等。间接费用按照工作的持续时间分摊到每一项工序，因此工序的持续时间越短，分摊到该工序的间接费用就越少。

（3）工序正常持续时间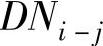初始网络计划所规定的工序持续时间。

（4）工序最短持续时间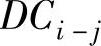工序持续时间压缩到极限程度时的持续时间。

（5）工序正常时间费用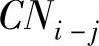利用工序正常持续时间完成工序所需直接费用。

（6）工序最短时间费用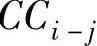利用工序最短持续时间完成工序所需直接费用。

（7）直接费用率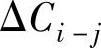将工作压缩单位时间所增加的直接费用，即：

（8）工程总费用 正常时间的工程总费用=正常时间的直接费用+正常时间的间接费用。

压缩工期后的工程总费用=正常时间的直接费用+压缩工期后增加的直接费用+压缩工期后的间接费用。

由于随着工期的缩短，直接费用增加，而间接费用减少，所以总费用为一条上凹的曲线。从而在正常工期与最短工期之间，必然存在总费用最低的工期。在该工期内完成作业，既能缩短工期，又使总费用增加最少，甚至可降低总费用。

2.费用优化步骤

1）从关键工序中选出缩短工时所需直接费用最少的方案，并确定该方案可能缩短的天数。

2）按照工序的新工时，重新计算网络计划的关键路线以及关键工序。

3）计算由于缩短工时所增加的直接费用。

不断重复上述三个步骤，直到工期不能再缩短为止。

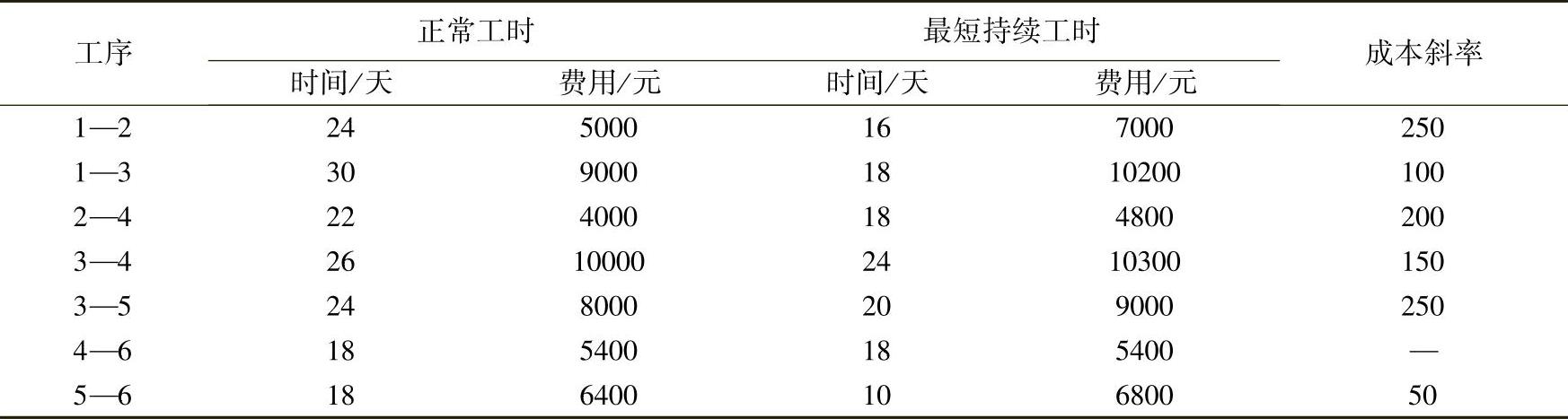
【例11.7】 已知网络计划各工序的正常工时、最短持续工时以及相应费用见表11-7，网络图如图11-16所示。

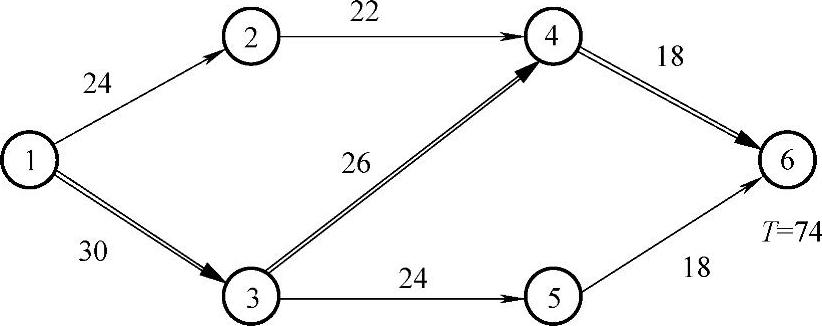
图11-16

表11-7

(www.daowen.com)

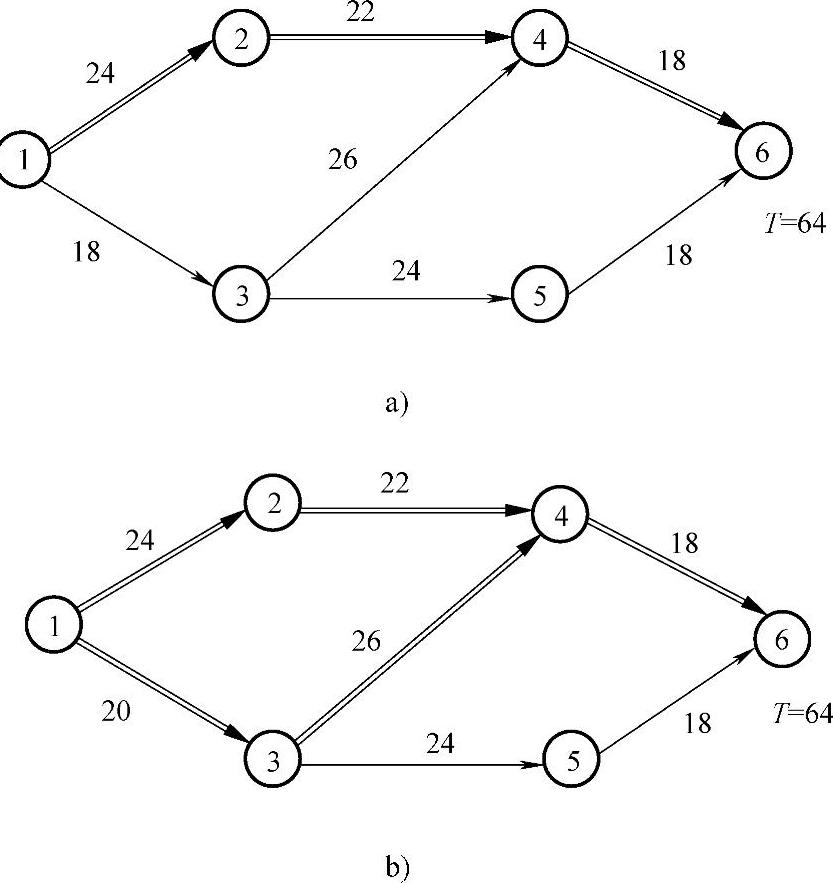
图11-17

按正常工时从图11-16中计算得到总工期为74天。关键路线为1—3—4—6，由表11-7可以计算出正常工时情况下总直接费用为47800元。

设正常工时下，任务总间接费用为18000元，工期每缩短一天，间接费用可以节省330元，求最低成本日程。

解 从图11-16可以看出，关键路线上的三道关键工序1—3、3—4、4—6中，工序1—3的成本斜率相比之下最小，应选择在工序1—3上缩短工时，查表11-7可以知道，最多可缩短12天，即取工时1—3新工时为30-12=18天。重新计算网络图的时间参数，结果如图11-17a所示，关键路线为1—2—4—6，工期为64天，实际只缩短了10天。也就是说1—3工序没有必要减少12天，1—3工时应取30-10=20天。重新计算，结果如图11-17b所示，总工期为64天，有两条关键路线：1—2—4—6与1—3—4—6，此次调整增加直接费用10×100=1000元。

重复步骤1）、2）、3），必须注意两条关键路线应同时缩短。有如下几个方案可以选择：

1）在1—3与1—2上同时缩短一天，需费用100+250=350元。

2）在1—3与2—4上同时缩短一天，需费用100+200=300元。

3）在3—4与1—2上同时缩短一天，需费用150+250=400元。

4）在3—4与2—4上同时缩短一天，需费用150+200=350元。

取费用最小方案为方案2），1—3最多可以缩短2天，2—4可以缩短4天，取其中小者，即将1—3与2—4的工时分别改为20-2=18天，22-2=20天。重新计算网络图时间参数，结果如图11-18所示。总工期为62天，这时关键路线仍为2条：1—2—4—6与1—3—4—6，增加直接费用2×300=600元。

第三次调整：选择费用最小的方案，在工序2—4与3—4上各缩短2天，即2—4与3—4的工时分别改为20-2=18天，26-2=24天，重新计算网络图的时间参数，结果如图11-19所示。总工期为60天，关键路线为：1—2—4—6、1—3—4—6和1—3—5—6，所增加的直接费用为2×350=700元。

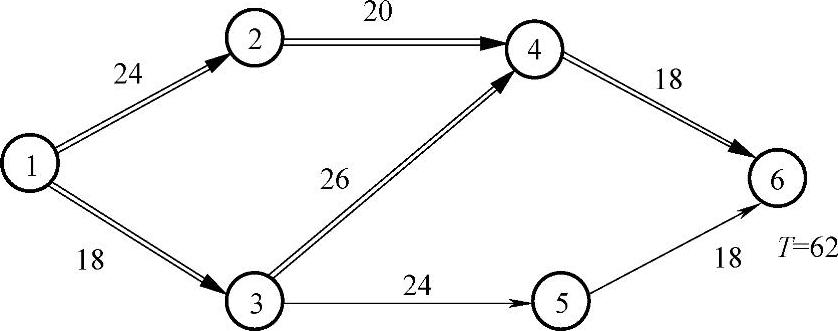
图11-18

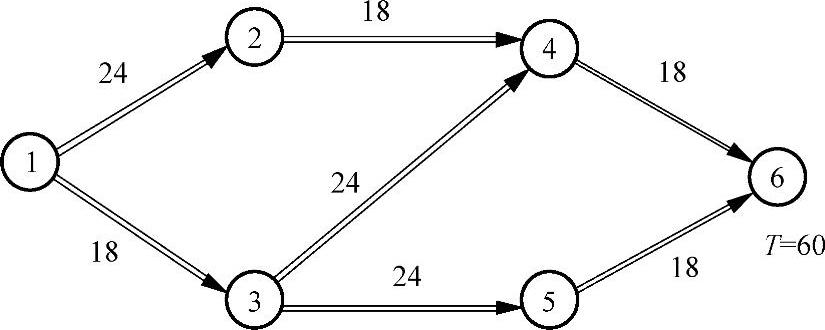
图11-19

由于一条关键路线1—3—4—6上各工序工时已经不能再缩短，所以计算结束。

全部计算过程及相应费用变化见表11-8。从表中可见，最低成本日程为62天，总成本为63440元。

表11-8

关于最低成本日程的计算步骤，也可改为计算总费用，并与上一次的总费用进行比较，直到费用不能再降低时停止计算。