工序时间是随机变量时，项目的完工期也是随机变量。设关键工序数为n，X_k为关键工序k所需时间的随机变量，则X_k相互独立，期望值和方差为

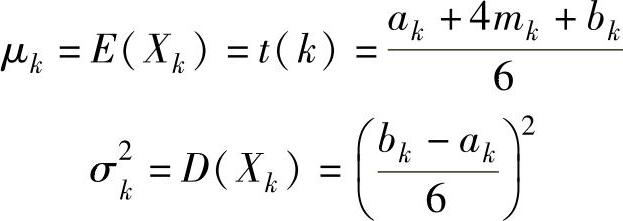
项目的完工期是一随机变量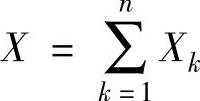，期望值和方差为

令

则由李雅普诺夫中心极限定理知

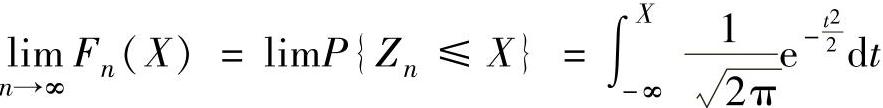
即当n很大时，Z_n近似服从N（0，1）分布，则有X=∑X_k=σ_nZ_n+μ_n近似服从N（μ_n，σ²_n）分布，即X～N（μ_n，σ²_n）。

设给定一个时间X₀，则项目完工时间不超过X₀的概率为

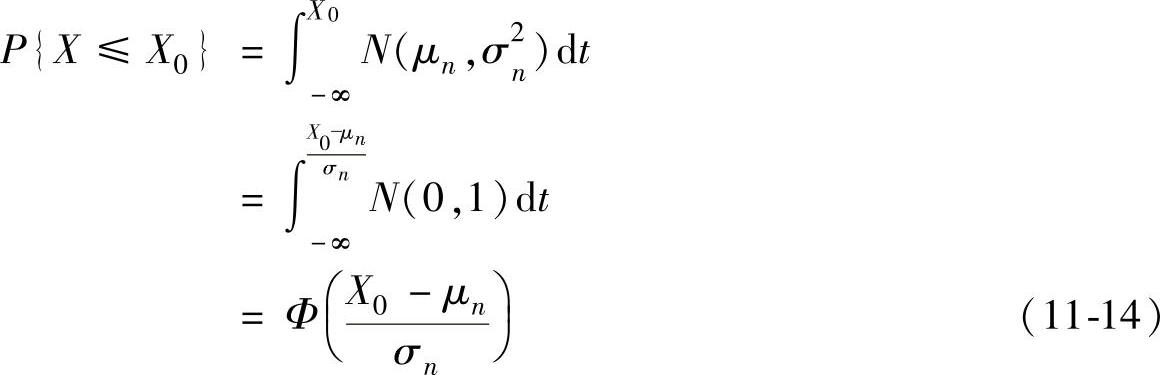
要使项目完工的概率为P₀，至少需要多少时间X₀，由

查正态分布表求出Z，又，得

X₀=Zσ_n+μ_n （11-16）当X₀=μ_n时，P=0.5

【例11.5】 根据例11.3所示的资料，完成如下问题(www.daowen.com)

1）求工序的最早开始和最迟开始时间。

2）求项目完工期的期望值及其方差。

3）求项目在72天内完工的概率。

4）要求完工的概率为0.98，至少需要多少天。

解 1）由图11-7可知，工序的最早开始和最迟开始时间如图11-11所示。

2）关键工序是c，f和j，由表11-4及式（11-12）可知，项目完工期的期望值、方差、标准差分别为

μ=12.17+23.33+33.67=69.17

σ²=0.25+1.78+2.76=4.79，σ=2.1886注意：完工期的标准差不是将各关键工序的标准差求和，而是将关键工序的方差求和后开平方。

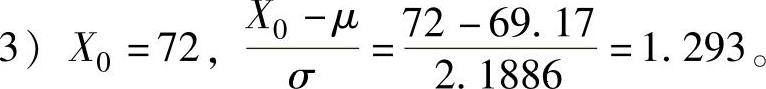
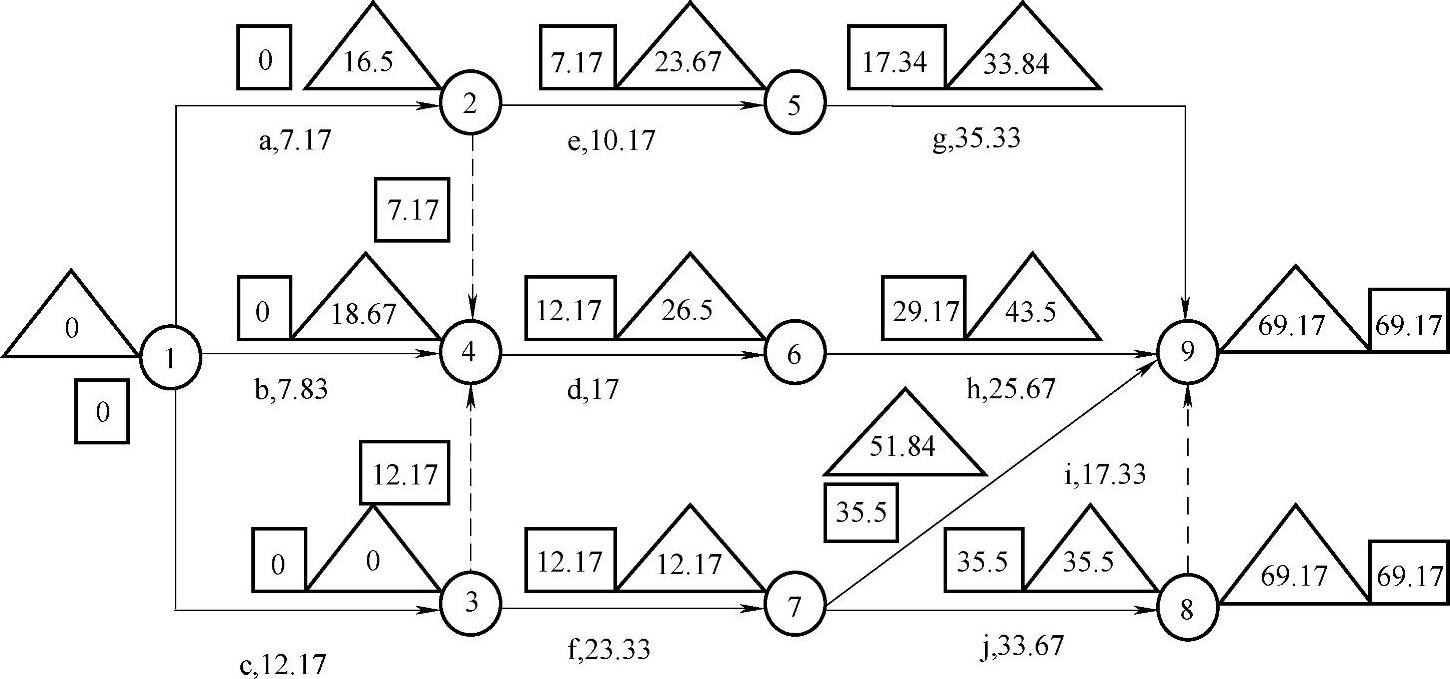
图11-11

由式（11-14），查正态分布表有：

4）已知概率P₀=0.98，由式（11-16），查正态分布表有

P{X≤X₀}=Φ（Z）=0.98，Z=2.05

X₀=Zσ+μ=2.05×2.1886+69.17=73.65（天）要使项目完工的概率为0.98，至少需要73.65天。