【例10.6】 现有赢得矩阵
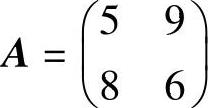
对于这个博弈而言,局中人Ⅰ能保证的最少赢得是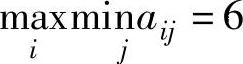 ,而局中人Ⅱ能保证的至多所失是
,而局中人Ⅱ能保证的至多所失是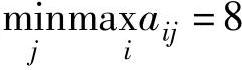 ,两者并不相等。当双方各自根据从最不利情形中选择最有利的原则选择纯策略时,应分别选择α2和β1,此时局中人Ⅰ的赢得为8,比其预期的赢得
,两者并不相等。当双方各自根据从最不利情形中选择最有利的原则选择纯策略时,应分别选择α2和β1,此时局中人Ⅰ的赢得为8,比其预期的赢得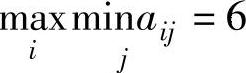 还多。原因在于局中人Ⅱ选择了β1,使局中人Ⅰ得到了本不该得到的赢得,所以策略β1对于局中人Ⅱ来说不是最优的,由此他会考虑采用β2策略。这时局中人Ⅰ会采取相应的办法,而局中人Ⅱ又会采取相应的策略来对付局中人Ⅰ的策略。这样,局中人Ⅰ采用α1和α2的可能性以及局中人Ⅱ采用β1和β2的可能性都不能排除,对于两个局中人而言,不存在一个双方都可以接受的平衡局势,即不存在纯策略意义下的解。在这种情况下,人们自然而然会想到:既然局中人没有最优策略可采用,是否可以给出一个选择不同策略的概率分布。对于局中人Ⅰ,可以制定这样一种策略:分别以概率x和(1-x)选取纯策略α1和α2,即为混合策略。同样,对于局中人Ⅱ也可以制定混合策略:分别以概率y和(1-y)选取纯策略β1和β2。解一个混合策略问题实际上就是求解两个局中人各自选取不同策略的概率分布。求解一个最优纯策略问题可以被看成求解混合策略问题的一个特例,其答案是两个局中人各自以100%的概率选取其某一个策略,而其他策略选取的概率皆为零。下面给出矩阵博弈在混合策略下的定义以及求解方法。
还多。原因在于局中人Ⅱ选择了β1,使局中人Ⅰ得到了本不该得到的赢得,所以策略β1对于局中人Ⅱ来说不是最优的,由此他会考虑采用β2策略。这时局中人Ⅰ会采取相应的办法,而局中人Ⅱ又会采取相应的策略来对付局中人Ⅰ的策略。这样,局中人Ⅰ采用α1和α2的可能性以及局中人Ⅱ采用β1和β2的可能性都不能排除,对于两个局中人而言,不存在一个双方都可以接受的平衡局势,即不存在纯策略意义下的解。在这种情况下,人们自然而然会想到:既然局中人没有最优策略可采用,是否可以给出一个选择不同策略的概率分布。对于局中人Ⅰ,可以制定这样一种策略:分别以概率x和(1-x)选取纯策略α1和α2,即为混合策略。同样,对于局中人Ⅱ也可以制定混合策略:分别以概率y和(1-y)选取纯策略β1和β2。解一个混合策略问题实际上就是求解两个局中人各自选取不同策略的概率分布。求解一个最优纯策略问题可以被看成求解混合策略问题的一个特例,其答案是两个局中人各自以100%的概率选取其某一个策略,而其他策略选取的概率皆为零。下面给出矩阵博弈在混合策略下的定义以及求解方法。
1.数学定义
【定义10.2】 设有矩阵博弈G={S1,S2,A},其中
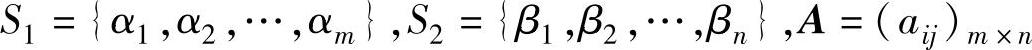
记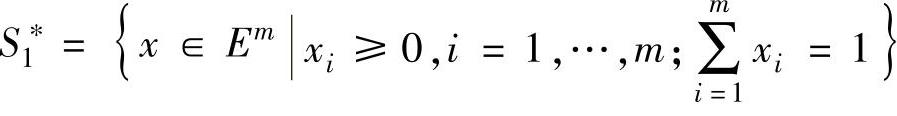
 这里,分别称
这里,分别称 和
和 为局中人Ⅰ和Ⅱ的混合策略集;记x=(x1,x2,…,xm),y=(y1,y2,…,ym),则局中人Ⅰ在选取混合策略
为局中人Ⅰ和Ⅱ的混合策略集;记x=(x1,x2,…,xm),y=(y1,y2,…,ym),则局中人Ⅰ在选取混合策略 时的赢得函数为:
时的赢得函数为:
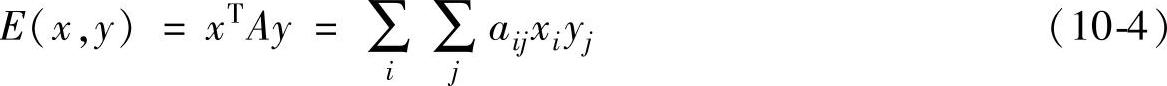
则称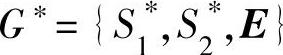 为矩阵博弈G={S1,S2,A}的混合扩充。
为矩阵博弈G={S1,S2,A}的混合扩充。
【定义10.3】 设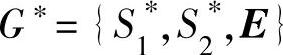 是矩阵博弈G={S1,S2,A}的混合扩充。如果
是矩阵博弈G={S1,S2,A}的混合扩充。如果
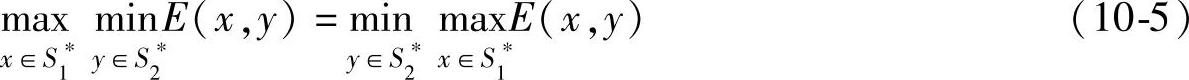
记其值为VG,即VG是博弈G={S1,S2,A}的值,称式(10-5)成立的混合局势(x∗,y∗)为G在混合策略意义下的解,称x∗和y∗分别为局中人Ⅰ和Ⅱ的最优混合策略。
以下定理给出矩阵博弈G={S1,S2,A}在混合策略意义下解存在鞍点的充要条件。
【定理10.2】 矩阵博弈G={S1,S2,A}在混合策略意义下有解的充要条件是:存在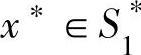 ,
, ,使
,使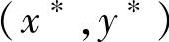 为函数E(x,y)的一个鞍点,即对一切x∗∈S1∗,y∗∈
为函数E(x,y)的一个鞍点,即对一切x∗∈S1∗,y∗∈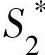
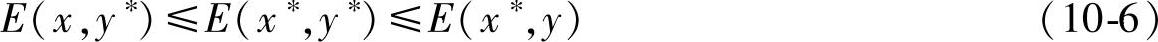
明略。【例10.7】 假设矩阵博弈G={S1,S2,A},其中:
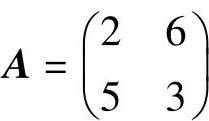
求该矩阵博弈的解。
解 该矩阵博弈不存在纯策略意义下的解。因此设x=(x1,x2)和y=(y1,y2)分别为局中人Ⅰ和Ⅱ的混合策略,则:
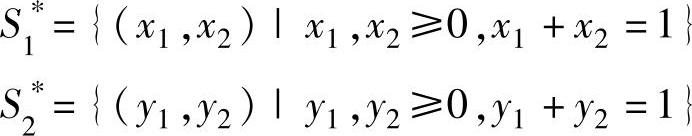
局中人Ⅰ的期望赢得值为:
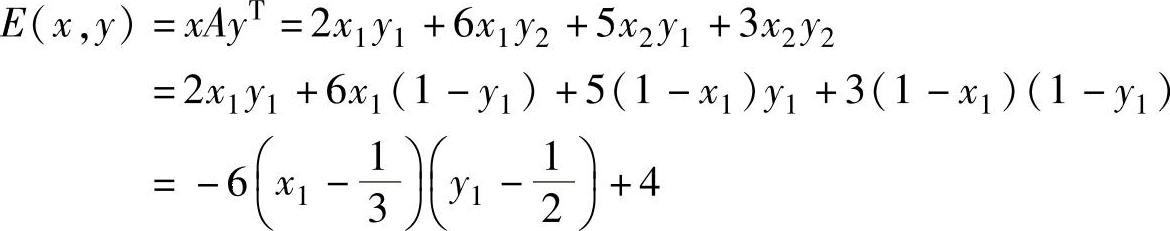
因此,取 ,
,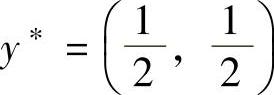 ,
,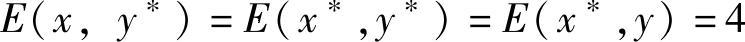 ,满足E(x,y∗)≤E(x∗,y∗)≤E(x∗,y),则
,满足E(x,y∗)≤E(x∗,y∗)≤E(x∗,y),则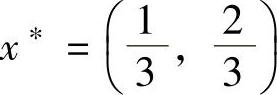 和
和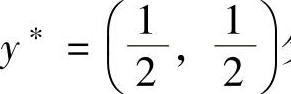 分别为局中人Ⅰ和Ⅱ的最优混合策略,即为该矩阵博弈的解,并且VG=4。
分别为局中人Ⅰ和Ⅱ的最优混合策略,即为该矩阵博弈的解,并且VG=4。
2.基本定理
本节将给出矩阵博弈在混合策略下的基本定理及其解的若干重要性质,它们在矩阵博弈的求解中起着重要作用。记

式(10-7)为局中人Ⅰ选取纯策略αi时的赢得值,式(10-8)为局中人Ⅱ选取纯策略βj时的赢得值。
由式(10-7)和式(10-8)可以得到
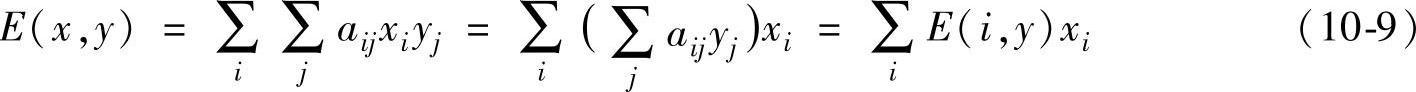
和
根据式(10-9)和(10-10),可以将式(10-6)的另一等价形式给出。
【定理10.3】 设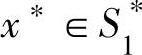 ,
,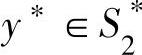 ,则
,则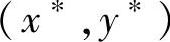 是矩阵博弈G的解的充要条件是:对任意i=1,2,…,m;j=1,2,…,n,有:
是矩阵博弈G的解的充要条件是:对任意i=1,2,…,m;j=1,2,…,n,有:
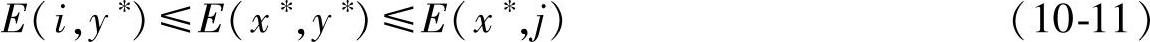
证明略。
定理10.3的等价形式是定理10.4。
【定理10.4】 设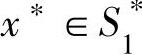 ,
,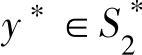 ,则
,则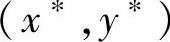 为矩阵博弈G的解的充要条件是:存在V,使得x∗和y∗分别满足(1)和(2)的解,并且V=VG。
为矩阵博弈G的解的充要条件是:存在V,使得x∗和y∗分别满足(1)和(2)的解,并且V=VG。
证明略。
【定理10.5】 对任一矩阵博弈G={S1,S2,A},一定存在混合策略意义下的解。
此定理的证明需要构造线性规划并以线性规划的相关知识进行求解,将在后面矩阵博弈的求解方法中进一步讨论。这里证明略。
【定理10.6】 设(x∗,y∗)为矩阵博弈G的解,V=VG,则:
(1)若xi∗>0,则
(2)若 ,则
,则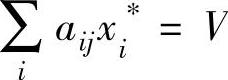 (10-14)
(10-14)
(3)若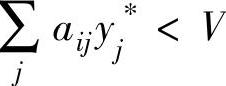 ,则xi∗=0
,则xi∗=0
(4)若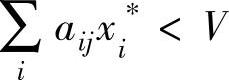 ,则yj∗=0
,则yj∗=0
若将矩阵博弈G1={S1,S2,A1}的解集记为T(G),关于博弈的解集有下列两个性质:
【定理10.7】 设有两个矩阵博弈G1={S1,S2,A1},G2={S1,S2,A2},其中A1=(aij),A2=(aij+L),L为一任意常数,则有
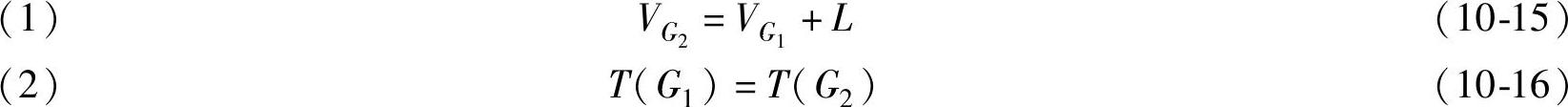
证明略。
【定理10.8】 设有两个矩阵博弈G1={S1,S2,A},G2={S1,S2,αA},其中α>0为一任意常数,则有:
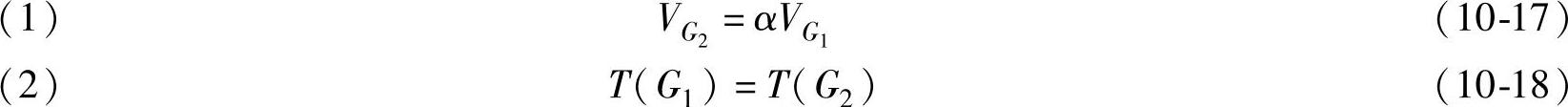
证明略。
3.矩阵博弈的求解方法
求解矩阵博弈在混合策略意义下的解的方法主要有图解法、迭代法、线性方程组法和线性规划法等。线性规划法具有一般性,并且用这种方法可以求解任意矩阵博弈。其他方法,如基于优超原则的方法、线性方程组法,均有各自适用的范围。在这里我们主要介绍线性规划法和基于优超原则的方法。
(1)线性规划法
【定理10.9】 设矩阵博弈G={S1,S2,A}的值为V,则:
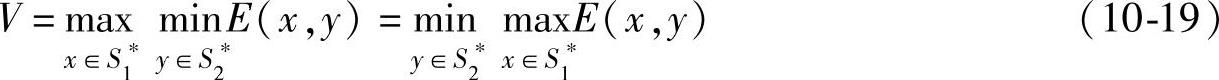
证明略。
这里,由定理10.4和10.5可知,任意矩阵博弈G={S1,S2,A}在混合策略意义下都有解,并且博弈G的解x∗和y∗等价于求解式(10-12)和式(10-13)的解。令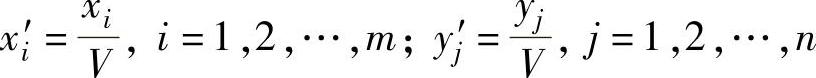
式(10-12)和式(10-13)变为:
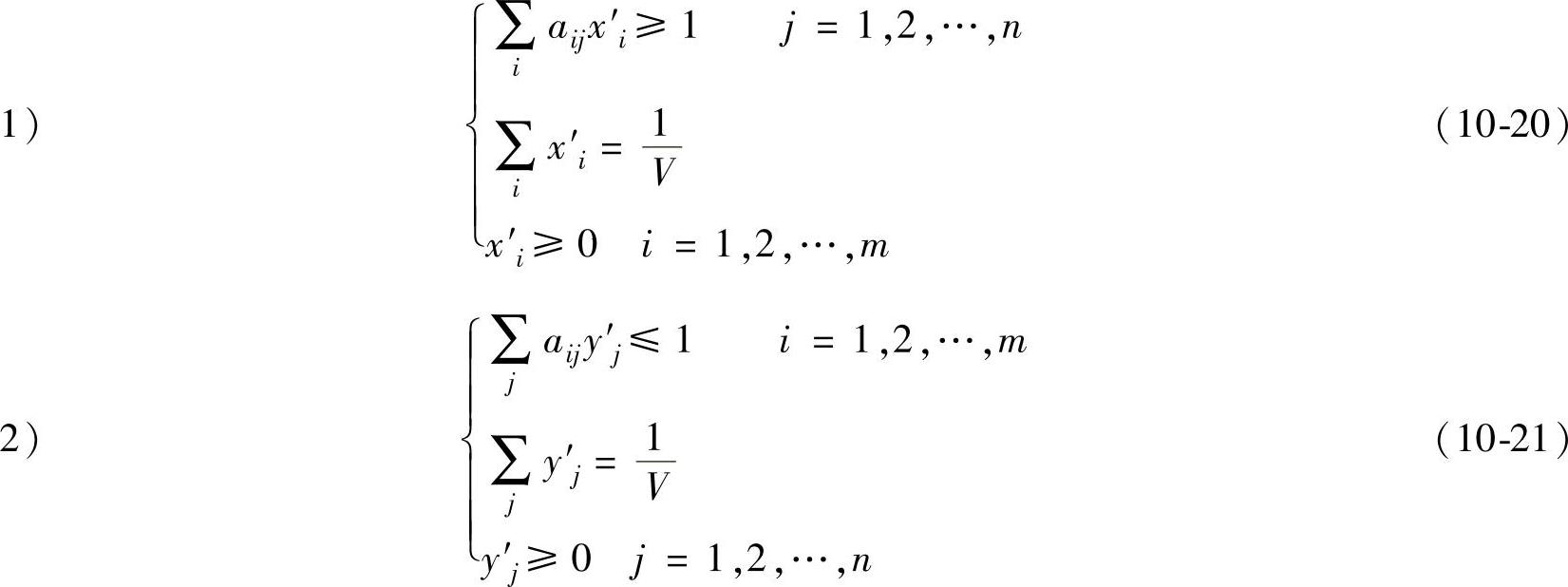
由定理10.9,对局中人Ⅰ, 等价于min1/V,式(10-20)变为线性规划问题:
等价于min1/V,式(10-20)变为线性规划问题:
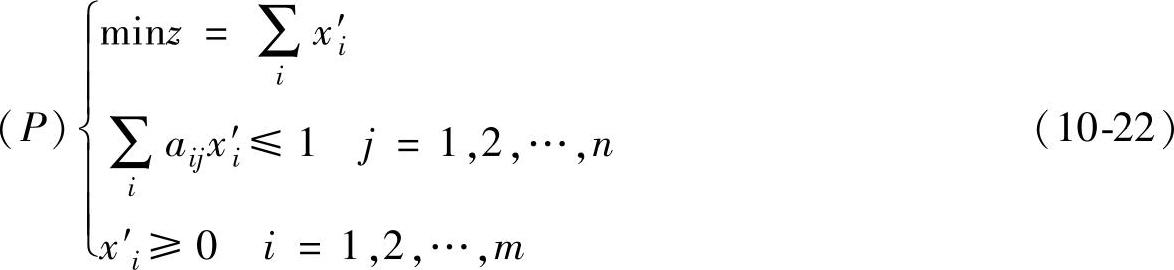
同理,对于局中人Ⅱ有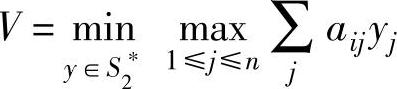 ,等价的线性规划问题为:
,等价的线性规划问题为:
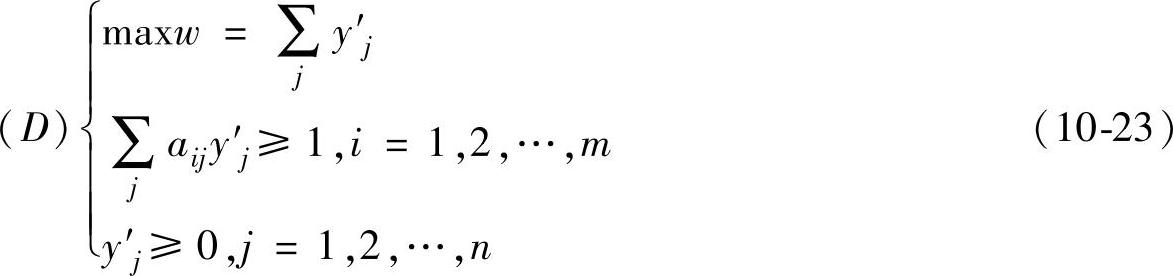
问题(P)和(D)是互为对偶的线性规划,利用单纯形法求解问题(D)或对偶单纯形法求解问题(P)。求出一个问题的最优解后,另一个问题的最优解可以从最优表中得到。再利用变换即可得到原博弈问题的解及博弈的值。
【例10.8】 两个局中人进行博弈,规则是两人互相独立地各自从1、2、3这三个数字中任意选写一个数字,如果两人所写的数字之和为偶数,则局中人Ⅱ付给局中人Ⅰ以数量为此和数的报酬;如果两人所写数字之和为奇数,则局中人Ⅰ付给局中人Ⅱ以数量为此和数的报酬,试求出其最优策略。
解 首先我们可以计算得到局中人Ⅰ的赢得值见表10-3。
表10-3 局中人Ⅰ的赢得值

可以得到局中人Ⅰ的赢得矩阵为:
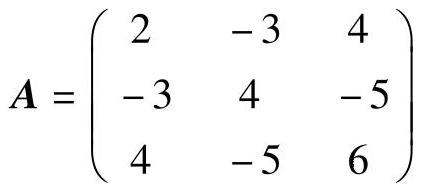
由于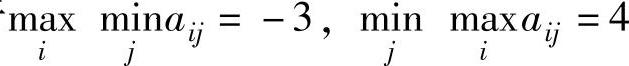 ,两者不相等。所以此博弈问题没有纯策略意义下的解,但可以求其在混合策略意义下的解,即可以求出局中人Ⅰ和局中人Ⅱ的最优混合策略。
,两者不相等。所以此博弈问题没有纯策略意义下的解,但可以求其在混合策略意义下的解,即可以求出局中人Ⅰ和局中人Ⅱ的最优混合策略。
第一步,设局中人Ⅰ采用策略α1的概率为x1,采用策略α2的概率为x2,采用策略α3的概率为x3,并设在最不利的情况下,局中人Ⅰ赢得的平均值等于V,以此建立如下数学关系:
1)局中人Ⅰ采用策略α1的概率为x1,采用策略α2的概率为x2,采用策略α3的概率为x3,三者之和为1,并可知概率值具有非负性,即:
x1+x2+x3=1,且有x1≥0,x2≥0,x3≥0
2)当局中人Ⅱ采用β1策略时,局中人Ⅰ的平均赢得为:2x1-3x2+4x3,此平均赢得应大于或等于V,即:

3)当局中人Ⅱ采用β2策略时,局中人Ⅰ的平均赢得为:-3x1+4x2-5x3,此平均赢得应大于或等于V,即:
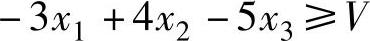
4)当局中人Ⅱ采用β3策略时,局中人Ⅰ的平均赢得为:4x1-5x2+6x3,此平均赢得应大于或等于V,即:
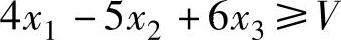
第二步,考虑V的值,V的值与赢得矩阵A的各元素的值有关。如果A的各元素的值都大于零,即不管局中人Ⅰ采用什么策略,局中人Ⅱ采用什么策略,局中人Ⅰ的赢得都是正的,这时的V值即在局中人Ⅱ采用对其最有利的策略时局中人Ⅰ的平均赢得也都是正的。因本例中所有元素均为正,因此可知V>0。但是,在更多的实际问题中,V是小于零或者等于零的数值,这时我们可以将A中的每一个元素都加上相同的一个足够大的正数K,使所得到的新的赢得矩阵A′的每一个元素都大于零。有定理能够保证这两个矩阵博弈(https://www.daowen.com)
两者的最优混合策略是相同的。因此,当求出了G′={S1,S2,A′}的最优混合策略时,也就求出了G={S1,S2,A}的最优混合策略,而且有VG=VG′-K。
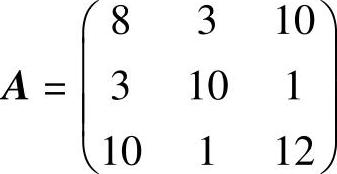
由此,为使本例的V值大于零,取K等于6,即A的各元素都加上6,得到新矩阵如下:
第三步,作变量替换,令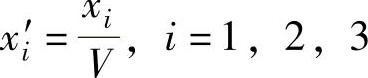 将上述关系式作变换如下:
将上述关系式作变换如下:

对局中人Ⅰ来说,他希望V值越大越好,也就是希望1/V的值越小越好,由此建立起来的关于局中人Ⅰ的最优混合策略的线性规划模型如下:
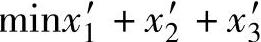
约束条件: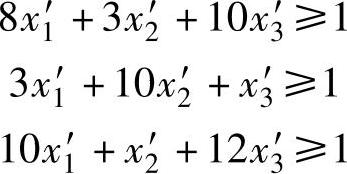

经计算求得:x1′=0.042,x2′=0.083,x3′=0.042从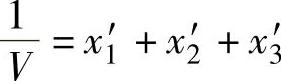 ,可以求得V=6.0
,可以求得V=6.0
再从xi=V×xi′,可以得到x1=0.251,x2=0.498,x3=0.251
由此,可以知道局中人Ⅰ的最优混合策略是以0.251的概率采用α1策略,以0.498的概率采用α2策略,以0.251的概率采用α3策略,简记为X∗=(0.251,0.498,0.251)T,V=6.0即为博弈G′的值,记为VG′=6.0,则VG=VG′-K=0。
同理可得局中人Ⅱ的最优混合策略。
设y1、y2和y3分别为局中人Ⅱ采用策略β1、β2和β3的概率,V为局中人Ⅰ采用对其最有利的策略的情况下,局中人Ⅱ损失的平均值。因此可以得到:
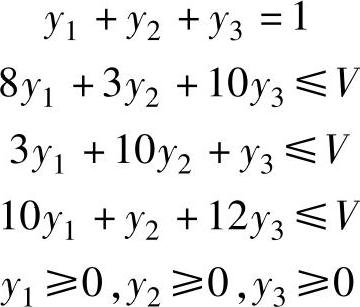
同样作变量代换,令

可以得到关系式:
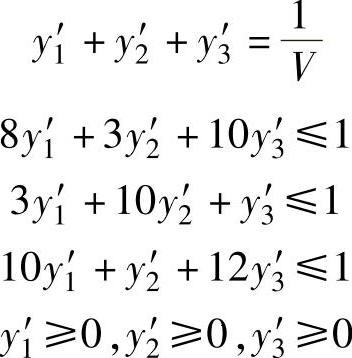
局中人Ⅱ希望损失越少越好,即V值越小越好而1/V越大越好,这样我们也建立了求局中人Ⅱ的最优混合策略的线性规划模型如下:
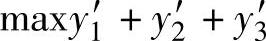
约束条件:

经单纯形法计算分别求得:
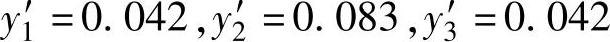
从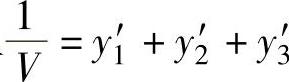 ,可以求得V=6.0
,可以求得V=6.0
再从yi=V×yi′,可以得到y1=0.251,y2=0.498,y3=0.251
由此,可以知道局中人Ⅱ的最优混合策略是以0.251的概率采用β1策略,以0.498的概率采用β2策略,以0.251的概率采用β3策略,简记为Y∗=(0.251,0.498,0.251)T,VG′=6.0,则VG=VG′-K=0。
【例10.9】 利用线性规划方法求解下述矩阵博弈,其赢得矩阵为:
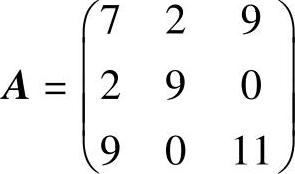
解 由于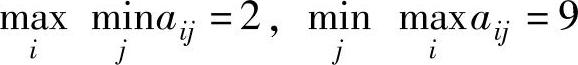 ,两者不相等。所以此博弈问题没有纯策略意义下的解,但可以求其在混合策略意义下的解,即可以求出局中人Ⅰ和局中人Ⅱ的最优混合策略。
,两者不相等。所以此博弈问题没有纯策略意义下的解,但可以求其在混合策略意义下的解,即可以求出局中人Ⅰ和局中人Ⅱ的最优混合策略。
第一步,设局中人Ⅰ采用策略α1的概率为x1,采用策略α2的概率为x2,采用策略α3的概率为x3,并设在最不利的情况下,局中人Ⅰ赢得的平均值等于V,以此建立如下数学关系:
1)局中人Ⅰ采用策略α1的概率为x1,采用策略α2的概率为x2,采用策略α3的概率为x3,三者之和为1,并可知概率值具有非负性,即:
x1+x2+x3=1,且有x1≥0,x2≥0,x3≥0
2)当局中人Ⅱ采用β1策略时,局中人Ⅰ的平均赢得为:7x1+2x2+9x3,此平均赢得应大于等于V,即:
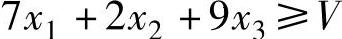
3)当局中人Ⅱ采用β2策略时,局中人Ⅰ的平均赢得为:2x1+9x2,此平均赢得应大于等于V,即:
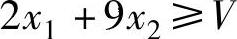
4)当局中人Ⅱ采用β3策略时,局中人Ⅰ的平均赢得为:9x1+11x3,此平均赢得应大于等于V,即:

第二步,本例中所有元素均为正,所以可知V>0。
第三步,作变量替换,令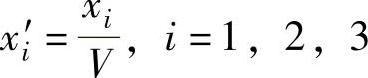 。将上述关系式作变换如下
。将上述关系式作变换如下
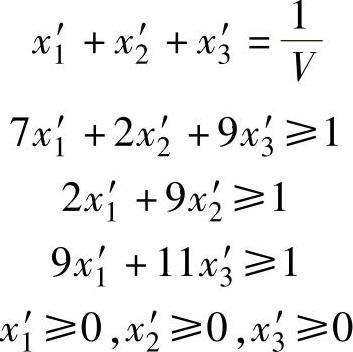
对局中人Ⅰ来说,他希望V值越大越好,也就是希望1/V的值越小越好,由此建立起来的关于局中人Ⅰ的最优混合策略的线性规划模型如下:
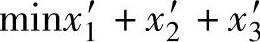
约束条件: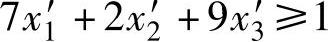
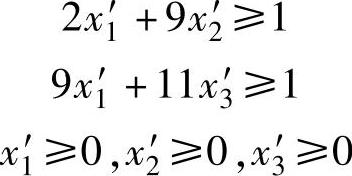
经计算求得: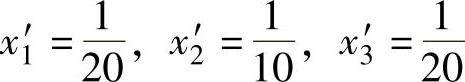 从
从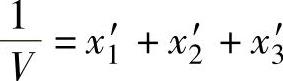 ,可以求得V=5.0再从xi=V×xi′,可以得到
,可以求得V=5.0再从xi=V×xi′,可以得到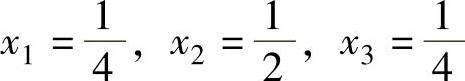
由此,可以知道局中人Ⅰ的最优混合策略是以0.25的概率采用α1策略,以0.5的概率采用α2策略,以0.25的概率采用α3策略,简记为X∗=(0.25,0.50,0.25)T,V=5即为博弈G的值,记为VG=5.0。
同理可得局中人Ⅱ的最优混合策略。
设y1、y2和y3分别为局中人Ⅱ采用策略β1、β2和β3的概率,V为局中人Ⅰ采用对其最有利策略的情况下,局中人Ⅱ损失的平均值。因此可以得到:
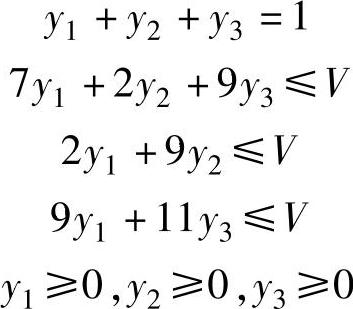
同样作变量代换,令

可以得到关系式:
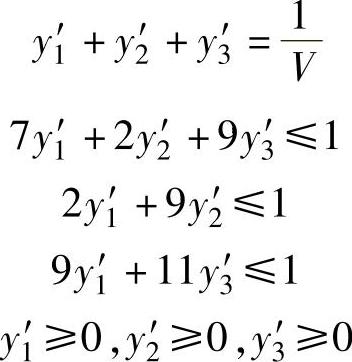
局中人Ⅱ希望损失的越少越好,即V值越小越好而1/V越大越好,这样我们也建立了求局中人Ⅱ的最优混合策略的线性规划模型如下:
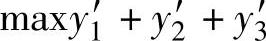
约束条件:
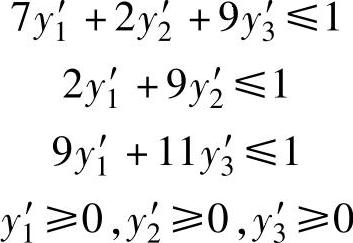
经单纯形法计算分别求得:
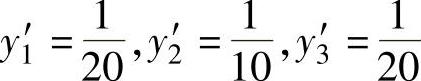
从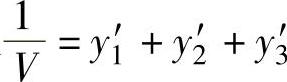 ,可以求得V=5.0再从yi=V×yi′,可以得到
,可以求得V=5.0再从yi=V×yi′,可以得到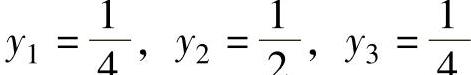
由此,可以知道局中人Ⅱ的最优混合策略是以0.25的概率采用β1策略,以0.5的概率采用β2策略,以0.25的概率采用β3策略,简记为Y∗=(0.25,0.50,0.25)T,VG=5.0。
(2)基于优超原则的解法 设A=(aij)m×n为局中人Ⅰ的赢得矩阵,如果在矩阵A中存在两行,即s行和t行,s行的元素均不小于t行的元素,即对一切j=1,2,…,n,都有:
atj≤asj称局中人Ⅰ的策略αs优超于αt,同样如果在矩阵A中存在两列,即k列与l列,k列的元素都不小于l列的元素,即对一切i=1,2,…,m都有:
ail≤aik则称局中人Ⅱ的策略αl优超于αk。
优超原则:当局中人Ⅰ的某策略αi,被其他策略之一所优超时,可以在A中划去第i行,同样对局中人Ⅱ来说,可从A中划去被其他策略之一所优超的那些列,所得的阶数较小的矩阵A′,它所对应的矩阵博弈G′与原矩阵博弈G等价,即它们有相同的矩阵博弈的解。
利用优超原则,可以简化博弈问题,下面举例说明优超原则的应用。
【例10.10】 求解矩阵博弈G={S1,S2,A},其中A为:
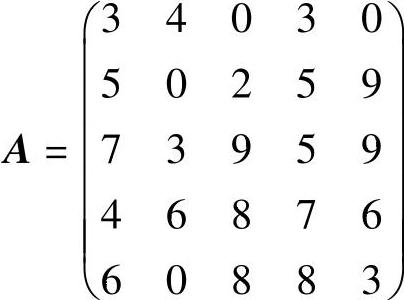
解 由于矩阵A中第4行元素均大于或等于第1行元素,所以对局中人Ⅰ而言,策略α4优超于策略α1,因此可以从矩阵A中将第1行划掉;同理,还可以将第2行划掉,得到一个新的矩阵A1:

对于A1,第1列优超于第3列,第2列优超于第4列和第5列,所以可以从A1中划掉第3列、第4列和第5列,得到矩阵A2:
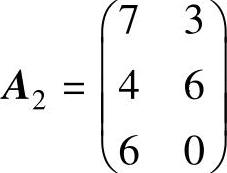
又由于A2的第1行优超于第3行,所以可以从A2中划掉第3行,得到新矩阵A3:
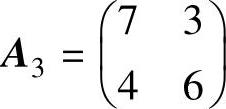
易知A3没有鞍点,由定理11.6可以求出方程组: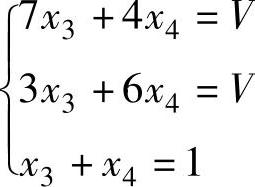 和
和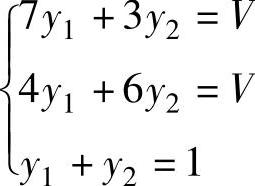 的非负解:
的非负解:
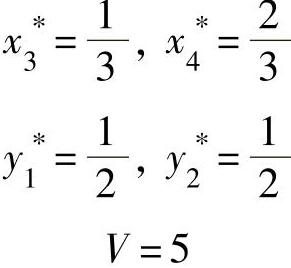
因此,该矩阵博弈的一个解为:
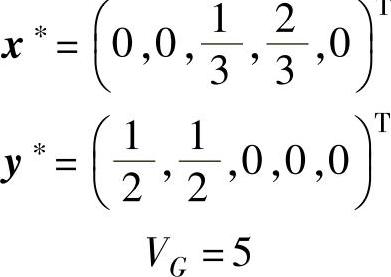
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





