矩阵博弈模型给定后，接下来对各局中人而言就是如何选取对自己最有利的策略，即求解问题。首先给出求解矩阵博弈最优纯策略的基本假设。

求解矩阵博弈最优纯策略的假设如下：

1）每个局中人对双方拥有的全部策略及当各自采取某一策略时的相互损失有充分了解。

2）对策的双方是理智的，他们参与对策的目的是力图扩大自己的收益，因而总是采取对自己有利的策略。

3）双方在相互保密的情况下选择自己的策略，并不允许存在任何协议。

下面用一个例子来分析各局中人应如何选择最有利策略。

【例10.2】 设有一矩阵博弈G={S₁，S₂，A}，其中

由A可以看出，局中人Ⅰ的最大赢得是12，要想得到这个赢得，他就得选择纯策略α₃。由于假定局中人Ⅱ也是理智的竞争者，他考虑到局中人Ⅰ打算出α₃的心理，准备以β₃对付之，使局中人Ⅰ不但得不到12，反而失掉3。局中人Ⅰ当然也会猜到局中人Ⅱ的心理，故而出α₁来对付，使局中人Ⅱ得不到3，反而失掉9……所以，如果双方都不想冒险，都不存在侥幸心理，而是考虑到对方必然会设法使自己所得最少这一点，就应该从各自可能出现的最不利的情形中选择一个最有利的情形作为决策的依据，这就是所谓的“理智行为”，也就是双方实际上可以接受的稳妥方案。

在本例中，局中人Ⅰ在各纯策略下可能得到的最少赢得分别为：-6、3、-3、-5，其中最好的结果是3。因此，无论局中人Ⅱ选择什么样的纯策略，局中人Ⅰ只要以α₂参加博弈，就能保证其赢得不少于3。同理，对局中人Ⅱ来说，各纯策略可能带来的最不利的结果是：12、3、9，其中最好的也是3，即局中人Ⅱ只要选择纯策略β₂，无论对方采取什么纯策略，他的损失值都不会超过3，而选择任何其他的纯策略都有可能使自己的损失值超过3。上述分析表明，局中人Ⅰ和Ⅱ的“理智行为”分别是选择纯策略α₂和β₂，这时，局中人Ⅰ的赢得值和局中人Ⅱ的损失值的绝对值相等，局中人Ⅰ得到了其预期的最少赢得3，而局中人Ⅱ也不会给局中人Ⅰ带来比3更多的所得，相互的竞争使博弈出现了一个平衡局势（α₂，β₂），这个局势就是双方均可接受的并且稳妥的结果。因此，α₂和β₂应分别是局中人Ⅰ和Ⅱ的最优纯策略。

这样的分析中，局中人Ⅰ是按照最小最大原则，而局中人Ⅱ是按照最大最小原则各自选取策略，所得到的（α₂，β₂）即为该博弈的解。

【定义10.1】 设G={S₁，S₂，A}为一矩阵博弈，其中：

S₁={α₁，α₂，…，αm}，S₂={β₁，β₂，…，β_n}，A=（a_ij）m×n

若

成立，记其值为V_G，则称V_G为该博弈的值，对应的策略组合（α_i∗，β_j∗）称为纯策略意义下的平衡局势，并称α_i∗和β_j∗分别为局中人Ⅰ和Ⅱ的最优纯策略。

从例10.2还可以看出，矩阵A中平衡局势（α₂，β₂）对应的元素a₂₂既是其所在行的最小元素，又是其所在列的最大元素，即有

a_i2≤a₂₂≤a_2ji=1，2，3，4 j=1，2，3，4

将此结论推广，可以得到如下定理：

【定理10.1】 矩阵博弈G={S₁，S₂，A}，在纯策略意义下有解的充要条件是：存在策略组合（α_i∗，β_j∗），使得对一切i=1，2，…，m；j=1，2，…，n，均有：

a_ij∗≤a_i∗_j∗≤a_i∗_j （10-2）对任意矩阵A，这里使式（10-2）成立的元素α_i∗_j∗称为矩阵A的鞍点。

定理10.1中式（10-2）的博弈意义是：一个平衡局势（α_i∗，β_j∗）应具有这样的性质：当局中人Ⅰ选择了纯策略α_i∗后，局中人Ⅱ为了使其所失最少，只能选择纯策略β_j∗，否则就可能失去更多；反之，当局中人Ⅱ选择了纯策略β_j∗后，局中人Ⅰ为了得到最大的赢得也只能选择纯策略α_i∗，否则就会赢得更少，双方的竞争在局势（α_i∗，β_j∗）下达到了一个平衡状态。

【例10.3】 设有矩阵博弈G={S₁，S₂，A}，其中S₁={α₁，α₂，α₃，α₄}，S₂={β₁，β₂，β₃，β₄}，并且：

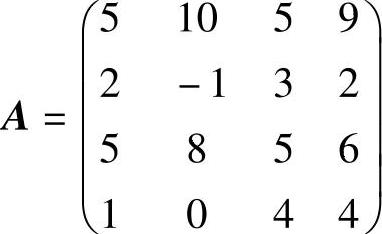(www.daowen.com)

求这个矩阵博弈的解。

解 直接在赢得表上计算有：

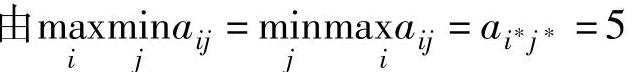，所以，（α₁，β₁）、（α₁，β₃）、（α₃，β₁）和（α₃，β₃）为该矩阵博弈在纯策略意义下的解。

【例10.4】 设有矩阵博弈G={S₁，S₂，A}，其中：

求这个矩阵博弈的解。

解 直接在赢得表A上计算有

由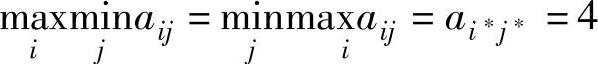，所以，（α₁，β₂），（α₁，β₄），（α₄，β₂）和（α₄，β₄）为该博弈的解。

由例10.3和10.4可知，一般博弈的解不一定是唯一的，当解不唯一时，解之间的关系具有下面两条性质：

性质1：无差别性。若（α_i1，β_j1）和（α_i2，β_j2）是博弈G的两个解，则

性质2：可交换性。若（α_i1，β_j1）和（α_i2，β_j2）是博弈G的两个解，则（α_i1，β_j2）和（α_i2，β_j1）也是G的两个解。

这两条性质表明：矩阵博弈的值是唯一的，即当一个局中人选择了最优纯策略后，他的赢得值不依赖于对方的纯策略。

【例10.5】 某货运单位采购员在秋天时要决定冬季取暖用煤的采购量。已知在正常气温条件下需要煤15t，在较暖和较冷气温条件下分别需要煤10t和20t。假定冬季的煤价随天气寒冷程度而变化，在较暖、正常、较冷气温条件下每吨煤的价格分别为100元、150元和200元。又设秋季时煤的价格为100元/t，在没有关于当年冬季气温情况准确预报的条件下，秋季时应采购多少吨煤能使总支出最少？

在本例中，采购员可以看成一个局中人，其有3个策略：在秋季时购买10t，15t或20t煤，分别记为α₁、α₂和α₃。另一个局中人可以看成环境，也有3种策略：出现较暖、正常或较冷的冬季，分别记为β₁、β₂和β₃。

现将该单位冬季用煤的全部费用（秋季购煤费用与冬季不够时再补购的费用之和）作为采购员的赢得，得到赢得矩阵如下：

表10-2 赢得矩阵

则赢得矩阵如下：

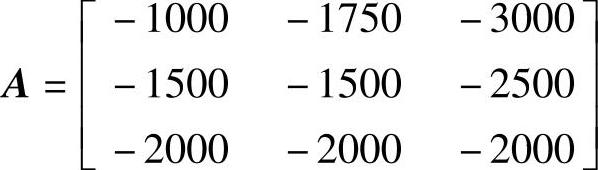
由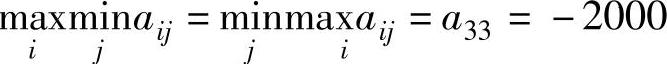可知该博弈的解为（α₃，β₃），即秋季购煤20t较好。