根据递阶层次结构就能很容易地构造判断矩阵。

构造判断矩阵的方法是：每一个具有向下隶属关系的元素（被称为准则）作为判断矩阵的第一个元素（位于左上角），隶属于它的各个元素依次排列在其后的第一行和第一列。

大多数判断矩阵填写的方法是：向填写人（专家）反复询问，针对判断矩阵的准则，其中两个元素两两比较哪个重要，重要多少，对重要性程度按1～9赋值（重要性标度值见表9-9）。

表9-9 重要性标度含义表

设填写后的判断矩阵为A=（a_ij）n×n，判断矩阵具有如下性质：

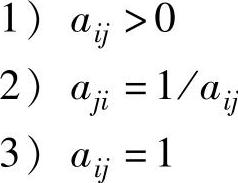
根据上面的性质，判断矩阵具有对称性，因此在填写时，通常先填写a_ij=1部分，然后再填写上三角形或下三角形的n（n-1）/2个元素即可。

在特殊情况下，判断矩阵可以具有传递性，即满足等式a_ij·a_jk=a_ik。

当上式对判断矩阵所有元素都成立时，则称该判断矩阵为一致性矩阵。

【例9.10】 交通工程建设项目决策：构造判断矩阵并请专家填写。

解 征求专家意见，填写后的判断矩阵如下：

表9-10 判断矩阵表

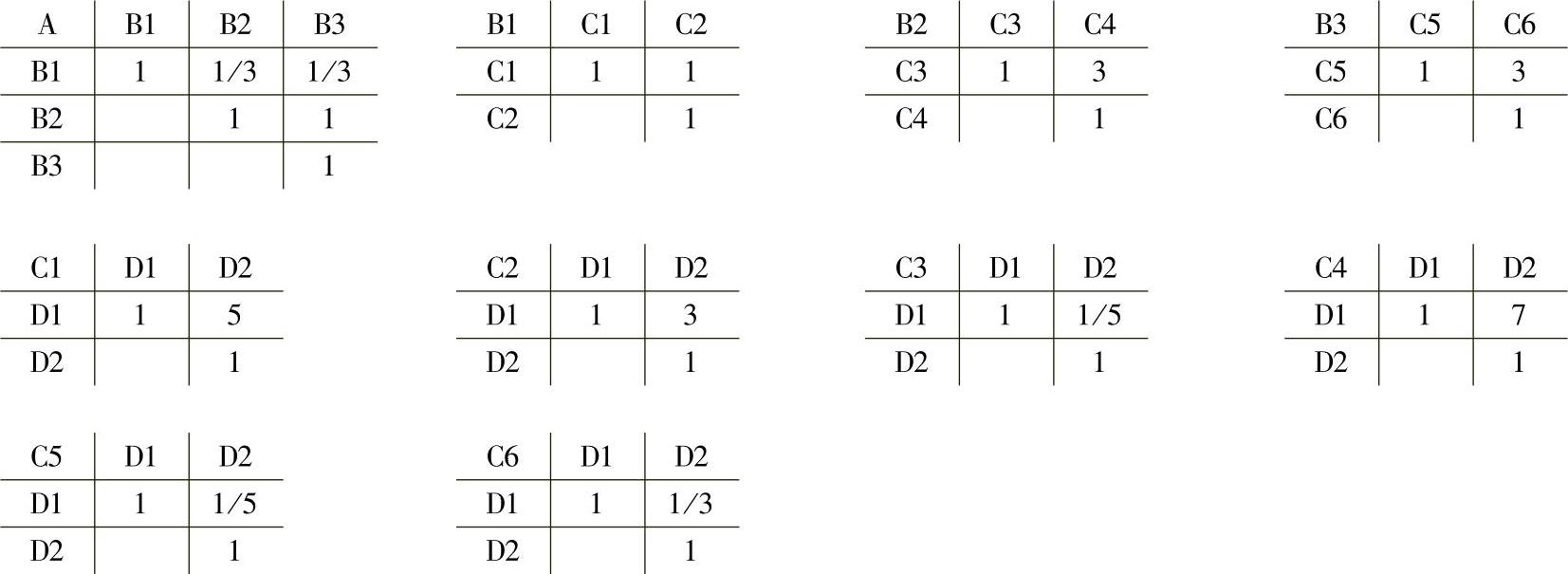
对于专家填写后的判断矩阵，利用一定数学方法进行层次排序。

层次单排序是指每一个判断矩阵各因素针对其准则的相对权重，所以本质上是计算权向量。计算权向量方法有特征根法、和法、根法、幂法等，这里简要介绍和法。

和法的原理是：对于一致性判断矩阵，每一列归一化后就是相应的权重。对于非一致性判断矩阵，每一列归一化后近似其相应的权重，在对这n个列向量求取算术平均值作为最后的权重。具体的公式是：

(www.daowen.com)

需要注意的是，在层层排序中，要对判断矩阵进行一致性检验。只有通过检验，才能说明判断矩阵在逻辑上是合理的，才能继续对结果进行分析。

一致性检验的步骤如下：

第一步，计算一致性指标C.I.（Consistency Index）

第二步，查表确定相应的平均随机一致性指标R.I.（Random Index）。

根据判断矩阵不同阶数查表9-11，得到平均随机一致性指标R.I.。例如，对于n=5阶的判断矩阵，查表得到R.I.=1.12。

表9-11 平均随机一致性指标R.I.表

第三步，计算一致性指标C.R.并进行判断

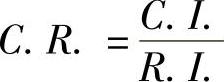
当C.R.<0.1时，认为判断矩阵的一致性是可以接受的，而当C.R.>0.1时，认为判断矩阵不符合一致性要求，需要对该判断矩阵进行重新修正。

【例9.11】 交通工程建设项目决策：计算权向量及检验。

解 上例计算所得的权向量及检验结果如下：

表9-12 层次计算单排序权向量及检验结果

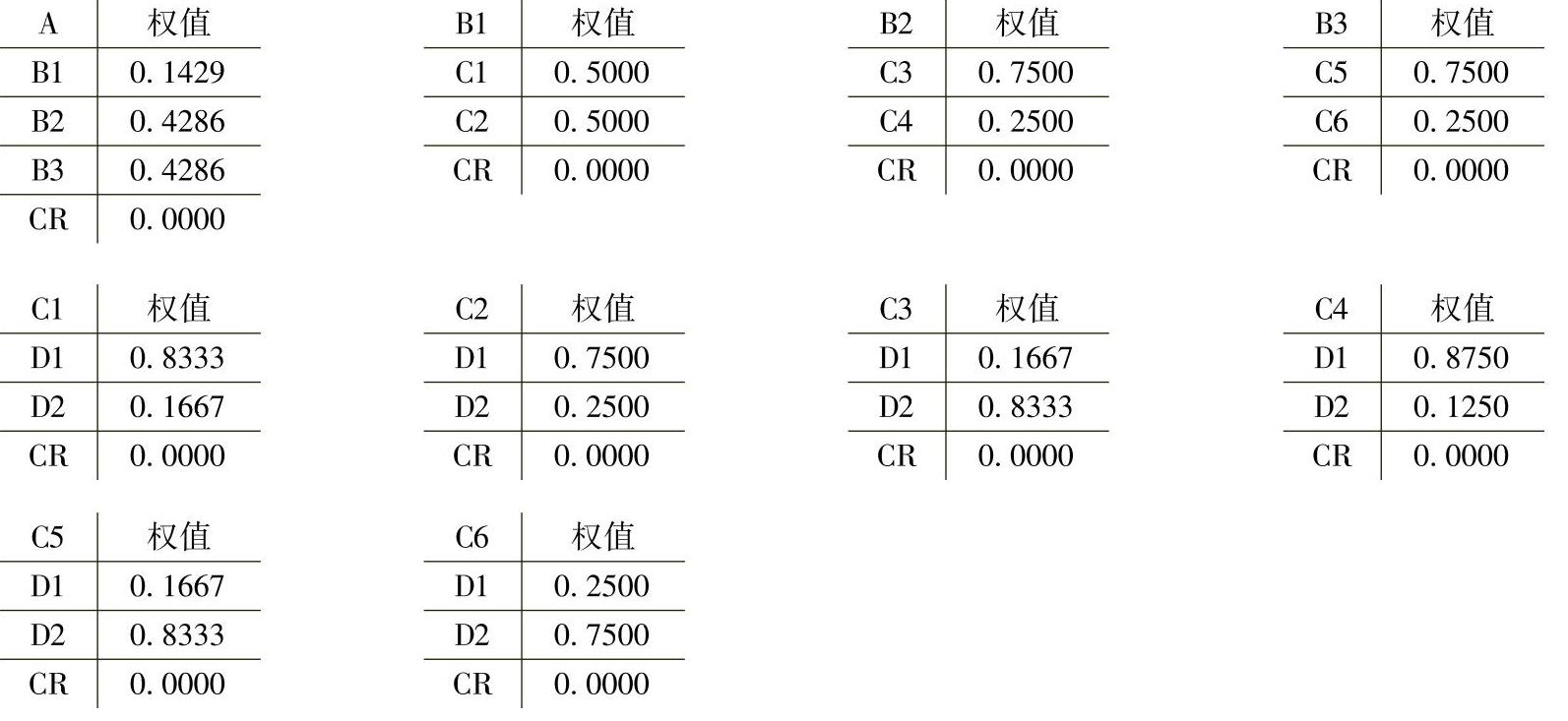
可以看出，所有单排序的C.R.<0.1，认为每个判断矩阵的一致性都是可以接受的。