风险型决策是指决策者在目标明确的前提下，对客观情况并不完全了解，存在着决策者无法控制的两种或两种以上的自然状态，但对于每种自然状态出现的概率大体可以估计，并可计算出在不同状态下的效益值，主要应用于战略决策或非程序化决策中。

风险型决策的主要特征是：

1）存在决策者希望达到的一个明确目标（收益最大或损失最小）。

2）存在两个或两个以上的自然状态。

3）出现各种自然状态的概率可以预先估计或计算出来。

4）存在可供决策者选择的两个或两个以上的行动方案。

5）不同的行动方案在不同自然状态下的效益值（或损失值）可以计算出来。

1.期望收益值法

期望收益值法是应用概率论中计算离散随机变量数学期望的方法，分别计算各种方案在各种自然状态下的期望收益值，再根据期望值的大小选出最优方案。

（1）决策步骤

1）编制决策收益值表。

2）计算每个方案的期望收益值，即：

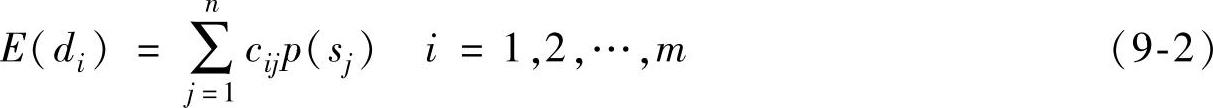
3）选择期望收益值最大的方案为备选方案，即：

（2）算例求解 仍以例9.1为例，假定货物量大的可能性是30%，货物量中的可能性是50%，货物量小的可能性是20%，求出最优决策方案。

经计算，得到期望收益值见表9-5。

表9-5 期望收益值表（单位：万元）

在本例中，对于每个方案a_i（i=1，2，3，4），有：

则d^∗=max{345，270，181，265}=345

故最优方案为a₁，建超大型仓库。

2.期望损失值法

期望损失值法要求决策者首先计算出各个方案的损失值（遗憾值），然后计算每种方案的期望损失值，选择最小期望损失值对应的方案为最优方案。

（1）决策步骤

1）编制不同方案在不同自然状态下的损失值表。

2）计算不同方案的期望损失值，即：

3）选择期望损失值最小的方案为最优方案，即：

（2）算例求解

【例9.2】 以例9.1为例，用最小期望损失值法进行决策。

计算得到期望损失值见表9-6。

表9-6 期望损失值表（单位：万元）

在本例中，对于每个方案a_i（i=1，2，3，4），有：

d∗=min{60，135，224，140}=60

故最优方案为a₁，建超大型仓库。

3.决策树方法

决策树是由决策点、事件点及结果构成的树形图，一般应用于序列决策问题中，以最大收益期望值或最低期望成本作为决策准则。决策树通过图解方式求解在不同条件下各个方案的效益值，然后通过比较做出决策。

（1）决策树的基本模型 决策树由五个部分组成：

1）决策节点。在决策树中用□表示，它代表决策者要在此处进行决策。从它引出的每一个分枝，都代表决策者可能选取的一个策略（又称方案枝）。

2）事件节点。在决策树中用○表示，从它引入的分枝代表其后继状态，分枝上括号内的数字表明该状态发生的概率（又称概率枝）。

3）结果节点。在决策树中用△表示，它表示决策问题在某种可能情况下的结果，它旁边的数字是这种情况下的益损值（又称末梢）。

4）分枝。在决策树中用连接两个节点的线段表示。根据分枝所处的位置不同，又可以分成方案枝和状态枝。连接决策节点和事件节点的分枝称为方案枝；连接事件节点和结果节点的分枝称为状态枝。

5）剪枝。在决策树中用∥表示，它代表经过比较选择此种方案被否决，称之为剪枝。

决策树的基本结构如图9-2所示。(www.daowen.com)

图9-2 决策树的基本结构

（2）决策树的基本步骤

1）画决策树。根据题意做出决策树图。

2）计算各方案的期望值。按期望值的计算方法，从图的右边向左逐步进行，并将结果表示在方案节点的上方。

3）剪枝选择方案。比较各方案的期望值，选取期望收益最大或期望损失最小的方案为最佳方案。将最佳方案的期望值写在决策点的上方，并在其余方案枝上画“∥”进行剪枝，表示舍弃该方案。

（3）算例分析

1）单级决策问题。单级决策问题是指在一个决策问题中只有一个层次的决策。反映在决策树模型中，就是只有一个决策节点。

【例9.3】 某公司投入不同数额的资金对道路进行改造。改造有三种方案，分别为修建新道路、大修现有道路和维护现有道路。根据经验，相关投入额及不同运营情况下的效益值见表9-7，请选择最佳方案。

表9-7 效益值表（单位：万元）

解 （1）画出决策树如图9-3所示。

（2）计算各方案的期望效益值：

E（2）=[0.6×25+0.4×（-20）]-15=-8

E（3）=[0.6×20+0.4×（-15）]-9=-3

E（4）=[0.6×15+0.4×（-9）]-5=0.4

故本例中，期望效益最大值是E（4），选择对应方案为维护现有道路方案，将期望效益最大值写在节点1上，并将另外两个方案剪枝。

2）多级决策问题。在序列决策中，常常需要根据阶段的不同做出不同的决策，包括两级或两级以上的决策称为多级决策问题。

【例9.4】 为生产某种地铁专用设备，某企业提出三个建厂方案：第一种方案，投资300万元建大厂；第二种方案，投资150万元建小厂；第三种方案，新建一个小厂，3年后若产品销路好再考虑扩建，扩建需追加100万元，后4年收益与新建大工厂相同。这三种方案均考虑7年经营期。据预测，在这7年经营期内，前3年该产品销路好的概率为0.7，销路差的概率为0.3；而若前3年销路好，则后4年销路好的概率为0.8，销路差的概率为0.2；若前3年销路差，则后4年销路肯定差。另外，估计每年不同规模建厂方案的效益值见表9-8，要求用决策树法确定应采用哪种建厂方案？

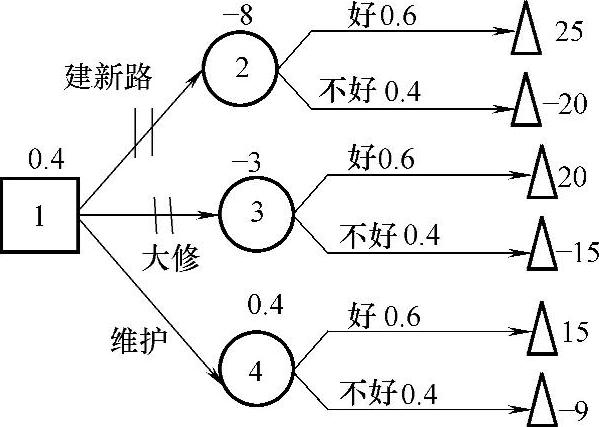
图9-3

表9-8 效益值表（单位：万元）

解 1）画出决策树如图9-4所示。

图9-4 多级决策树

2）计算事件节点的期望效益值如下：

节点5：E（5）=[0.8×120+0.2×（-30）]×4=360

节点6：E（6）=[1.0×（-30）]×4=-120

节点7：E（7）=（50×0.8+5×0.2）×4=164

节点8：E（8）=（5×1.0）×4=20

节点2：E（2）=[0.7×120×3+0.3×（-30）×3]+[0.7×360+0.3×（-120）]-300=141

节点3：E（3）=（0.7×50×3+0.3×5×3）+

（0.7×164+0.3×20）-150=80.3

由于存在二级决策点9，需要首先计算得出节点11和节点12的期望效益值，再决定是否扩建。

节点11：E（11）=[120×0.8+（-30）×0.2]×4-100=260

节点12：E（12）=（50×0.8+5×0.2）×4=164

由于节点11的期望值大于节点12，因此选取最大值对应的方案，即在决策点9上，删去不扩建方案，选择扩建方案。

接下来，分别求得：

节点9：260

节点10：（5×1.0）×4=20

节点4：（0.7×50×3+0.3×5×3）+（0.7×260+0.3×20）-150=147.5

比较各个方案，节点4的期望值最大，故节点1取最大值147.5，即先建小厂，当前3年销路好后再扩建为大厂的方案作为最终选定方案。

风险型决策问题与不确定型决策问题的本质区别在于：前者利用自然状态出现的概率分布，以期望收益值最大为决策目标，所得到的结果比较能够符合客观情况；而后者则是对未来的自然状态一无所知，其决策受主观意识的影响很大，带有一定的盲目性。

在风险型决策问题中，确定未来状态出现的概率是非常重要的。各种自然状态出现的概率，可以用统计资料、实验结果得出，但大多数情况下要凭经验、知识甚至是预感，对未来的情况进行估计，这样得出的概率值称为主观概率。对同一事件，不同的人做出主观概率的估计是不同的，因此，所得出的决策结果也不同。

对于不确定型决策，只要决策者对未来状态出现的可能性不是全然不知，就可以做出一些估计，因而即可转化成风险型的决策问题。