在不确定的情况下，决策者知道将面对的一些自然状态，也知道采用的几种行动方案在各个不同的自然状态下所获得的相应收益值，但决策者不能预先估计或计算出各种自然状态出现的概率。由于在不确定型决策中，各种决策环境并不确定，所以对于同一个决策问题，用不同的方法求解，将会得到不同的结论。决策者根据自己的主观倾向进行决策。由决策者的主观态度不同，决策准则可分为四种基本类型：悲观准则、乐观准则、折中准则和遗憾值准则。现实生活中，在进行不确定型决策的过程中，决策者的主观意志和经验判断居主导地位，同一个决策问题，决策者的偏好不同，也会使处理相同问题的方法或准则不同。

不确定型决策问题具有如下主要特征：

1）存在决策者希望达到的一个明确目标（收益最大或损失最小）。

2）存在两个或两个以上的自然状态。

3）存在可供决策者选择的两个或两个以上的行动方案。

4）不同行动方案在不同自然状态下的效益值（或损失值）可以计算出来。

【例9.1】 某货运中心需贷款修建一个仓库，初步考虑了四种规格的建库方案：①建超大型仓库a₁；②建大型仓库a₂；③建中型仓库a₃；④建小型仓库a₄。由于缺少货运中心需求量的有关背景资料，对所需货物量的多少不能事先确定，只能预先估计超大s₁、大s₂、中s₃、小s₄四种自然状态，而且每种自然状态出现的概率也无法预测。经初步估算，得到每个方案在不同自然状态下的效益值见表9-2。试求不同决策准则下决策选择方案的结果。

表9-2 效益值表（单位：万元）

1.乐观主义准则

该方法又称为极大极大决策标准，其主要特征是：实现方案选择的乐观主义原则。进行决策时，决策者不放弃任何一个获得好结果的机会，争取大中取大，充满乐观冒险精神。

（1）决策步骤

1）编制决策效益值表。2）从每一个方案中选择一个最大的收益值，即：。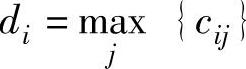

3）在这些最大的收益值对应的决策方案中，选择一个收益值最大的方案为备选方案，即：d^∗=m_iax{d_i}。

（2）决策原则 决策原则是大中取大。

（3）算例求解 在本例中，对于每个方案a_i（i=1，2，3，4，），有：

d₁=max{700，350，-200}=700

d₂=max{500，300，-150}=500

d₃=max{300，150，80}=300

d₄=max{400，250，100}=400

则d^∗=max{700，500，300，400}=700

故最优方案为a₁，建超大型仓库。

2.悲观主义准则

该方法又称为极大极小决策标准。当决策者对决策问题不明确时，唯恐由于决策失误可能带来的损失。因而，在做决策时，小心谨慎，总是抱着悲观的态度，从最坏的结果中争取最好的结果。

(1)决策步骤

1)编制决策效益值表。

2)从每一个方案巾选择一个最小的效益值，即：。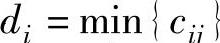

3)在这些最小的收益值对应的决策方案中，选择一个效益值最大的方案为备选方案，即：。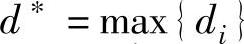

(2)决策原则 决策原则是小中取大。

(3)算例求解 在本例中，对于每个方案a_i(i=l，2，3，4)，有：

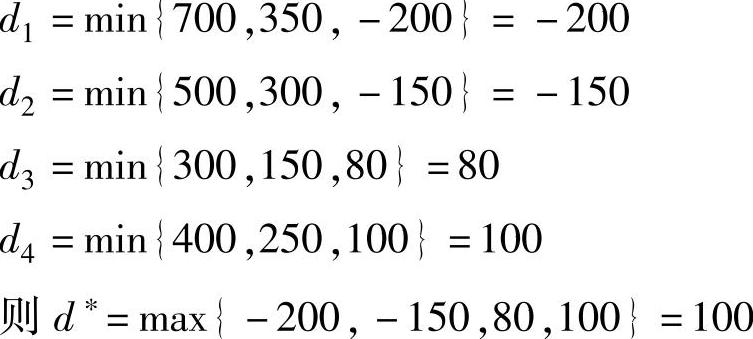
故最优方案为a₄，建小型仓库。

3.折中准则

乐观主义准则和悲观主义准则都过于极端，而折中标准是介于二者之间的一个决策标准。在进行决策的时候，要求决策者事先确定一个系数：即折中系数α，α∈[0，1]，当x→0说明决策者接近悲观，当α→1说明决策者接近乐观。

(1)决策步骤

1)编制决策效益值表。

2)计算每个方案折巾决策标准的收益值，即：(www.daowen.com)

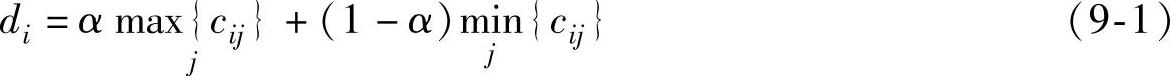
3)选择最大的折中收益值对应的方案为备选方案，即：

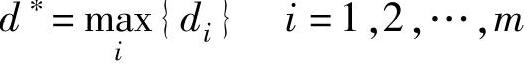
这里，当α=1时，简化为乐观主义（极大极大）准则；当α=0时，简化为悲观主义（极大极小）准则。

(2)算例求解在本例中，取折中系数α=0.6，则对于每个方案a_i(i=l，2，3，

4),有：

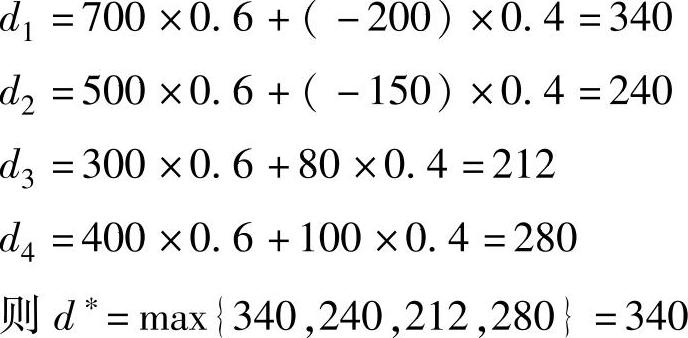
故最优方案为a₁，建超大型仓库。

4.后悔值准则或最小机会损失法

该方法是一种使后悔值最小的准则，所谓后悔值是指决策者在某种自然状态下本应选择收益最大的方案，却选择了其他方案而造成的机会损失值。该准则要求决策者首先计算各方案在不同状态下的后悔值，再分别找出各方案的最大后悔值，最后在这些最大后悔值中找出最小者，其对应的方案，即最小的最大后悔值对应的方案就作为最优决策方案。

（1）决策步骤

1）编制决策效益值表。

2）找到c_ij在自然状态下的最大收益值。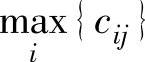

3）用每个状态下的最大收益值减去其他方案的收益值，得出每个方案的后悔值，Q_ij=。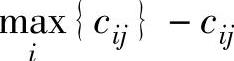

4）编制机会损失表，找出每个方案的最大后悔值，即：。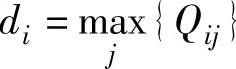

5）从每个方案的最大后悔值中找出最小的后悔值，其对应的方案即为备选方案，即：。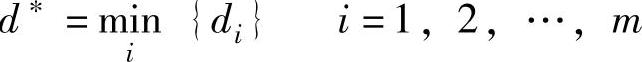

（2）算例求解 首先计算并编制后悔值表，见表9-3。

表9-3 后悔值表（单位：万元）

在本例中，对于每个方案a_i（i=1，2，3，4），有：

d₁=max{0，0，300}=300

d₂=max{200，50，250}=250

d₃=max{400，200，20}=400

d₄=max{300，100，0}=300

则d^∗=min{300，250，400，300}=250

故最优方案为a₂，建大型仓库。

5.等可能准则

该方法认为每种情况发生概率相等，均为1/m，取收益的期望值最大者为最优方案，即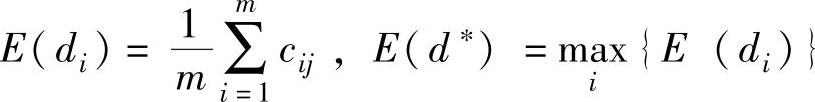。算例求解：

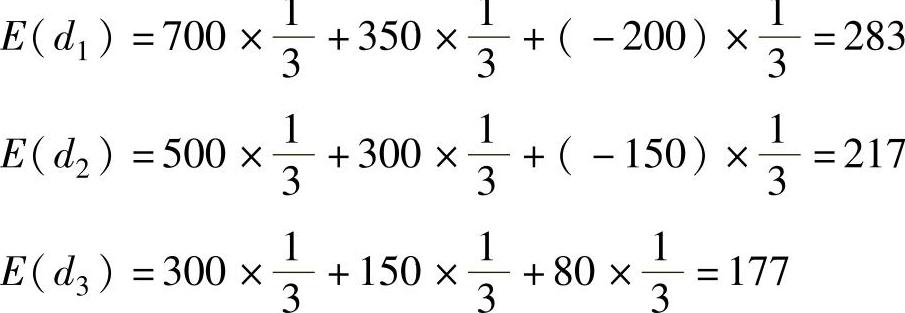
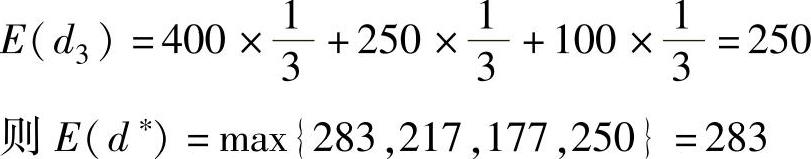
故最优方案为a₁，建超大型仓库。

上面讨论了不确定情况下的五种决策准则，具体进行决策时，可以将几个标准同时使用，选中次数最多的方案作为备选方案。

例如，在前面几个例子中，5个决策标准的决策结果见表9-4。

表9-4 不同决策标准下的决策结果

由于建立超大型仓库方案选中的次数最多，故最终应选择建立超大型仓库。