排队系统优化除了8.5.1小节中的服务率之外，还有服务台数c。事实上，当服务率提高到一定程度，就不可能再无限制地提高，这时改善排队系统服务效率的方法则应转向考虑改善服务台数。仅考虑M/M/C/∞/∞/FCFS的排队系统，其费用关系如下：

（1）服务机构的费用 这里是多服务台的服务系统，服务机构的费用是每一个服务台的单位时间费用和服务台的个数的乘积，即：

服务机构的费用=c₁c

式中，c表示服务台数；c₁表示每服务台单位时间的费用。

（2）顾客等待所消耗的费用 顾客等待所消耗的费用与8.5.1小节中相同。

（3）目标函数z 对一个完整的排队系统来说，应考虑其单位时间的费用，即服务机构的费用与顾客等待所消耗的费用之和。

（4）求解z（c）的最小值 因为c只取整数，无法使用经典的微分法，根据最小值的定义有

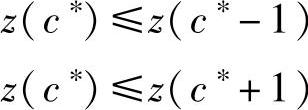
将式（8-3）中的z代入上式得

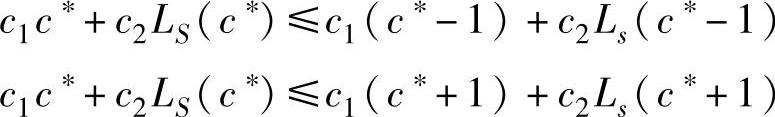
化简后可得：

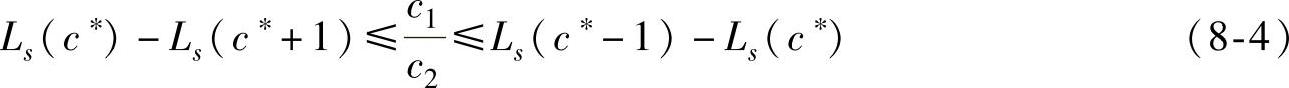(www.daowen.com)

依式（8-4），顺序求c=1，2，3…时L_s，并作相邻两个L_s之差，因c₁/c₂是已知数，根据c₁/c₂落在哪个区间，就可定出c∗。

（5）公路运输管理中的应用 以服务台数为控制变量的排队系统优化在公路运输中也是较常见的，如客运站售票窗口的设置、维修工人的定编等。这里以客运站售票窗口的设置为例，说明优化方法。

【例8.7】 某客运站，旅客到达服从泊松流，平均到达率λ=48人/h，每位旅客因排队等待而损失的费用为6元/h，售票服务时间服从负指数分布，平均服务率为25人/h，每设置1个售票窗口增加费用为4元/h（窗口早已存在，只是增加售票员而增加的补贴费用）。其他条件符合M/M/C/∞/∞/FCFS模型，问应设几个售票窗口合理？

解c₁=4元/h，c₂=6元/h

λ=48人/h，μ=25人/h

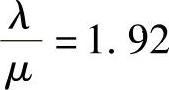
设售票窗口为c个

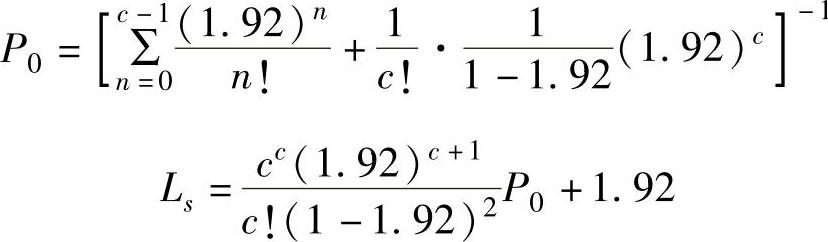
令c=1、2、3、4、5，依次代入式（8-4），得表8-4。∵c₁/c₂=0.667落在区间（0.612，18.930）内∴c^∗=3

表8-4 计算结果表

即设3个售票窗口最为合理。