（1）系统假设条件 这是单队、并列多服务台（服务台数c>1）的情况，其余条件与M/M/1/∞/∞/FCFS排队系统相同，另外规定各服务台工作是相互独立（不搞协作）且平均服务率相同，即μ₁=μ₂=…=μ_c=μ，于是整个服务机构的平均服务率为cμ，只有当1时才不会排成无限的队列。这里被称为服务强度。

（2）系统状态概率 系统状态概率这里给出公式，有关推导过程请参阅清华大学出版社出版的《运筹学》第399页。

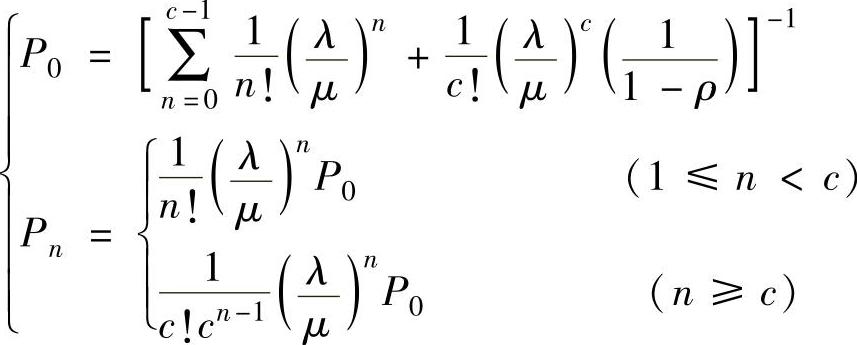
（3）系统运行指标

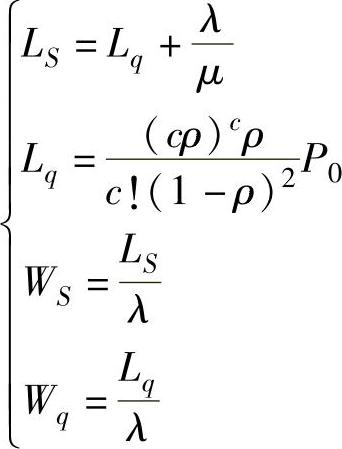
【例8.5】 某汽车性能综合监测站有3台检测设备，汽车到达速率为576辆/h，每台检测设备检测速率为240辆/h，设到达为泊松流，服务时间服从负指数分布，试求稳态概率P₀以及运行指标。

解 由已知条件知，本题可认为是M/M/C/∞/∞/FCFS排队系统。

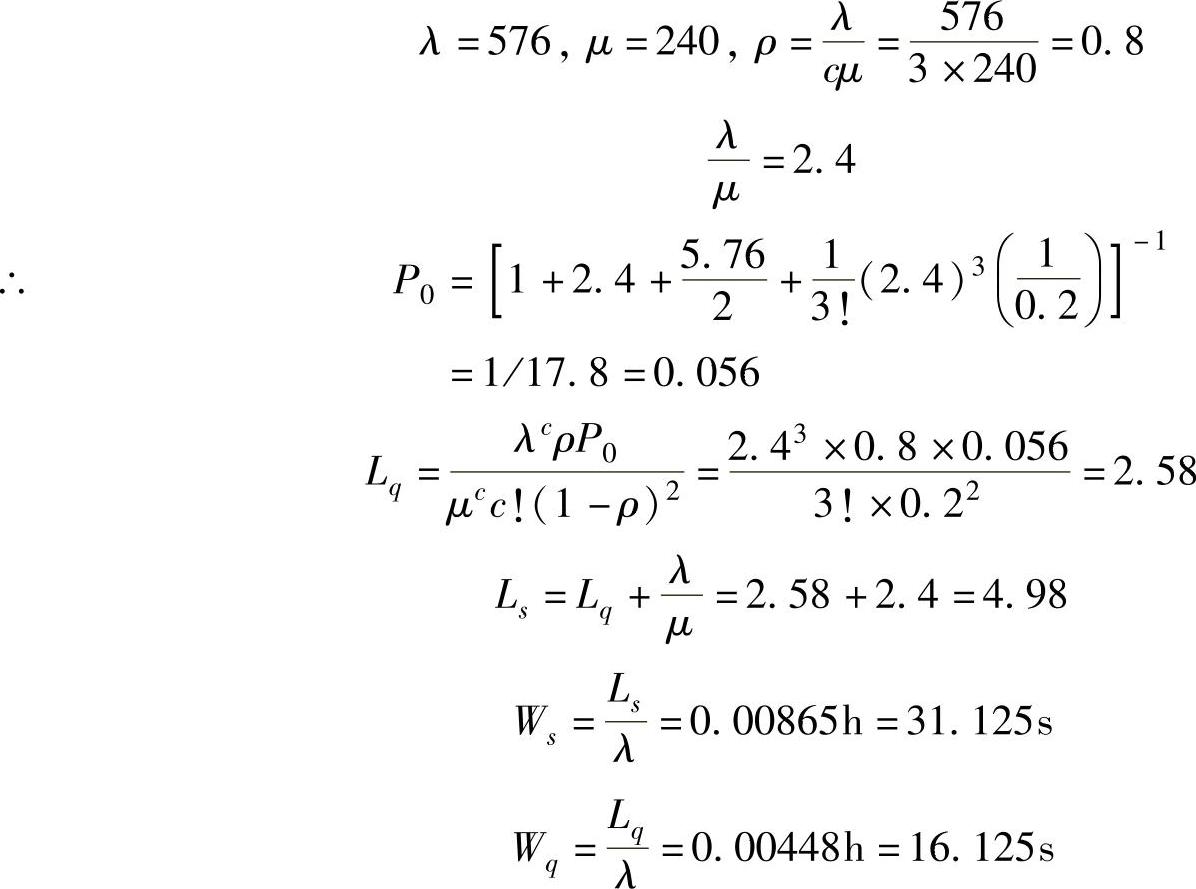(www.daowen.com)

（4）M/M/C排队系统和C个M/M/1排队系统的比较 现以例8.5的数据来说明。如果例8.5除排队方式外其他条件不变，但顾客到达后在每个窗口前各排一队且进入队列后坚持不换，结果形成3个队列，每个队列平均到达率为：

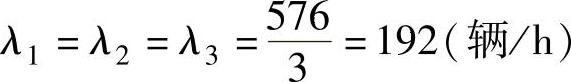
这样一来，原来的系统就变成了3个M/M/1排队系统了。

现按M/M/1排队系统解决这个问题，并与M/M/C比较，如表8-3所示。

表8-3

表中各指标对比的结果是M/M/3比M/M/1有显著的优越性。在安排排队方式时，应注意这一点。