（1）平均队长L_s（在系统中的平均顾客数，即队长期望值）

证明：依L_s的定义知：

∵0<ρ<1

故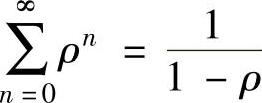

于是

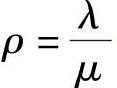∵，代入上式

得：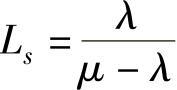

（2）平均队列长L_q（在队列中等待的顾客平均数，即队列长期望值）

证明：依L_q的定义知：

（3）平均逗留时间W_S（在系统中顾客逗留时间的期望值）

证明：顾客在系统中的逗留时间T_S是一个随机变量，它服从参数为μ-λ的负指数分布。

密度函数为：

故：

（4）平均等待时间W_q（在队列中排队等待时间的期望值）

证明：在队列中排队等待时间的期望值应等于在系统中逗留时间的期望值减去服务时间的期望值，而服务时间的期望值为1/μ。故：

（5）忙期期望值B_s

说明：系统处于繁忙状态，就意味着必须等待，而不能立即被服务：

系统处于空闲状态的概率：P₀=1-ρ

系统处于繁忙状态的概率：P（N>0）=ρ(www.daowen.com)

忙期和闲期总是交替出现的，当考虑充分长的时间，它们的期望个数总是相同的，在相当长的时期内，可以认为忙期和闲期总长之比也是ρ∶（1-ρ），于是可以认为各忙期的平均长度B_s与各闲期的平均长度I_s之比也是ρ∶（1-ρ）。但各闲期的平均长度I_s在到达间隔服从负指数分布的条件下是1/λ，故各忙期的平均长度为：

而一个忙期所服务的顾客平均数为：

现将上述几个主要运行指标归纳如下：

它们之间的相互关系为：

【例8.1】 汽车过境检查，到达平均速率为100辆/h，是泊松流；检查一辆车平均需要15s，为负指数分布，试求稳态概率P₀、P₁、P₂和系统中汽车数的期望值L_s，排队等待的汽车数的期望值L_q，过境检查全部时间的期望值W_s，等待检查时间的期望值W_q。

解 由给定条件，λ=100辆/h

【例8.2】 有一汽车冲洗站，要求冲洗的汽车按平均每1h 5辆的泊松分布到来，冲洗一辆汽车所需时间服从均值为10min的负指数分布。

试求：

1）平均队列长L_q。

2）为了估计等候冲洗的汽车的停留场地，按L_q的值进行准备是不够的，为什么？为保证每辆汽车的到来能有80%的概率有场地停放，问服务站前应准备几个停车位？

解 由已知条件，λ=5辆/h

2）仅按L_q的值进行准备是不够的，因为L_q只描述了排队等待的队列中汽车平均数，不能反映其他信息，如平均队列长的概率，平均等待时间等因素。

设有S个停车位，能保证汽车到来有80%的概率进入站内。

两边取对数并整理得：

S≥6.8≈7（辆）

可知S≈2L_q

另外，顾客在系统中期望等待时间，也是衡量冲洗台是否方便的重要因素之一，W_q=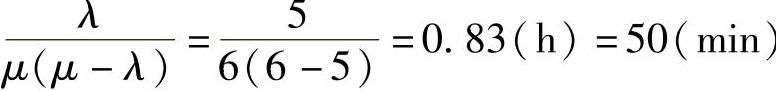，这显然太长了。