为了便于说明问题,这里介绍一种生灭过程。假设有一堆细菌,每个细菌在时间Δt内分裂成两个的概率为λΔt+O(Δt),在Δt时间内细菌死亡的概率为μΔt+O(Δt),各个细菌在任何时间段内分裂和死亡都是独立的,并且把细菌的分裂和死亡都看成一个事件的话,则在Δt时间内发生两个或两个以上事件的概率为O(Δt)。假设已知初始时刻细菌的个数,问经过时间t后细菌将变成多少个?如把细菌的分裂看成一个顾客接受完服务后离去,则生灭过程恰好反映了一个排队服务系统的瞬时状态N(t)将怎样随时间t而变化。
当有一个新顾客到达时,系统将由某一低状态转移到相邻的高状态,如由状态i转移到i+1,当有一顾客因接受完服务而立即离去时,系统将由某一高状态转移到相邻的低状态,如由状态i转移到状态i-1。系统状态转移可用图8-3表示(状态转移图)。

图8-3
其中节点编号i表示系统所处的状态,i=0,1,2…,箭头方向表示状态转移方向。
要求系统瞬时状态N(t)的概率分布是十分困难的,下面仅就系统处于稳态时的概率给以讨论。这时,对任意状态i,到达该状态的顾客平均到达率应该等于离开该状态的顾客平均离去率,即流的守恒定律。把所有各节点的状态平衡方程列表,见表8-1。
表8-1 生灭过程的状态平衡方程

例如,对第i个状态,到达该状态有两个可能性,一是来自i-1,平均到达率λPi-1,另一个是来自i+1,平均到达率μPi+1,离开该状态也有两个可能性,一是到i+1去,平均离开率λPi,另一是到i-1去,平均离开率μPi,根据守恒定律:(https://www.daowen.com)
λPi-1+μPi+1=(λ+μ)Pi(i=1,2…)
由表8-1可见,第一个方程有两个未知数P0和P1,第一和第二两个方程有3个未知数P0、P1和P2,……,未知数个数始终比方程个数多一个。因此不能直接求出所有未知数,只能得到一组递推关系。
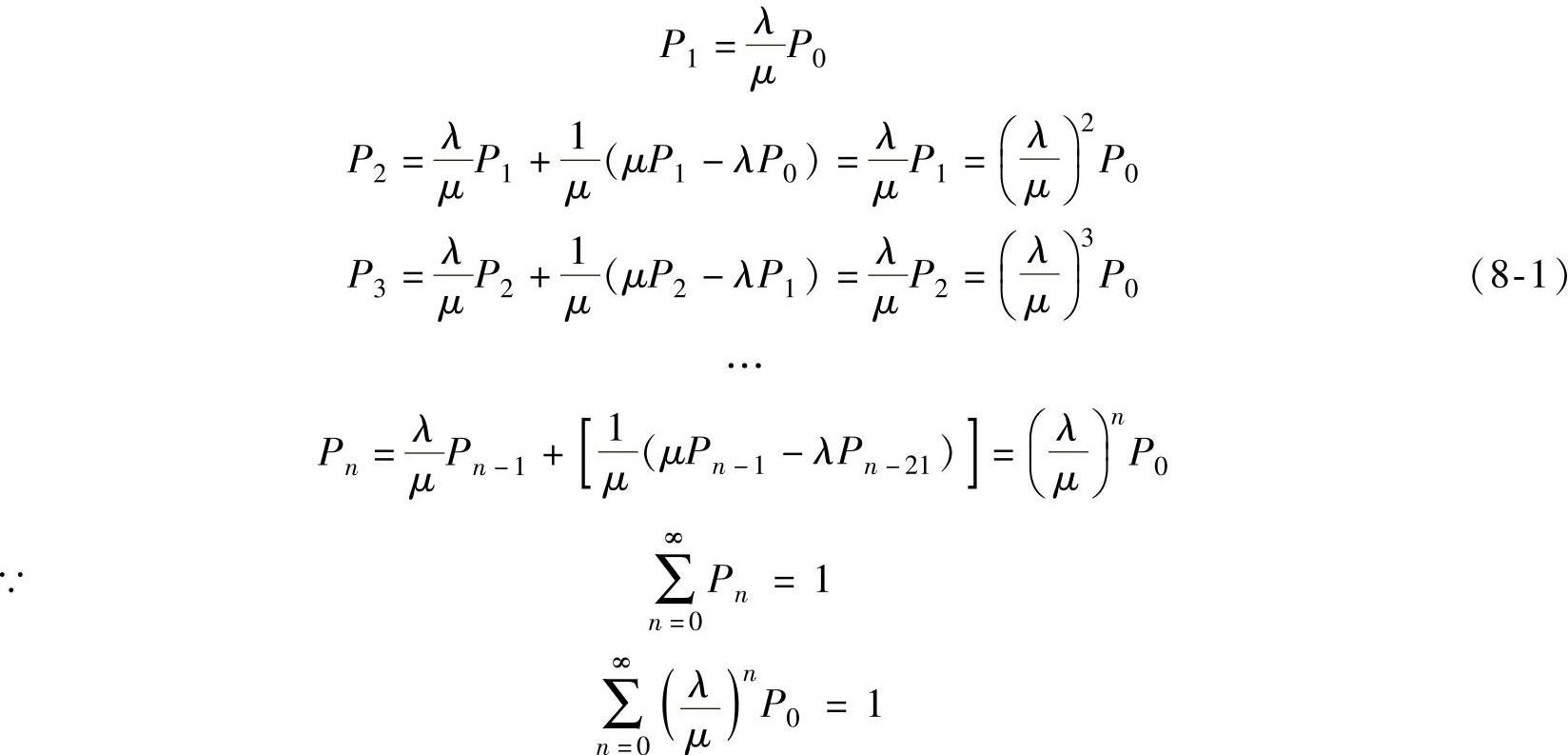

今设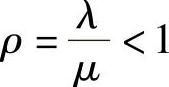 (否则队列将排至无限远),则等比级数:
(否则队列将排至无限远),则等比级数:
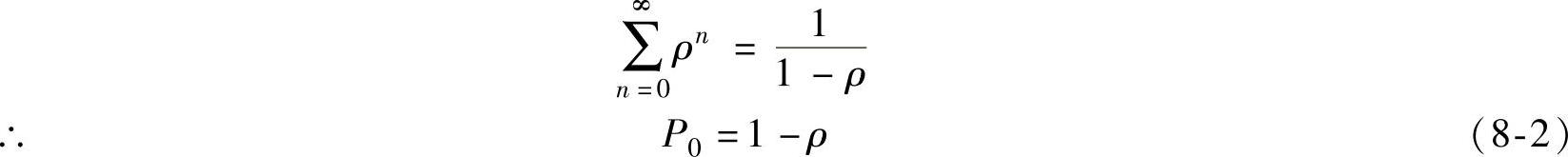
把式(8-1)和式(8-2)合并,得出系统稳态概率分布为:
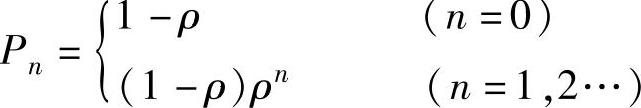
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






