【例7.11】 综合运输中交通运输方式的确定问题。如图7-30所示，将货物从A城市运送至E城市，途径B、C、D三个城市，而且每两个城市之间有三种运输方式可以选择：铁路、公路及航空。现假设运量为10个单位，图中数字1、2和3分别代表三种不同的运输方式，即铁路、公路和航空，每条边上的数字表示费用，如B2到C3表示B城市到C城市采用航空运输方式的费用为22，试求使总的运输费用最小的运输方式。

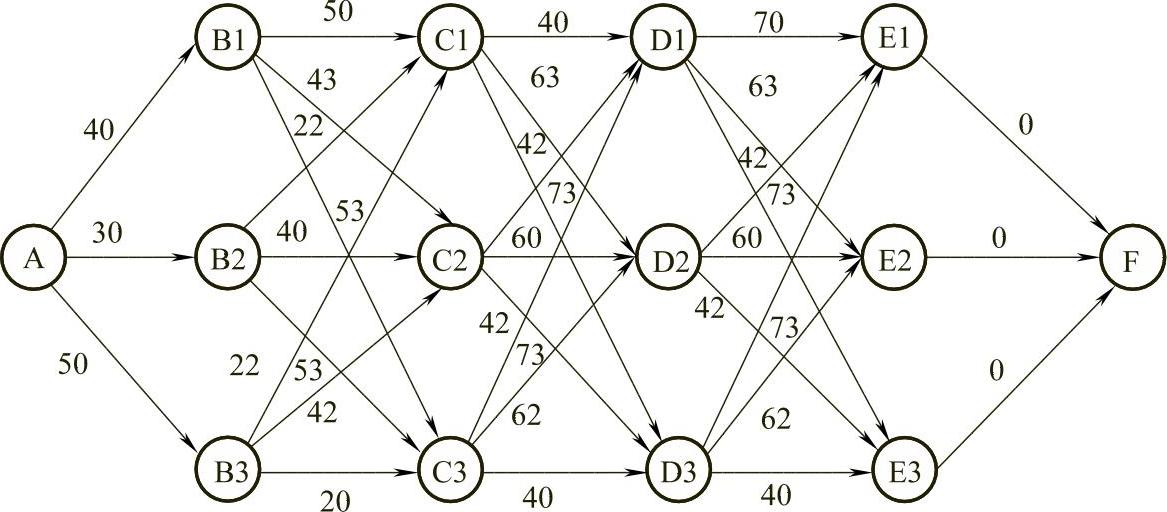
图7-30

解 由前面介绍的求解最短路的方法可求得A城市到E城市的最短路径为A→B2→C3→D1→E3→F，由此可计算得到其最小总费用为：

30+22+43+42=137即从城市A到城市B选择公路，从城市B到城市C选择航空，从城市C到城市D选择铁路，从城市D到城市E选择航空。

【例7.12】 路面更新问题。某新建公路设计年限为20年，道路使用若干年后，路面需更新。现把设计年限分成四个时期，每个时期为五年。由于各个时期路面的损坏情况不同，故各个时期的路面更新费用不一样，如图7-31所示，v_i表示“第i个时期末路面更新一次”的状态。v₀表示道路刚建成的状态，v₄表示道路到达设计年限的状态（这时路面不再更新）。节点间连线上的数字表示各状态之间的路面更新费用、养护费用及附加费用的总数，单位千元/km。如v₁→v₃连线上的数据为108，表示路面在第5年末更新后从第6年初到第15年末路面再更新一次这段时间内的总费用。

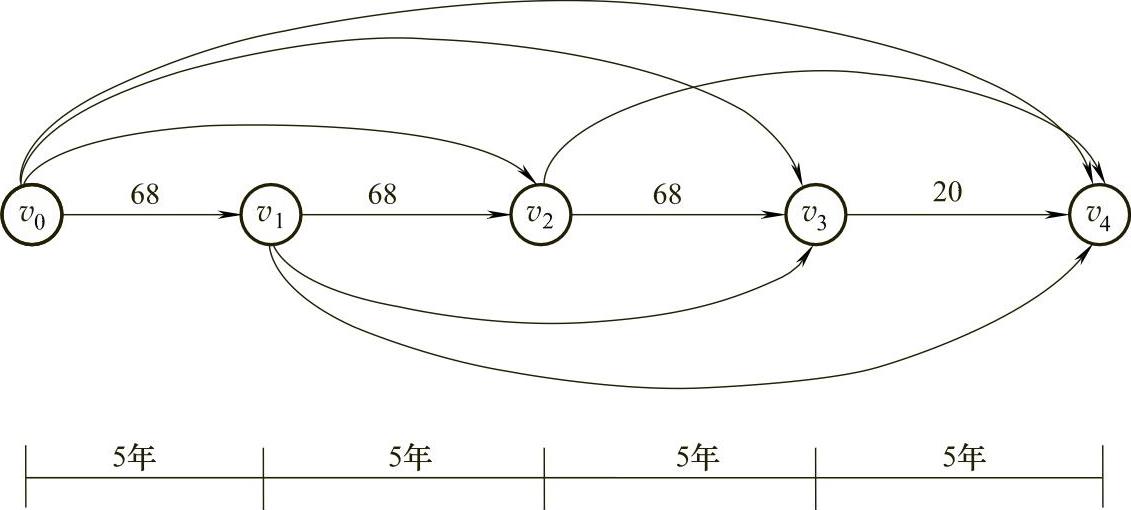
图7-31

解 可用前面介绍的求解最短路的方法求解该问题，但由于该图所示网络比较简单，用枚举法即可求出最短路，其最短路为v₀→v₂→v₄，最小总费用为：

108+52=160千元/km

即在该道路的使用年限内，第10年末更新一次路面，其总的费用为最少。

【例7.13】 服务网点设置。以图7-11为例，现提出这样一个问题，在交通网络中建立一个快速反应中心，应选择哪一个城市最好。

解 针对图7-11只有两点间的距离，可以采用“使最大服务距离达到最小”为标准，计算步骤如下。

第一步，利用Floyd算法求出任意两点之间的最短距离表（见表7-3）。

第二步，计算最短距离表中每行的最大距离的最小值，即：

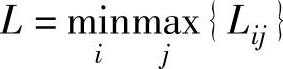
L所在行对应的点就是最佳服务点，也称为网络的中心。

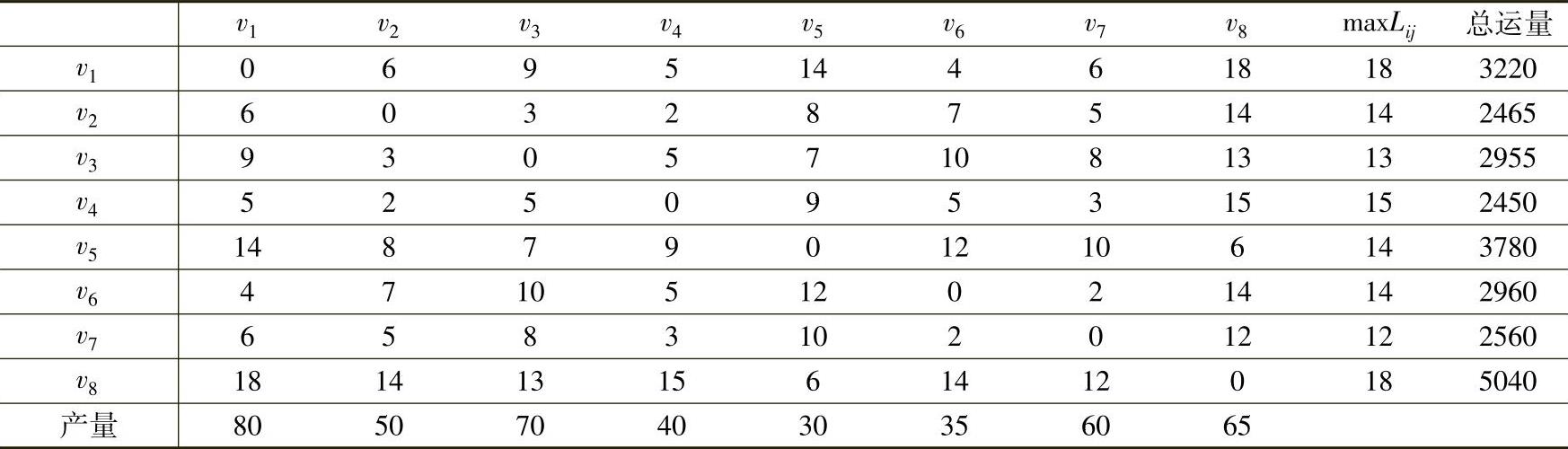
引用例7.5计算的结果，对表7-3每行取最大值再取最小值，见表7-8倒数第二列。(www.daowen.com)

表7-8中倒数第二列最小值为12，位于第七行，则v₇为网络的中心，最佳服务点应设置在v₇。

如果每个点还有一个权数，例如一个网点的人数、需要运送的物质数量、产量等，这时采用“使总运量最小”为标准，计算方法是将上述第二步的最大距离改为总运量，总运量的最小值对应的点就是最佳服务点。

表7-8中最后一行是点v_j的产量，将各行的最小距离分别乘以产量求和得到总运量，见表7-8最后一列，最小运量为2450，最佳服务点应设置在v₄。

表7-8

【例7.14】 路网最大通行能力确定问题。已知某实际交通网络如图7-32所示，弧旁的数据（c_ij，f_ij）分别表示该路段的通行能力和可行流，单位为1000辆/日，试求该路网的最大通行能力。

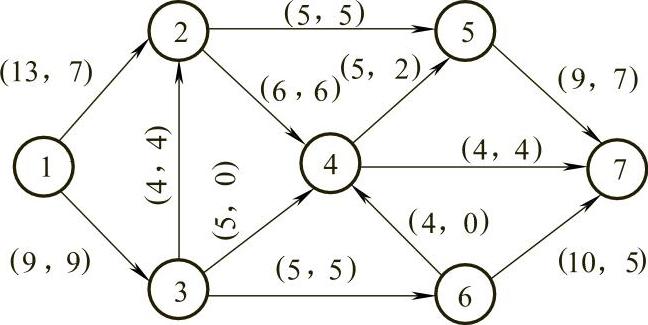
图7-32

1）用Ford-Fulkerson标号法的第二步求出另一个初始可行流，如图7-33所示。

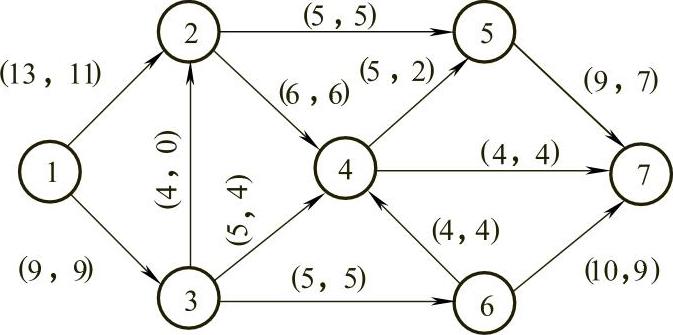
图7-33

2）标号寻找增广链。发点标号（0，∞），v₁和v₃点不满足标号条件，v₂满足标号条件，给v₂标上（v₁，2）。

检查v₂，因为在前向弧（v₂，v₅）、（v₂，v₄）上，f₂₄=c₂₄，f₂₅=c₂₅。在后向弧（v₂，v₃）上，f₃₂=0，均不满足标号条件，因此标号过程无法继续下去，即已经不存在增广链，算法结束，这时的可行流就是最大流。最大流量为：

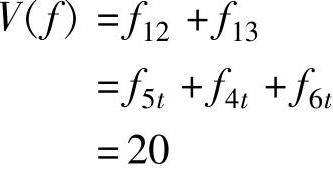
即该交通网络的最大通行能力为20×1000=20000辆/日。

与此同时，还可以找到最小割集如图7-30中的虚线所示。与之对应的最小割量为（9+6+5）×1000=20000辆/日。

由上述可见，用标号法找增广链以寻求最大流，不仅能求得从发点到收点的最大流，而且同时可以找到最小割集。最小割集是影响网络流量的咽喉，在这里弧的容量最小，因此它决定了整个网络的最大通行能力，若要提高网络的通行能力，必须从改造这个咽喉部位入手。