这个问题是我国学者管梅谷在1962年首先提出的，因此在国际上通称为中国邮路问题。

给定一个连通多重图G，若存在一条链过每边一次且仅一次，则称这条链为欧拉链。若存在一个简单圈过每边一次且仅一次，称这个圈为欧拉圈。一个图若有欧拉圈，则称为欧拉图。

【定理7.2】 连通多重图G有欧拉圈，当且仅当G中无奇点。

也就是说，如果在某邮递员所负责的范围内，街道图中没有奇点，那么他就可以从邮局出发，走过每条街道一次且仅一次，这样他走过的路程也是最短路程。

中国邮路问题变为在一个具有奇点的图中，如何将奇点连起来变为偶点成为欧拉图，使各边长之和最短。

【例7.10】 求解图7-28a的中国邮路问题。

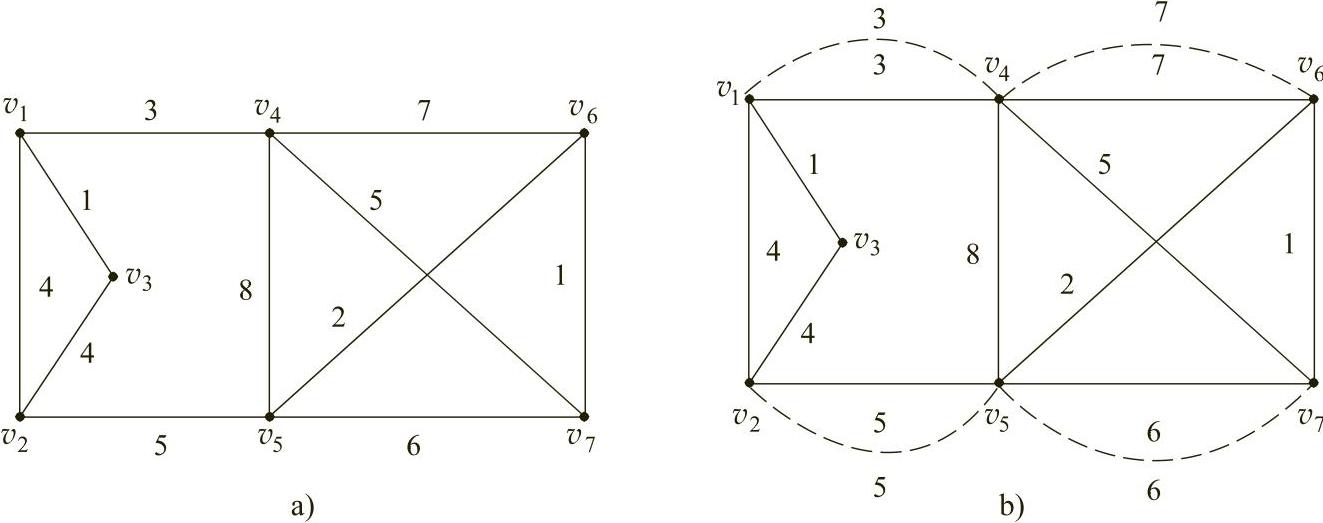
图7-28

解 1）虚拟边将所有奇点变为偶点，如图7-28b所示。虚拟边就是邮递员重复经过的街道。(www.daowen.com)

2）调整虚拟边。初始欧拉回路不一定是最短路。判断最短回路的准则是：①每条边最多重复一次，即相邻两点间最多虚拟一条边；②所有回路中虚拟边长之和不超过回路边长之和的一半。

在图7-28b中，回路H₁={v₄，v₅，v₇，v₆，v₄}的边长d（H₁）=8+6+1+7=22，其中虚拟边长为13，超过d（H₁）的一半，将虚拟边（v₄，v₆）和（v₅，v₇）去掉，在v₆与v₇之间加一条虚拟边。这时v₄和v₅变成了奇点，将虚拟边（v₁，v₄）和（v₂，v₅）改为虚拟边（v₁，v3）和（v₂，v₃），如图7-29a所示。

3）检查图7-29a，回路H₂={v₁，v₂，v₃，v₁}的边长d（H₂）=4+4+1=9，，虚拟边长为5，需要调整，将虚拟边（v₁，v₃）和（v₂，v₃）去掉，在（v₁，v₂）之间添加虚拟边

（v₁，v₂），如图7-29b所示。

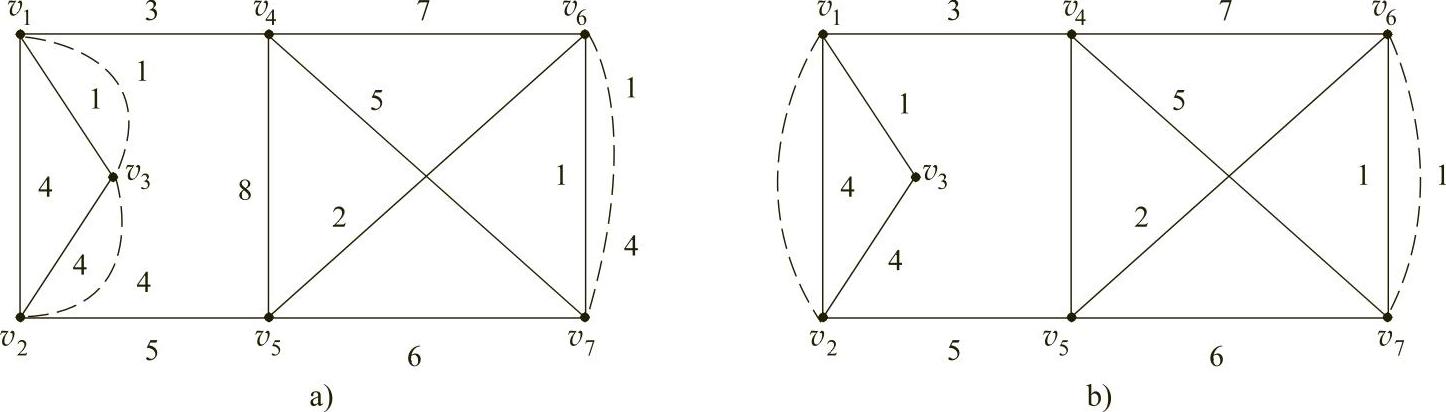
图7-29

4）继续检查，所有回路满足最短回路的准则，图7-29b是最短的欧拉回路，其中边（v₁，v₂）和（v₆，v₇）各重复一次。