一个推销商从n个城市v₁，v₂，…，v_n中某一个城市如v₁出发，到其他n-1个城市推销产品，每个城市都必须访问到并且只访问一次最后回到v₁，如何安排他的旅行路线使总距离最短，就是旅行售货员问题或货郎担问题。

旅行售货员问题虽然能用整数规划、动态规划等方法求解，但是当n较大时求解就不一定有效。一种可行的方法是求最小的Hamilton回路。下面介绍一下Hamilton回路。

设图G=[V，E]，若一个回路H过每个点一次且仅一次，则称H是G的一个Hamil-ton回路。与点v_i相关联的边数称为点的次（degree），记为d（v_i），次为奇数的点称为奇点，次为偶数的点称为偶点。若G中任意两个点v_i、v_j满足d（v_i）+d（v_j）≥n（n为图G的点数并且n≥3），则G中存在Hamilton回路。

旅行售货员所走的路线就是一个由n个城市构成的交通图G的一个Hamilton回路，旅行售货员问题就是寻找一个总距离最小的Hamilton回路。下面用例题介绍一种求满意解（不一定最优）的修正方法。

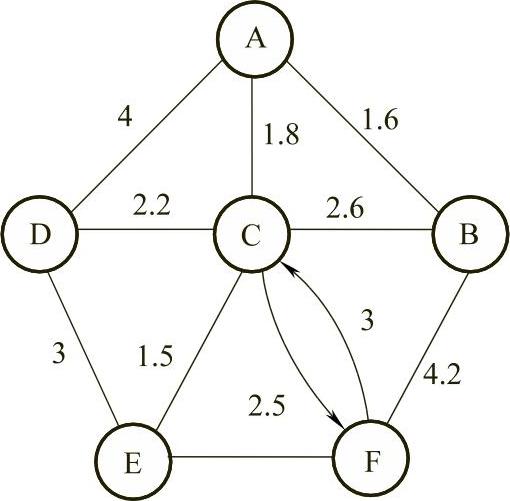
图7-27

【例7.9】 某电动汽车公司与学校合作，拟定在校园内开通无污染无噪声的“绿色交通”路线。图7-27是某大学教学楼和学生宿舍楼的分布图，其中C、F之间是两条单向通道，边上的数字为汽车通过两点间的正常时间（min）。电动汽车公司如何设计一条路线，使汽车通过每一处教学楼和宿舍楼一次后总时间最少。

解 1）显然图7-27存在Hamilton回路，将图表示成距离矩阵C，顺序为A，B，…，F，两点间没有边连接的时间为∞。

2）类似解指派问题（匈牙利算法）的第一步，每行每列分别减去该行该列最小元素，得到矩阵C₁，C₁与C的解相同。

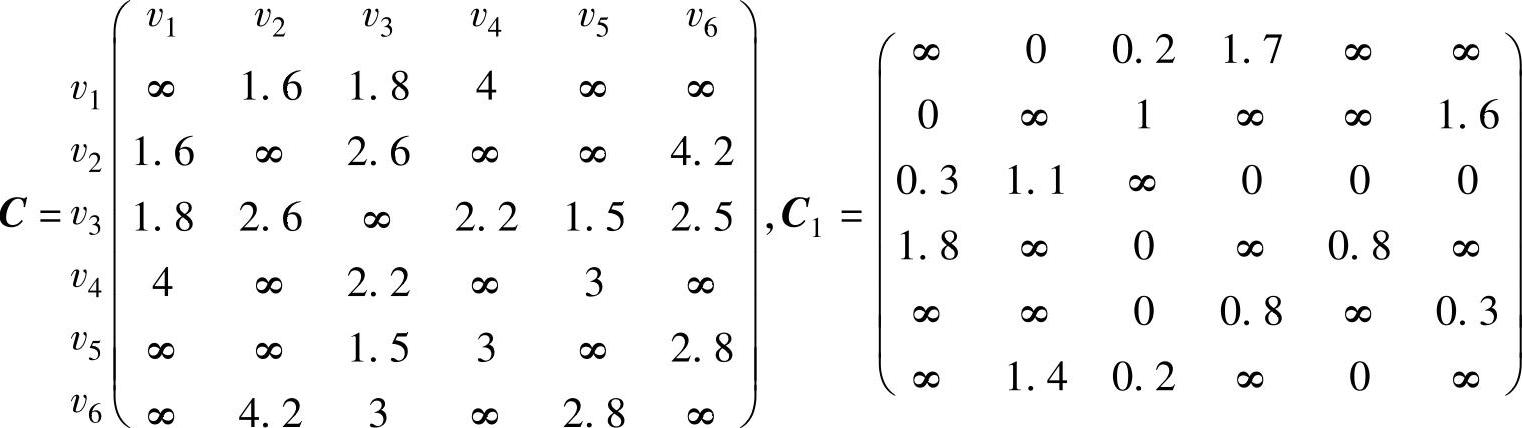
3）采用最近城市法（nearest neighbor heuristic），在C₁中取一个初始Hamilton回路H₁，起步可以从任意点开始，不妨从v₁出发，下一步到离v₁最近的点v₂，依次取v₃，v₆，v₅，v₄，v₁，回路H₁={v₁，v₂，v₃，v₆，v₅，v₄，v₁}的距离为：

C（H₁）=1.6+2.6+2.5+2.8+3+4=16.5(www.daowen.com)

4）修正回路H₁。在矩阵C₁中从v₁到v₂的距离c₁₂=0最短，去掉C₁的第一行第二列，为避免出现子回路v₁→v₂→v₁，令c₂₁=∞得到矩阵C₂。在C₂中第一行减去最小元素1，第一列减去最小元素0.3得到矩阵C₃。

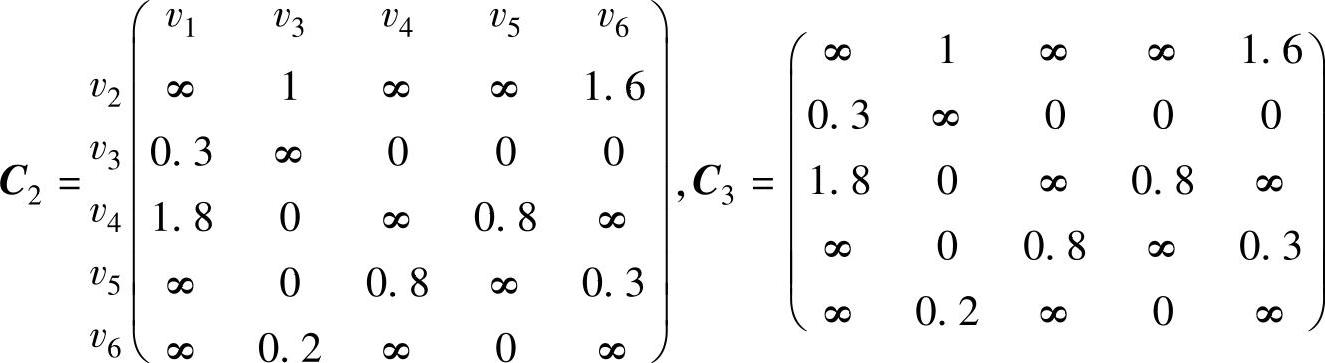
在C₃中，按最近城市法v₂下一步应达到v₃，从C₃看出最后一个点不能是v₅和v₆，下一步v₃不能选v₄只能选v₅和v₆，如果依次选v₅、v₆、v₄、v₁不能构成Hamilton回路，如果依次选v₆、v₅、v₄、v₁则回路与H₁相同，没有改进。

因此在C₃中，v₂下一步应达到v₆，取回路H₂={v₁，v₂，v₆，v₅，v₃，v₄，v₁}，距离为：

C（H₂）=1.6+4.2+2.8+1.5+2.2+4=16.3

5）与第4）步一样，去掉C₃中第一行和第五列，并且令c₆₁=∞（C₃中已是∞），得到矩阵C₄。矩阵C₄中每行每列都有零，在C₄中找一个与H₁、H₂不同的Hamilton回路，有两条不同的回路{v₁，v₂，v₆，v₅，v₄，v₃，v₁}和{v₁，v₂，v₆，v₃，v₅，v₄，v₁}，取第一条回路H₃={v₁，v₂，v₆，v₅，v₄，v₃，v₁}，即v₆下一步达到v₅，距离为：

C（H₃）=1.6+4.2+2.8+3+2.2+1.8=15.6

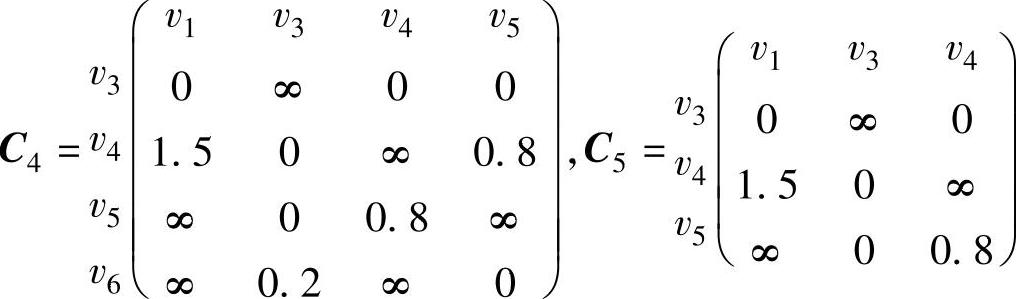
去掉C₄中第四行第四列，得到矩阵C₅。C₅中不存在H₁、H₂、H₃不同的回路，H₃为最小的Hamilton回路。

电动汽车公司的行车路线是A→B→F→E→D→C→A，汽车在校园行驶一圈需要15.6min。

从例题的计算看出，最后结果很大程度上依赖于前面走过的路线，如第一步从某个点出发到另一个点确定后，就不能再变动，其结果可能不是最小Hamilton回路。在例7.14中，由矩阵C₁第一步从v₂开始到v₁取一个Hamilton回路，最后结果就与例题结果不同。开始可以取不同的Hamilton回路，重复计算几次，从中筛选较优的结果。