前节讨论网络最大流时，只描述了流量的大小问题，而未考虑网络流的费用问题。在实际工程中，涉及“流”的问题时，人们考虑的不只是流量，而且还有费用的因素。因此，在一个网络流中求出一条可行流后，满足流量达到一个固定数使总费用最小，就是工程中的最小费用流问题。另一个问题是满足流量达到最大使总费用最小，称为最小费用最大流问题。

与最大流的标号算法相比，最小费用流的标号算法不仅要找增广链，更重要的是寻找所有增广链中费用最小的那条增广链。针对这个问题，首先考虑一下，当沿着一条关于可行流f的增广链u，以Δ=1调整f，得到新的可行流f′时，费用b（f′）比b（f）增加的量为：

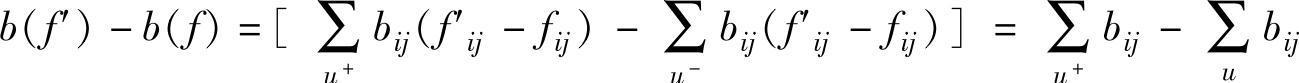
我们把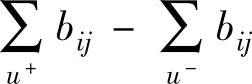称为这条增广链u的“费用”。

可以证明，流量为v^（k-1）的可行流f^（k-1），其最小费用增广链的调整量为θ，则调整后的可行流f（k）是流量v（k）=v^（k-1）+θ的最小费用流。

最小费用流算法的基本思路是：给定一个初始流量v^（0），找出其最小费用流f^（0），如初始流量为零的流量f^（0）={0}是最小费用流。然后利用Ford-Fulkerson标号算法寻找一条从发点到收点的最小费用增广链，调整量为θ，调整后的流量为v（0）+θ。不断寻找最小费用增广链和调整流量，直到流量等于事先给定的流量v为止。

设给定的流量为v，则求网络最小费用最大流的算法可归纳如下：

第一步，取初始流量为零的可行流f（0）={0}。

第二步，令网络图中所有弧的权等于d_ij，得到一个赋权图D，用Dijkstra算法求出最短路，这条最短路就是初始最小费用增广链u。

第三步，调整流量。前向弧上令θ=c_ij-f_ij，后向弧上令θ=f_ij，调整量为θ=min（θ_j）。调整后得到的最小费用流f（k），流量为v（k）=v（k^-1）+θ，当v（k）=v时计算结束，否则转到第四步。

第四步，作赋权图D并寻找最小费用增广链。

1）最小费用流f（k^-1）的流量为v（k^-1）＜V时，将网络的费用转化为权w_ij，其含义等价于最短路中的距离。对可行流f（k^-1）的最小费用增广链上的弧（i，j）作如下变动：

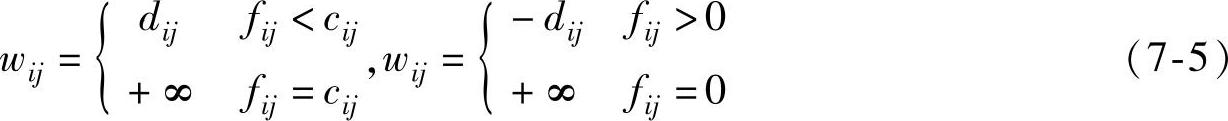
式（7-5）的使用方法如下：

第一种情形，当弧（i，j）上的流量满足0<f_ij＜c_ij时，在点v_i与v_j之间添加一条方向相反的弧（j，i），权为（-d_ij）。

第二种情形，当弧（i，j）上的流量满足f_ij=c_ij时将弧（i，j）反向变为（j，i），权为（-d_ij）。不在最小费用增广链上的弧不作任何变动，得到一个赋权网络图D。

2）求赋权图D从发点到收点的最短路，如果最短路存在，则这条最短路就是f（k^-1）的最小费用增广链，转第二步。

赋权图D的所有权非负时，可用Dijkstra算法求最短路，存在负权时用Floyd算法。

3）如果赋权图D不存在从发点到收点的最短路，说明v（k^-1）已是最大流量，不存在流量等于v的流，计算结束。

【例7.8】 图7-24是一个运输网络图，弧上的数字为（c_ij，b_ij），c_ij表示总运量，b_ij为相应的运输费用，现试制定一个通行能力v=15及最小费用最大流的运输方案。

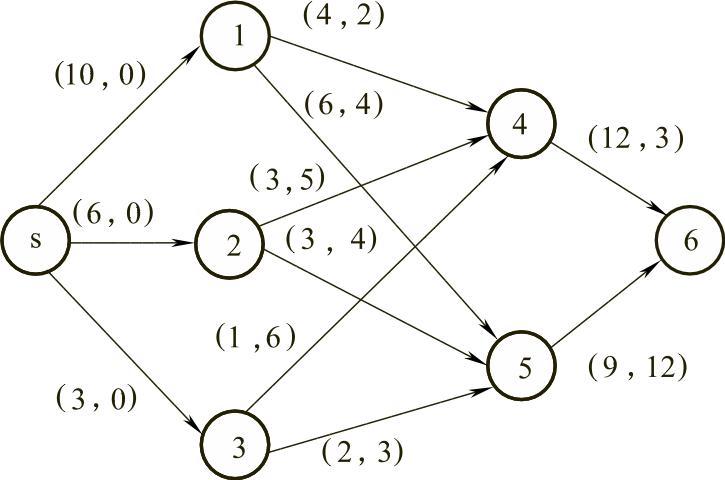
图7-24

解 1）令所有弧的流量等于零，得到初始可行流f^（0）={0}，流量v^（0）=0，总运费d（f^（0））=0。

2）弧的权数等于费用b_ij，用Floyd算法求出该赋权图的最短路。最小费用增广链u₁：Ⓢ→①→④→⑥，见图7-25a。(www.daowen.com)

3）调整流量。调整量θ=4，对f（0）={0}进行调整得到f^（1），见图7-25b，括号内的数字为弧的流量，网络流量v^（1）=4，总运费：

d（f^（1））=0×4+2×4+3×4=20

4）v^（1）=4＜15，没有得到最小费用流。在图7-25b中，弧（s，1）和（4，6）满足条件0＜f_ij<c_ij，添加两条边（1，s）和（6，4），权分别为“0”和“-3”，边（1，s）可以去掉；弧（1，4）上有f_ij=c_ij说明已饱和，将弧（1，4）反向变为（4，1），权为“-2”，见图7-25c。

5）继续转到步骤二，求出最小费用增广链u₂：Ⓢ→②→④→⑥，调整量θ=3，调整后得到的最小费用流f^（2），流量v^（1）=4，见图7-25d，总运费：

d（f^（2））=2×4+3×7+5×3=44

6）v（2）=7＜15，需要对最小费用增广链u₂上的弧进行调整。图7-25c中，弧（s，2）和（4，6）满足条件0<f_ij＜c_ij，添加两条边（2，s）和（6，4），权分别为“0”和“-3”，边（1，s）可以去掉；弧（6，4）已经存在，弧（2，4）上f_ij=c_ij说明已饱和，将弧（2，4）反向变为（4，2），权为“-5”，见图7-25e。

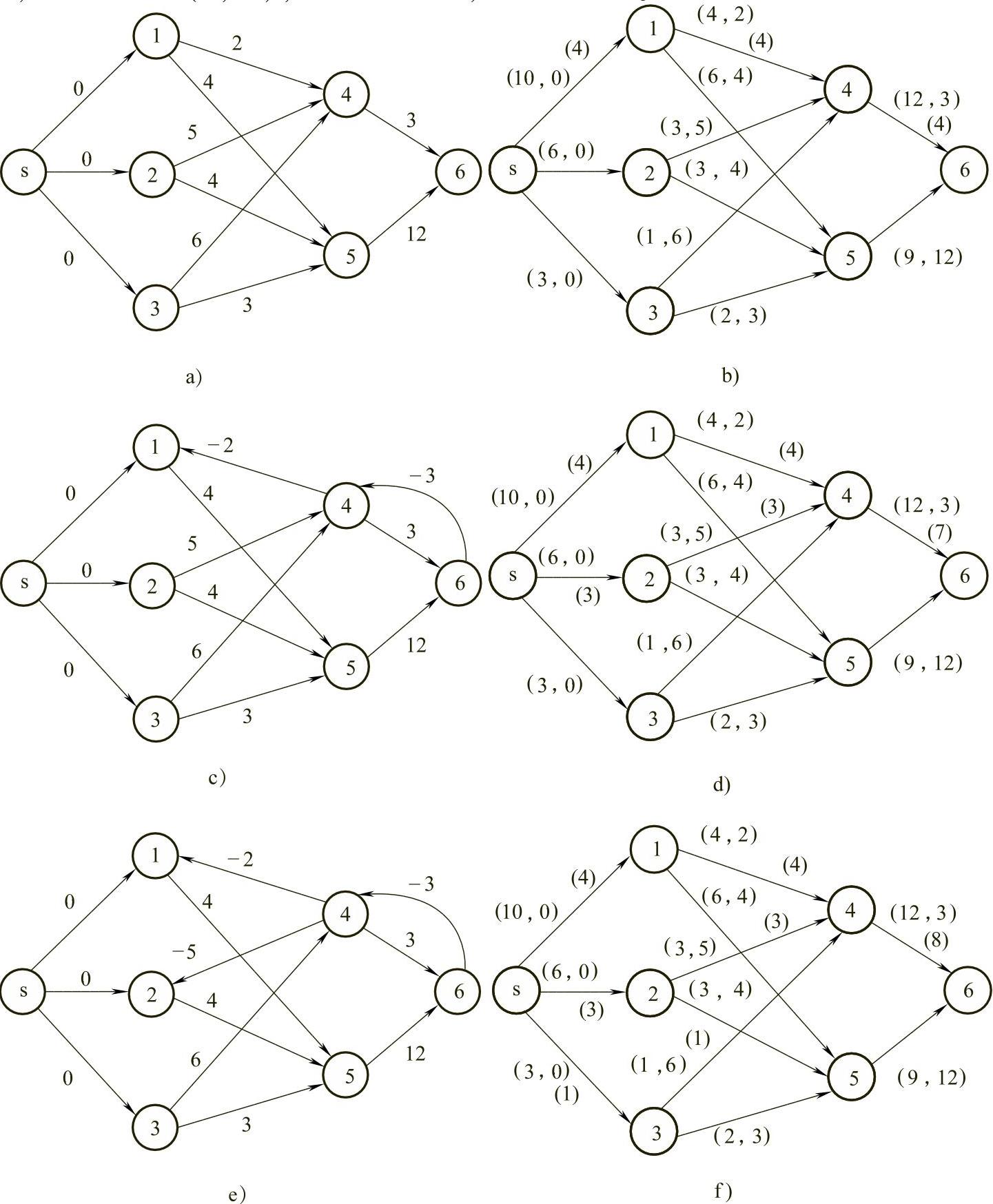
图7-25

a）f^（0），赋权图D₀ b）f^（1） c）f^（1），赋权图D₁ d）f^（2） e）f^（2），赋权图D₂ f）f^（3）

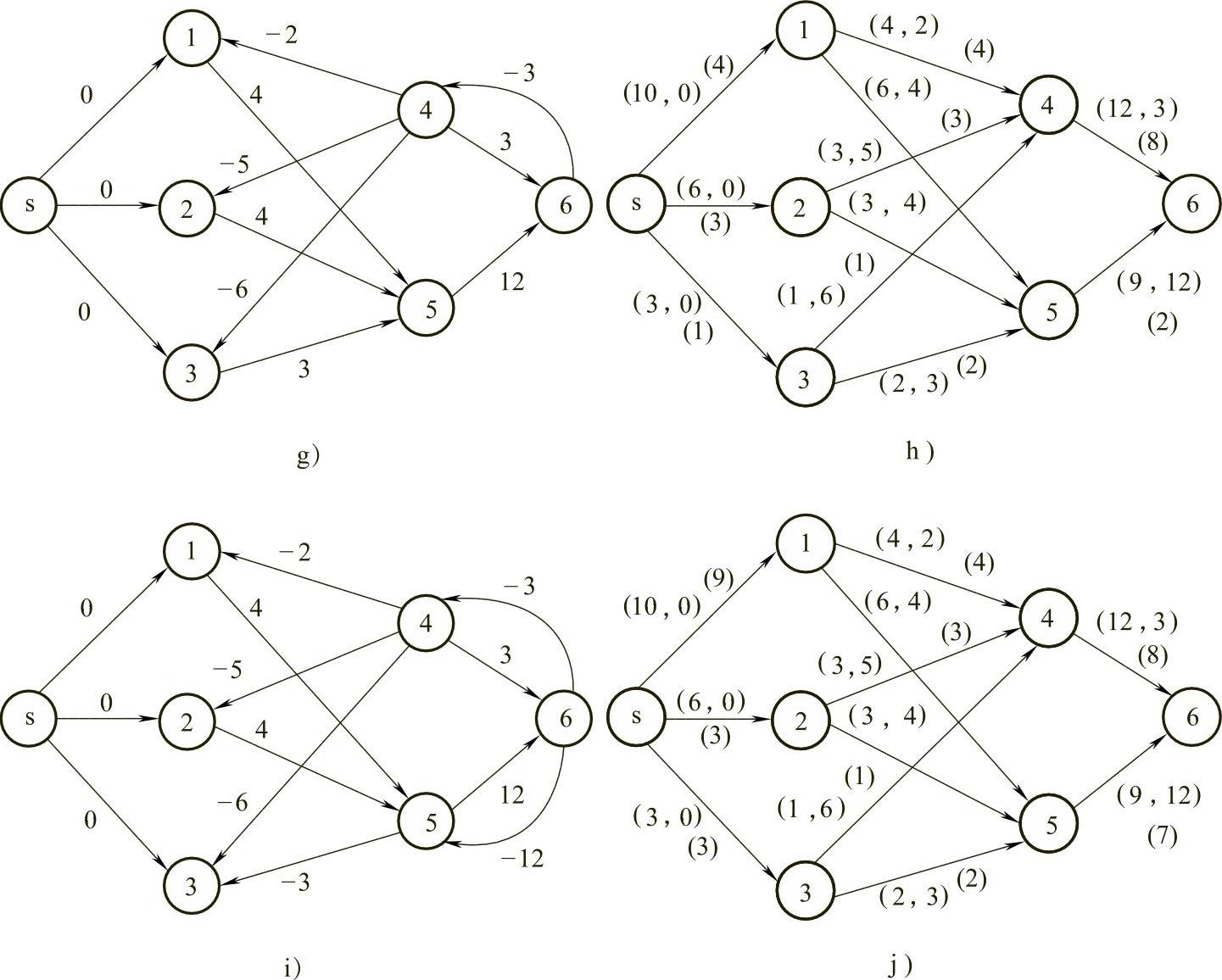
图7-25 （续）

g）f^（3），赋权图D₃ h）f^（4） i）f^（4），赋权图D₄ j）f^（5）

7）继续重复步骤2）、3）及4），得到图7-25i，最小费用增广链u₅：Ⓢ→①→⑤→⑥，调整量θ=6，取θ=5，流量v^（5）=v=15得到满足，最小费用流见图7-25j，问题1计算结束。

8）求最小费用最大流。对图7-25i的最小费用增广链u₅，取调整量θ=6对流量调整，得到图7-26a及赋权图7-26b。

9）图7-26b的最小费用增广链u₆：Ⓢ→②→⑤→⑥，调整量θ=1，流量v（6）=17，最小费用流为f^（6）及赋权图，见图7-26c、d。图7-26d不存在从v_s发点到v₆的最短路，则图7-26c的流量就是最小费用最大流，最大流量v=17，最小的总运费为：

d（f）=2×4+4×6+5×3+4×1+6×1+3×2+3×8+12×9=195

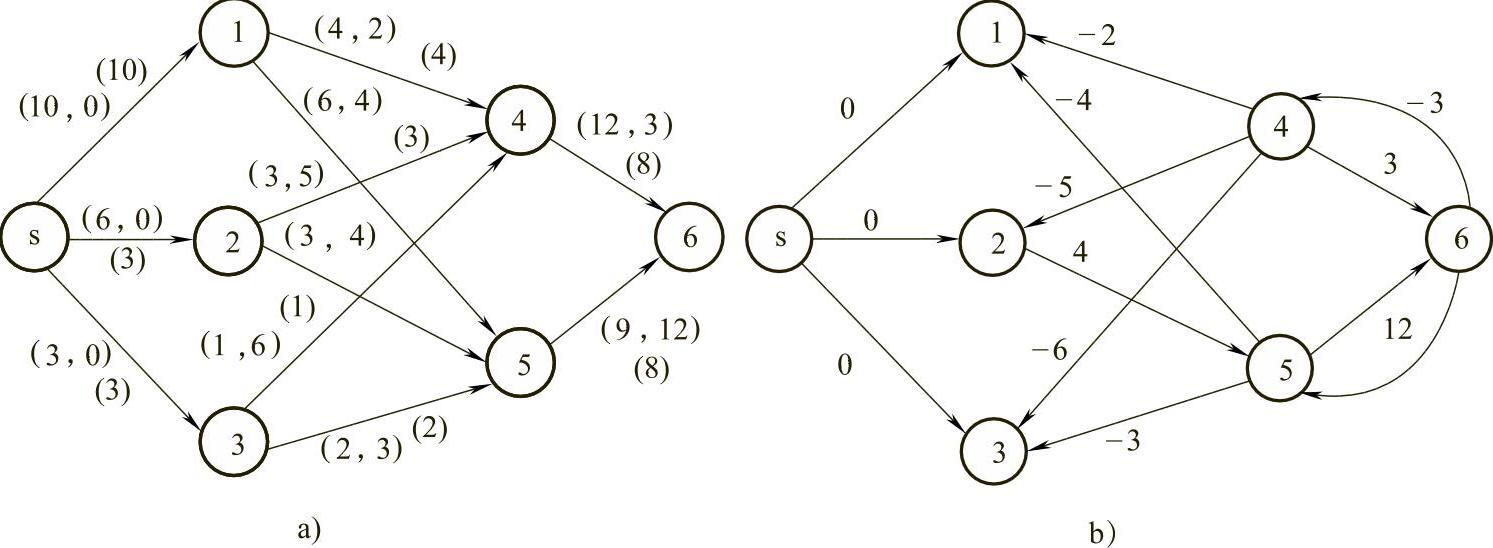
图7-26

a）f^（5） b）f^（5），赋权图D₅

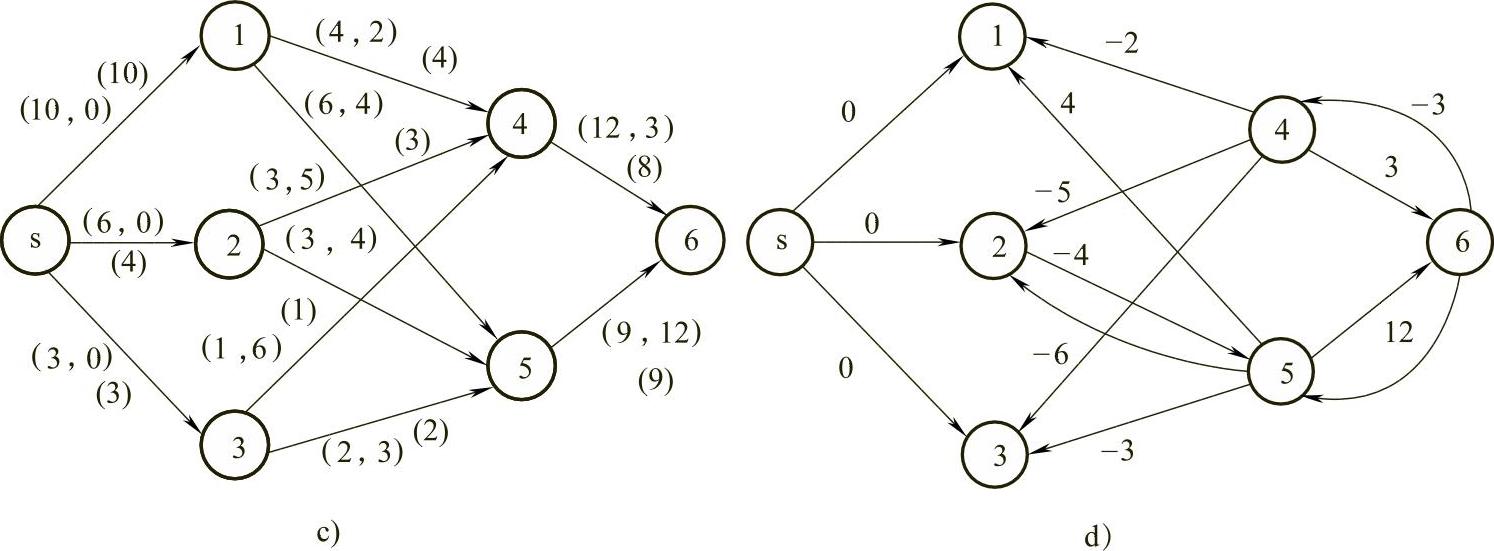
图7-26 （续）

c）f^（6） d）f^（6），赋权图D₆