寻找最大流的算法是从某个可行流f开始，用标号法求关于可行流f的增广链。若增广链存在，则可以经过调整，得到新的可行流f′，其流量val（f′）大于val（f），然后再寻找f′的增广链，再调整，依次进行下去直到增广链不存在为止，因此可得到定理7.1。

【定理7.1】 可行流f是最大流的充分必要条件是不存在发点到收点的增广链。

Ford-Fulkerson标号算法的步骤如下：

第一步，找出第一个可行流，例如所有弧的流量f_ij=0。

第二步，对点进行标号找一条增广链。

1）发点标号（∞）。

2）选一个点v_i已标号并且另一端未标号的弧沿着某条链向收点检查。

①如果弧的方向向前（前向弧）并且有f_ij＜c_ij，则v_j标号θ_j=c_ij-f_ij。

②如果弧的方向指向v_i（后向弧）并且有f_ij>0，则v_j标号θ_j=f_ji。

当收点已得到标号时，说明已找到增广链，依据v_i的标号反向跟踪得到一条增广链。当收点不能得到标号时，说明不存在增广链，计算结束。

第三步，调整流量。

1）求增广链上点v_i的标号的最小值，得到调整量。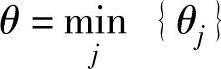

2）调整流量。

得到新的可行流f₁，去掉所有标号，返回到第二步从发点重新标号寻找增广链，直到收点不能标号为止。

【例7.7】 求图7-15发点v₁到收点v₇的最大流及最大流量。

解 1）给出一个初始可行流，弧的流量放在括号内，如图7-16所示。

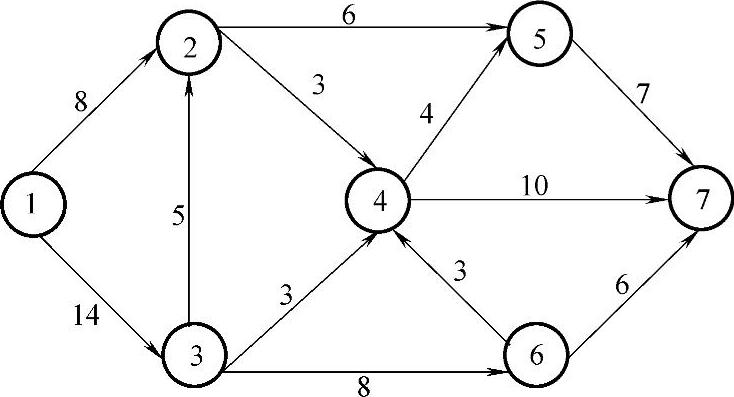
图7-15

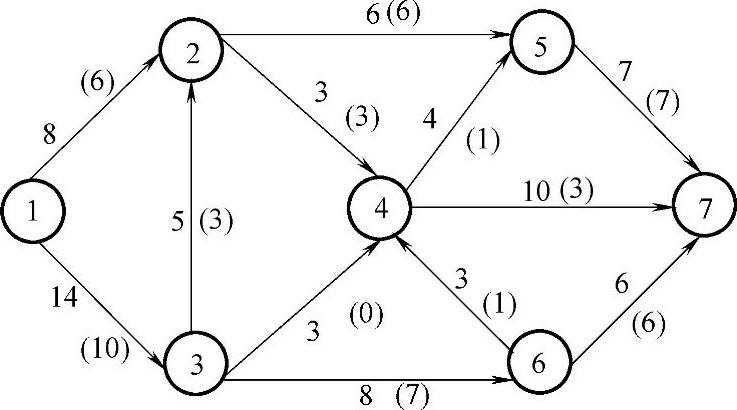
图7-16

2）标号寻找增广链。发点标号∞，用“□”表示标在发点v₁处。v₁已标号，与v₁相邻的两个点v₂和v₃都没有标号，任意选一个点检查，如选v₂。v₂能否得到标号要看是否满足上述步骤二的条件①或②中的一个。弧（1，2）的箭头指向v₂是前向弧，因为f₁₂=6＜c₁₂=8满足条件①，因此v₂可以标号，给v₂标号θ₂=c₁₂-f₁₂=8-6=2，见图7-17a。

选择已标号点v₂，与v₂相邻并且没有标号的点有v₃、v₄和v₅，逐个检查能否标号，如果某个点能标号就一直向前，不必要相邻点都标号，如果点不能标号再检查下一个点。弧（2，4）和（2，5）是向前弧，流量等于容量不满足条件①，v₄和v₅不能标号。再检查v₃，弧（3，2）是后向弧，有f₃₂=3＞0，满足条件②，给v₃标号θ₃=f₃₂=3。

选择已标号点v₃，由条件①，v₄和v₆都能标号，选择v₄标号θ₄=c₃₄-f₃₄=3，接下来给v₇标号θ₇=c₄₇-f₄₇=10-3=7，见图7-17b。

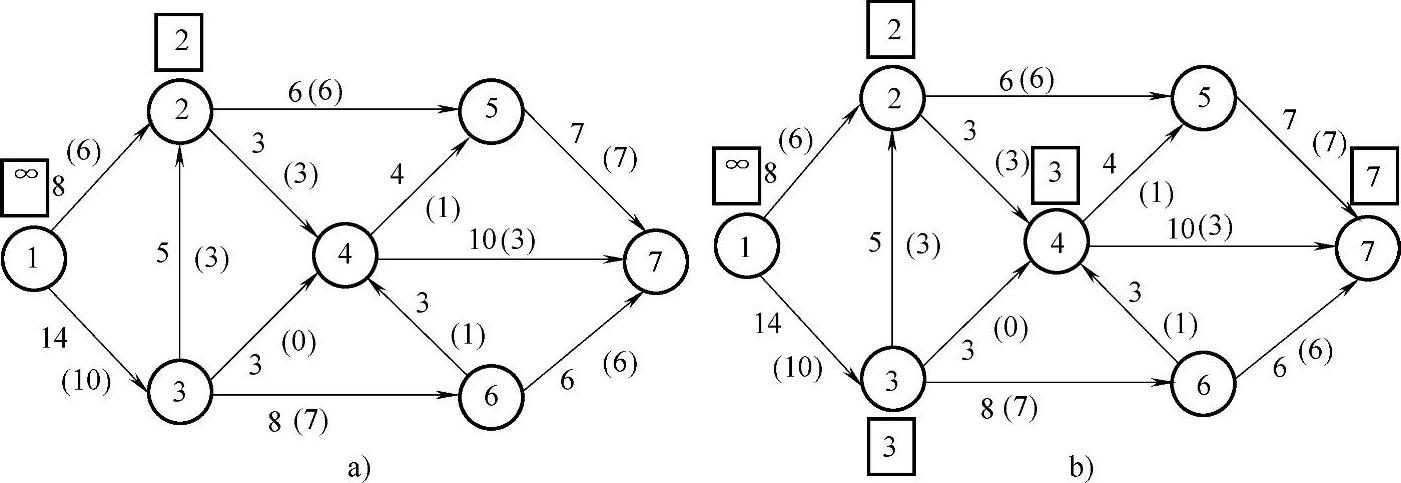
图7-17(www.daowen.com)

v₇已标号说明找到一条增广链，沿着标号的路线追踪得到增广链u={（1，2），（3，2），（3，4），（4，7）}，u⁺={（1，2），（3，4），（4，7）}，u^-={（3，2）}，调整量为增广链上点标号的最小值：

θ=min{∞，2，3，3，7}=2

3）调整增广链上的流量。在图7-16中，弧（1，2）、（3，4）及（4，7）上的流量分别加上2，弧（3，2）上的流量减去2，其余弧上的流量不变，得到图7-18。

4）对图7-18标号。发点标号∞，v₂不能标号，v₃标号θ₃=c₁₃-f₁₃=4。v₂、v₄和v₆都可以标号，当选择v₂标号θ₂=c₃₂-f₃₂=4时，v₄和v₅不能标号，不能说明不存在增广链，这时应回头选择v₄和v₆标号。这里选择v₄标号θ₄=c₃₄-f₃₄=1，继续标号，选择v₇标号θ7=c47-f47=5。得到发点到收点的增广链u=u⁺={（1，3），（3，4），（4，7）}，见图7-19。调整量为：

θ=min{∞，4，1，5}=1

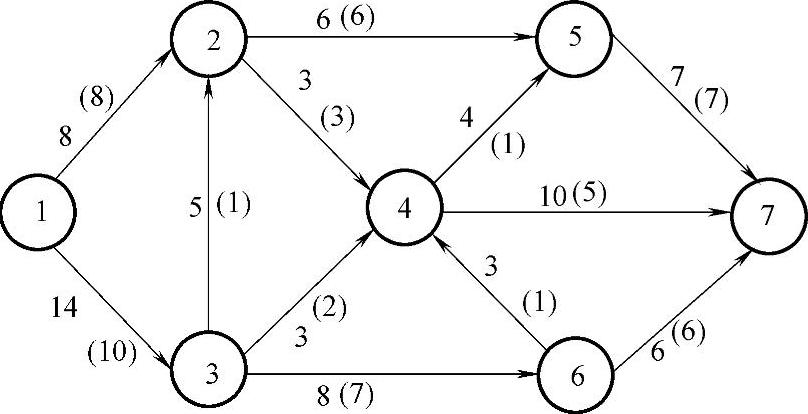
图7-18

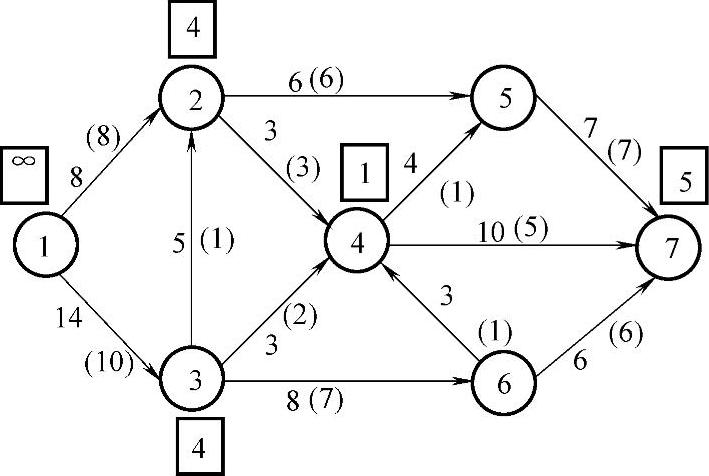
图7-19

对图7-18的流量进行调整，增广链上弧的流量加上1，其余弧的流量不变，得到图7-20。

5）对图7-20标号，得到一条增广链u={（1，3），（3，6），（6，4），（4，7）}，见图7-21。调整量为：

θ=min{∞，3，1，2，4}=1

对图7-20的流量进行调整，增广链上弧的流量加上1，其余弧的流量不变，得到图7-22。

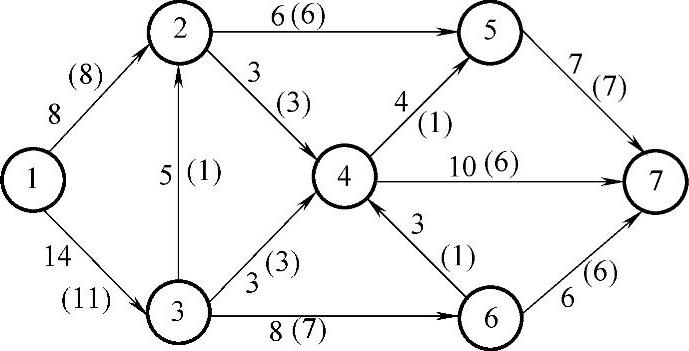
图7-20

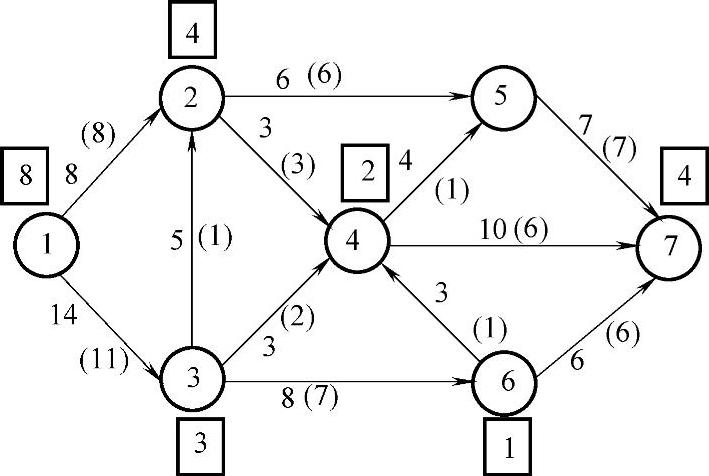
图7-21

6）对图7-22标号。v₁、v₃和v₂得到标号，其余点都不能标号，说明已不存在发点到收点的增广链，见图7-23。由定理7.1知图7-22所示的流是最大流，网络的最大流量为：

v=f₁₂+f₁₃=8+12=20

标号法计算完成。

对于无向图最大流的计算，将所有弧都理解为是前向弧，对一端v_i已标号另一端v_j未标号的边只要满足c_ij-f_ij>0则v_j就可标号（c_ij-f_ij），调整流量的方法与有向图计算相同。

图7-22

图7-23