1.网络与流

图7-13所示的网络图中定义了一个发点v₁，称为源（source，supply node），定义了一个收点v₇，称为汇（sink，demand node），其余点v₂，v₃，…，v₆为中间点，称为转运点（transshipment node）。如果有多个发点和收点，则虚设发点和收点转化成一个发点和收点。图中的权是该弧在单位时间内的最大通过能力，称为弧的容量（capacity）。

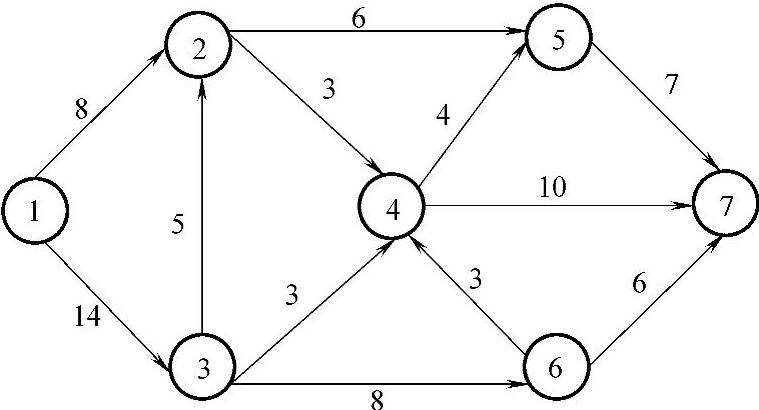
图7-13

设c_ij为弧（i，j）的容量，f_ij为弧（i，j）的流量。容量是弧（i，j）单位时间内的最大通过能力，流量是弧（i，j）单位时间内的实际通过量，流量的集合f={f_ij}称为网络的流。发点到收点的总流量记为v=val（f），v也是网络的流量。

2.可行流与最大流

由图7-13所示的实际交通网络图可知，对于流有两个明显的要求：一是每个弧上的流量不能超过它的容量；二是中间点的流量为0，这是因为中间点只起转运作用，流进该中间点的流量应该等于流出的流量。也即可行流应满足以下条件：

1）容量限制条件：对于每条弧都有0≤f_ij≤c_ij。

2）流量守恒条件：①对于所有中间点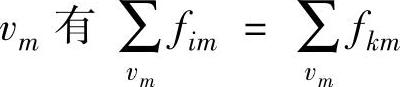。②发点v_s流出的总流量等于流入收点v_t的总流量，即。

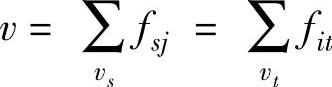如果存在有流入发点的流和收点流出的流，应从式中减去，条件②变为：

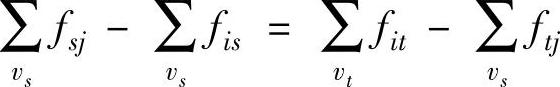
综上所述，网络最大流问题就是在满足上述条件的基础上寻找一个流f，使其流量达到最大。(www.daowen.com)

3.增广链

从发点到收点的一条路线（弧的方向不一定相同）称为链，从发点到收点的方向规定为链的方向。与链的方向相同的弧称为前向弧。与链的方向相反的弧称为后向弧。对于一个可行流f，使f_ij=c_ij的弧称之为饱和弧，f_ij＜c_ij的弧称之为非饱和弧。

设f是一条可行流，如果存在一条从发点v_s到收点v_t的链，满足：

1）所有前向弧u⁺上0≤f_ij＜c_ij。

2）所有后向弧u^-上0≤f_ij＜c_ij。

则该链称为增广链。

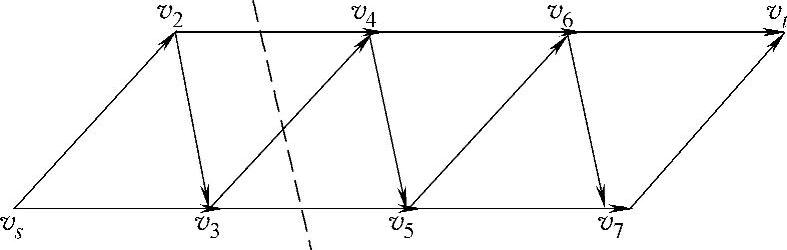
图7-14

4.割集与割量

割集是分割网络发点与收点的一组弧集合，从网络中去掉这组弧就断开网络，发点就不能到达收点。图7-14中，网络被切成两半，一半包含发点v_s，一半包含收点v_t，则弧集E₁={（v₂，v₄）（v₃，v₄），（v₃，v₅）}被称为割集。

一般情况下，将网络的点集V分割成两部分V₁及V₁，其中发点v_s∈V₁，收点v_t∈V₁，称箭尾在V₁中、箭头在V₁中弧的集合为分割网络发点与收点的割集，记为（V₁，V₁）。割集中弧的容量之和称为割量（割集的容量），记为C（V₁，V₁）。对点集V的不同分割得到不同的割量，割量最小的割集称为最小割集。