前面介绍了有正赋权图的有向图和无向图的最短路问题，对于求任意两点间的最短路、混合图的最短路以及有负权图的最短路，介绍一种新的计算方法——Floyd（弗洛伊德）算法。

Floyd算法基本步骤如下：

1）写出v_i一步到达v_j的距离矩阵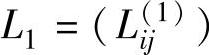，L₁也是一步到达的最短距离矩阵。如果v_i与v_j之间没有边关联，则令c_ij=+∞。

2）计算两步最短距离矩阵。设v_i到v_j经过一个中间点v_r两步到达v_j，则v_i到v_j的最短距离为：

最短距离矩阵记为。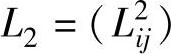

3）计算k步最短距离矩阵。设v_i经过中间点v_r到达v_j，v_i经过k-1步到达点v_r的最短距离为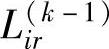，v_r经过k-1步到达点v_j的最短距离为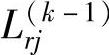，则v_i经过k步到达v_j的最短距离为：

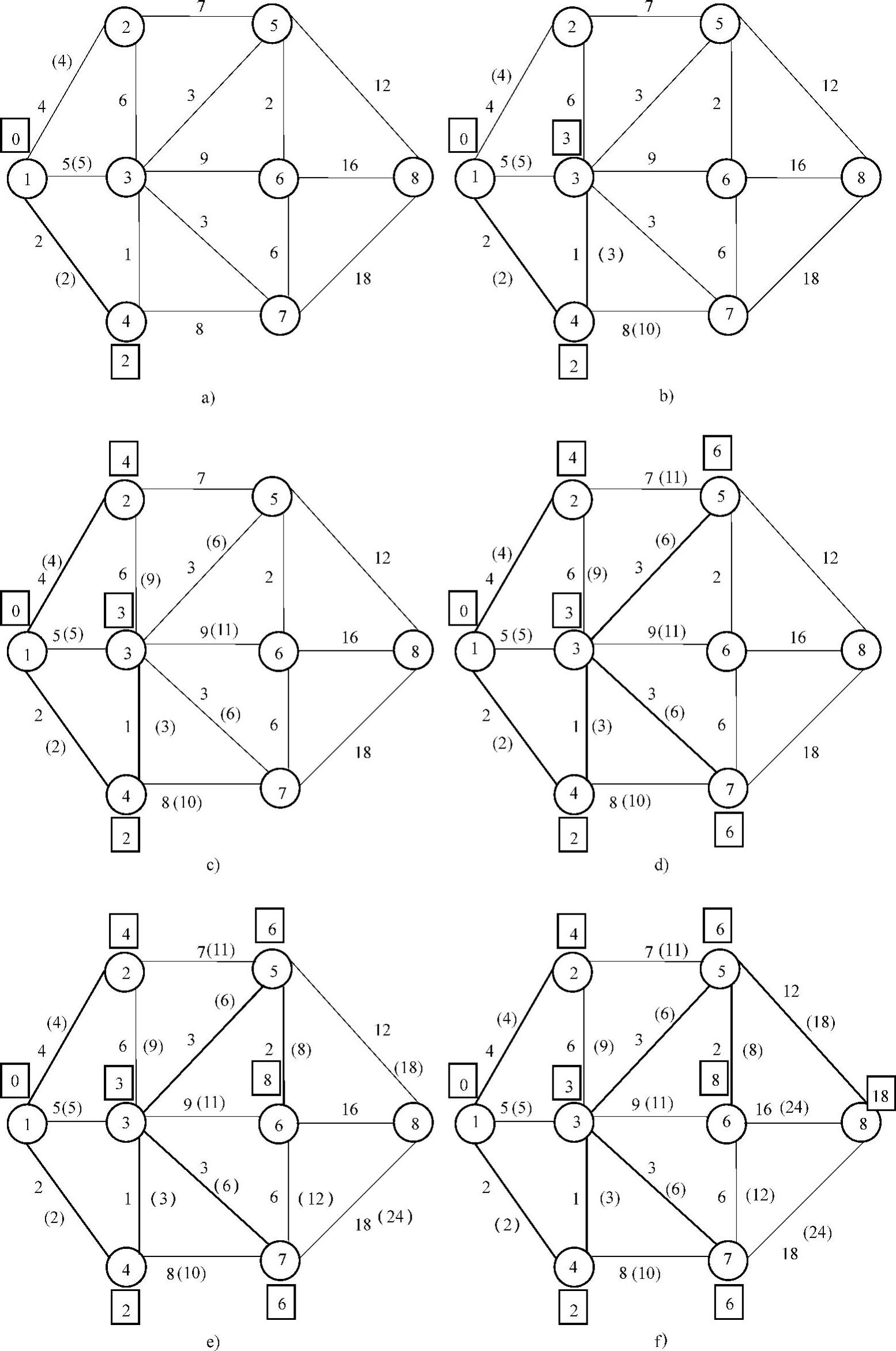
图7-10

最短距离矩阵记为。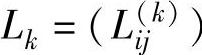

4）比较矩阵L_k与L_k-1，当L_k=L_k-1时得到任意两点间的最短距离矩阵L_k。

设图的点数为n并且c_ij≥0，迭代次数k由式（7-3）估计得到。

图7-11

应当注意，这里的k是迭代次数，不一定等于v_i到达v_j最短路中间所经过的点数，中间点最多等于2^k-1-1，经过一条边看成是一步，则最多走2^k-1步，区分公式中的“步”与实际经过的“步”之间的关系，就不难理解式（7-2）的含义。

【例7.5】 图7-11所示为一张8个城市的铁路交通图，铁路部门要制作一张两两城市间的距离表。这个问题实际就是求任意两点间的最短路问题。

解 1）依据图7-11，写出任意两点间一步到达距离表L₁，见表7-1。本例n=8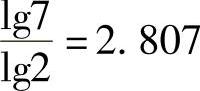，，因此计算到L₃。

2）由式（7-1）得到矩阵L₂，见表7-2。

表7-2计算示例。等于表7-1中第i行与第j列对应元素相加取最小值。例如，v₄经过两步（最多一个中间点）到达v₃的最短距离是：

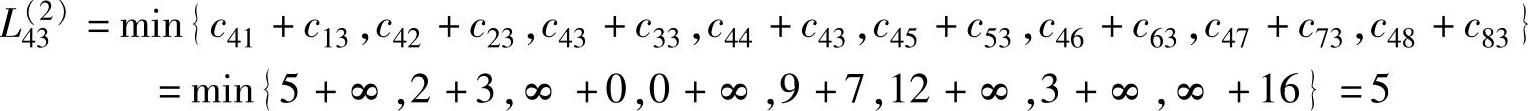
3）由式（7-2）得到矩阵L₃，见表7-3。

表7-3计算示例。等于表7-2中第i行与第j列对应元素相加取最小值。例如，v₃经过三步（最多3个中间点4条边）到达v₆的最短距离是：

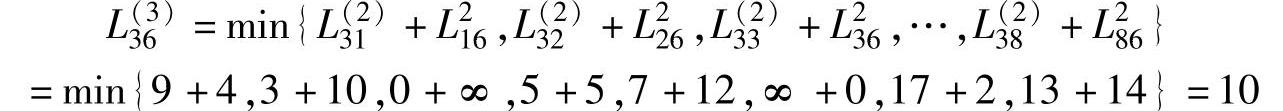(www.daowen.com)

由表7-2及表7-1可知，最短距离由4条边长之和构成：

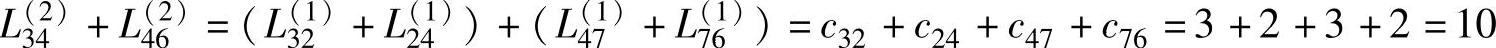
则v₃到v₆的最短路线是：v₃→v₂→v₄→v₇→v₆。

表7-3就是最优表，即任意两点间的最短距离。取表中下三角得到8个城市间的铁路交通距离表。

表7-1 最短距离表L₁

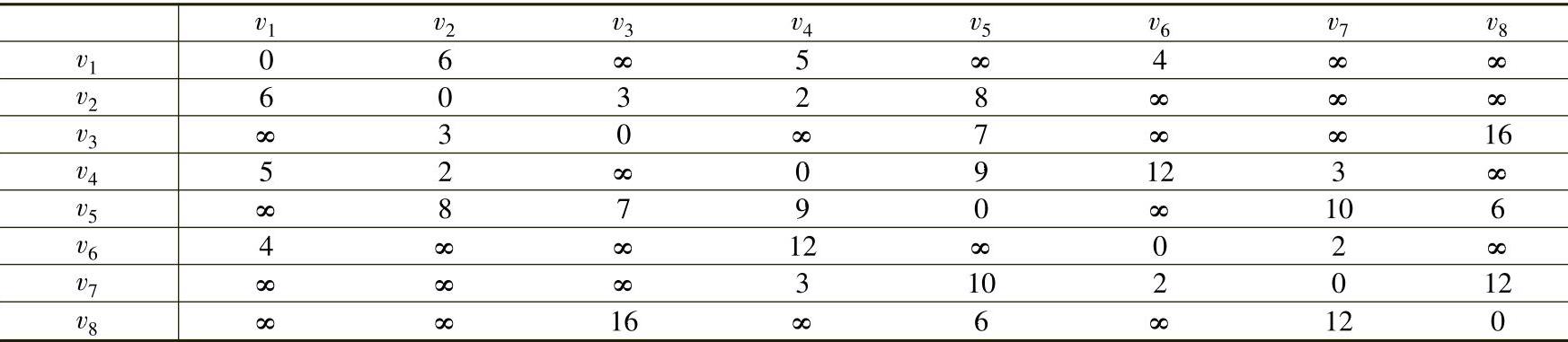
表7-2 最短距离表L₂

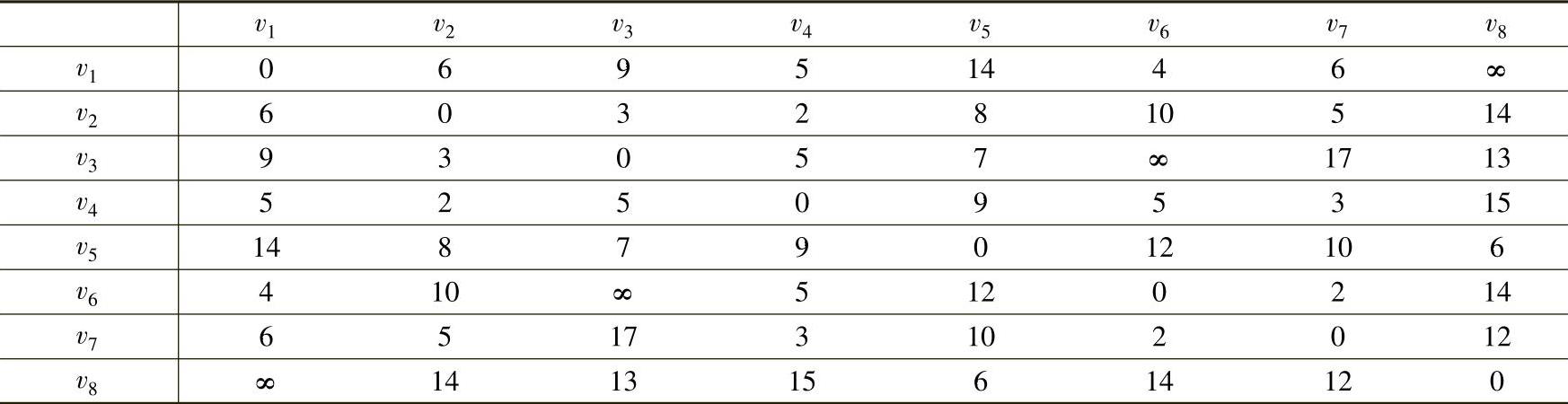
表7-3 最短距离表L₃

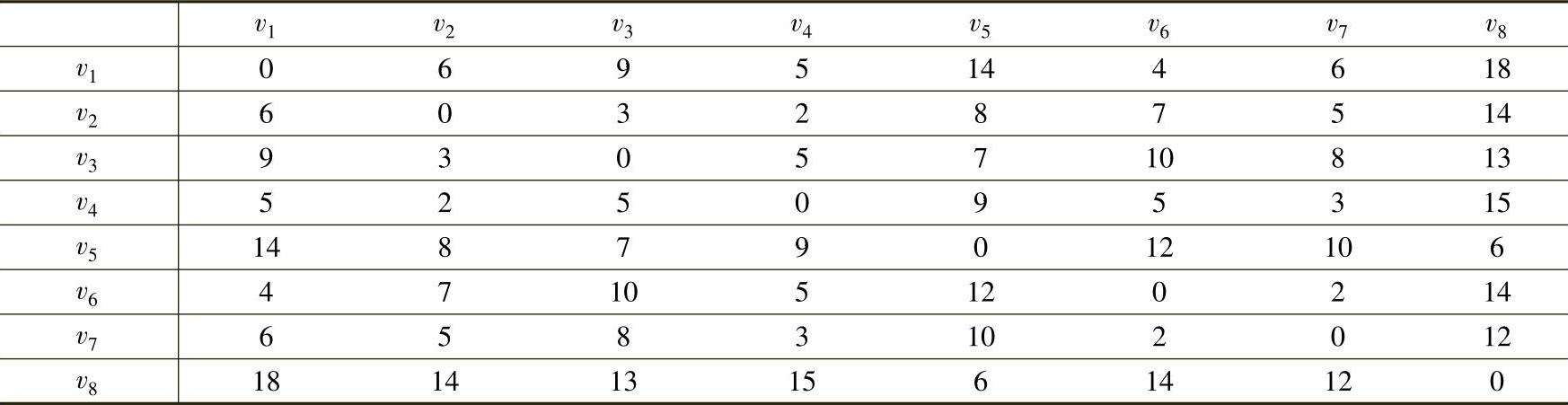
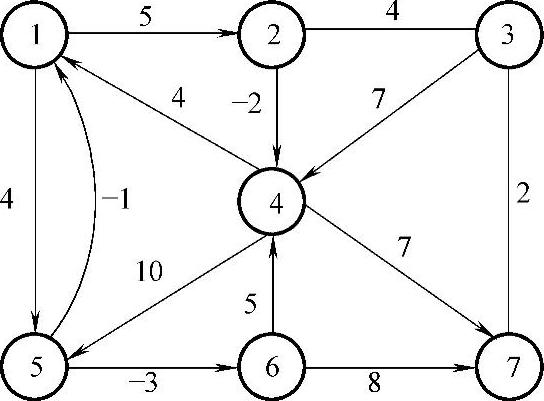
图7-12

【例7.6】 求图7-12中任意两点间的最短距离。

解 图7-12是一个混合图，有3条边的权是负数，有两条边无方向。依据图7-12，写出任意两点间一步到达距离表L₁。表中第一列的点表示弧的起点，第一行的点表示弧的终点，无方向的边表明可以互达，如表7-4所示。计算过程见表7-5～表7-7。

表7-4 一步到达距离表L₁

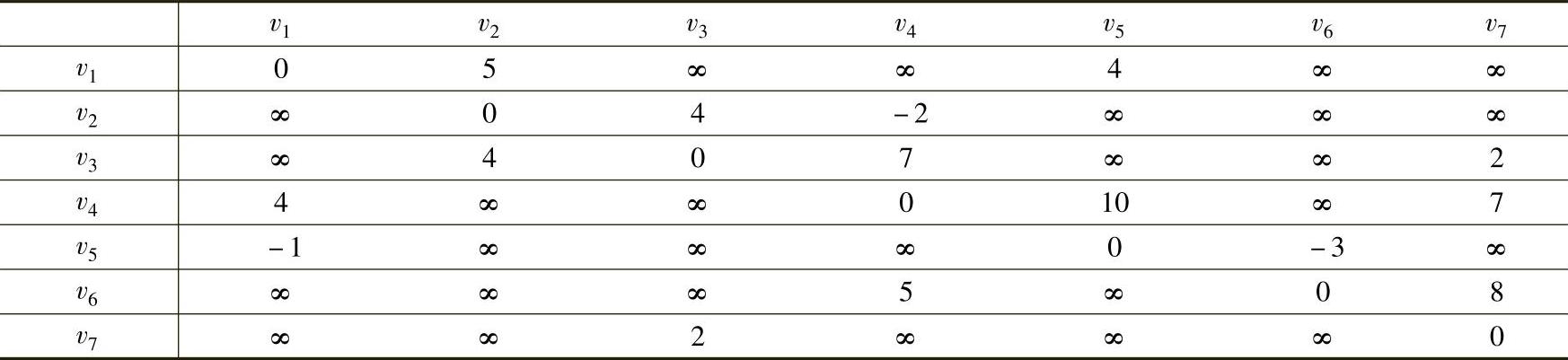
表7-5 一步到达距离表L₂

表7-6 一步到达距离表L₃

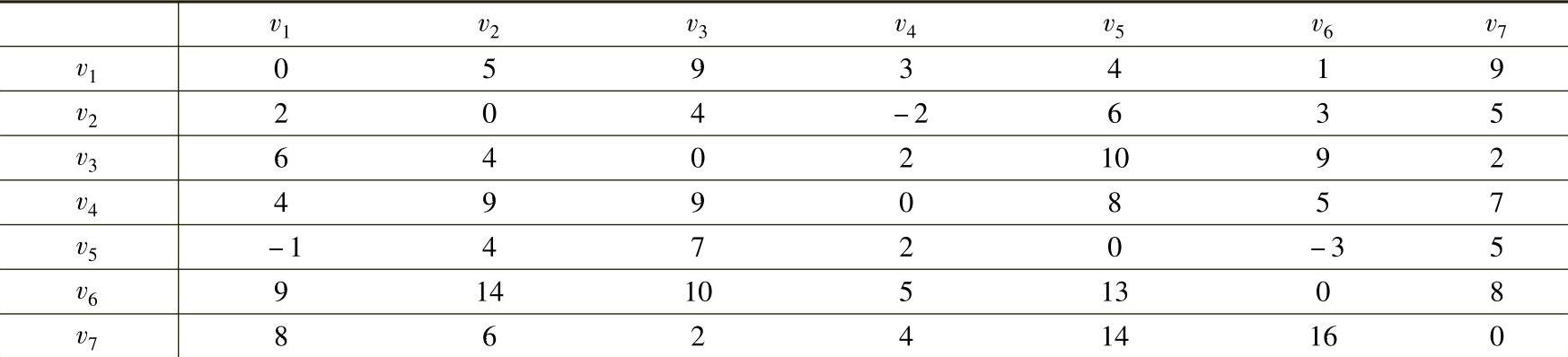
表7-7 一步到达距离表L₄

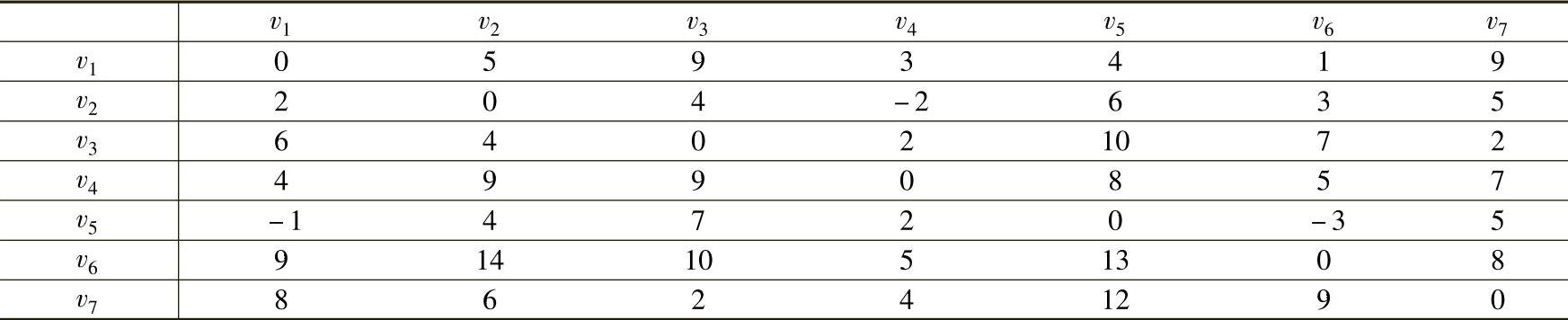
经计算L₄=L₅，L₄是最优表。表7-7不是对称表，v_i到v_j与v_j到v_i的最短距离不一定相等。对于有负权图情形，式（7-3）失效。