对于求解最短路问题，在图上计算更为简单。下面介绍求解有向图的一种算法——Di-jkstra（狄克斯屈拉）算法。

Dijkstra（狄克斯屈拉）算法的基本思想是：若起点v_s到终点v_t的最短路经过点v₁、v₂、v₃，则v₁到v_t的最短路是p_1t={v₁，v₂，v₃，v_t}，v₂到v_t的最短路是p_2t={v₂，v₃，v_t}，v₃到v_t的最短路是p_3t={v₃，v_t}。具体计算是在图上进行一种标号迭代的过程。

设弧（i，j）的长度为c_ij≥0，v_i到v_j的最短路记为p_ij，最短路长记为L_ij。

点标号：b（j）表示起点v_s到点v_j的最短路长（距离），网络的起点v_s标号为b（s）=0。

弧标号：k（i，j）=b（i）+c_ij。

则Dijkstra算法的基本步骤为：

1）找出所有起点v_i已标号终点v_j未标号的弧，集合为B={（i，j）|v_i已标号；v_j未标号}，如果这样的弧不存在或v_t已标号则计算结束。

2）计算集合B中弧的标号：k（i，j）=b（i）+c_ij。

3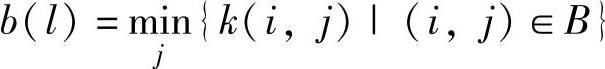），在弧的终点v_l标号b（l），返回步骤1）。

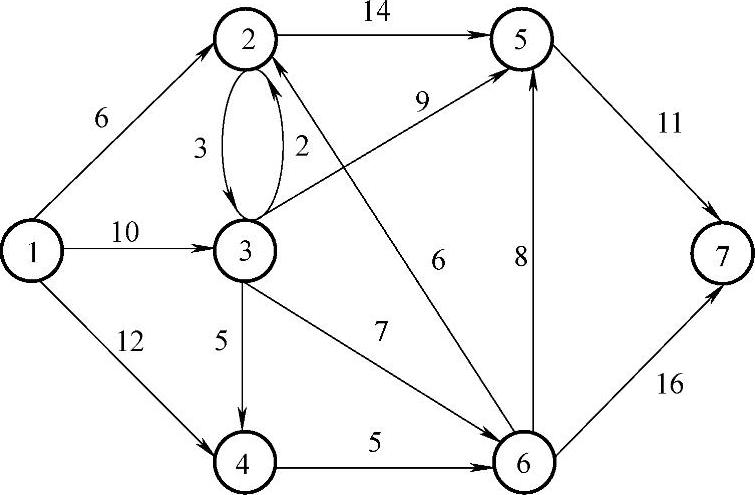
图7-7

完成步骤1）～3）为一轮计算，每一轮计算至少得到一个点的标号，最多通过n（图的点数）轮计算得到最短路。

【例7.3】 图7-7所示为某地区七个城镇间的公路交通网。城镇1有一批货物需运往城镇7。网络边上的数据为综合运输费用，问如何选择路线，才能使总的综合费用最少。

解 这是一个最短路问题，下面用Dijk-stra算法来求解这一问题。

首先给起点v₁标号b（1）=0。

第一轮标号：起点已标号、终点未标号的弧集合：B={（1，2），（1，3），（1，4）}，k（1，2）=b（1）+c₁₂=0+6=6，k（1，3）=0+10=10，k（1，4）=0+12=12，将弧的标号用圆括号填在弧上。

min{k（1，2），k（1，3），k（1，4）}=min{6，10，12}=6

k（1，2）=6最小，在弧（1，2）的终点v₂处标号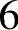，见图7-8a。

第二轮标号：在图7-8a中，起点已标号，终点未标号的集合B={（1，3），（1，4），（2，3），（2，5）}，k（1，3）与k（1，4）在第一轮中已计算，k（2，3）=6+3=9，k（2，5）=6+14=20，对弧（2，3）及（2，5）标号。

min{k（1，3），k（1，4），k（2，3），k（2，5）}=min{10，12，9，20}=9(www.daowen.com)

k（2，3）=9最小，在弧（2，3）的终点v₃处标号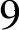，见图7-8b。注意，这里弧（3，

2）不在集合B中。

第三轮标号：在图7-8b中，起点已标号，终点未标号的集合B={（1，4），（2，5），（3，4），（3，5），（3，6）}，k（1，4）与k（2，5）在前两轮已计算，k（3，4）=9+5=14，k（3，5）=9+9=18，k（3，6）=9+7=16，对弧（3，4）、（3，5）及（3，6）标号。

min{k（1，4），k（2，5），k（3，4），k（3，5），k（3，6）}=min{12，20，14，18，16}=12k（1，4）=12最小，在弧（1，4）的终点v₄处标号，见图7-8c。

第四轮标号：在图7-8c中，起点已标号，终点未标号的集合B={（2，3），（2，5），（3，6），（4，6）}，k（2，5）、k（3，5）、k（3，6）在前面已计算，k（4，6）=12+5=17，k（3，5）=9+9=18，对弧（4，6）标号。

min{k（2，5），k（3，5），k（3，6），k（4，6）}=min{20，18，16，17}=16

k（3，6）=16最小，在弧（3，6）的终点v₆处标号，见图7-8d。

第五轮标号：在图7-8d中，起点已标号，终点未标号的集合B={（2，5），（3，5），（6，5），（6，7）}，k（2，5）与k（3，5）在前面已计算，k（6，5）=16+8=24，k（6，7）=16+16=32，对弧（6，5）及（6，7）标号。

min{k（2，5），k（3，5），k（6，5），k（6，7）}=min{20，18，24，32}=18

k（3，5）=18最小，在弧（3，5）的终点v₅处标号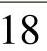，见图7-8e。

第六轮标号：在图7-8e中，起点已标号，终点未标号的集合B={（6，5），（6，7）}，k（6，7）=32，k（5，7）=18+11=29，对弧（5，7）标号。

min{k（6，7），k（5，7）}=min{32，29}=29

k（5，7）=29最小，在弧（5，7）的终点v₇处标号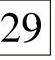，见图7-8f。

到此，所有节点均标上了标号，算法停止。可见，从城市1到城市7的最小运费为29个单位。

用Dijkstra算法求解最短路问题要注意一下问题：

1）Dijkstra算法的条件是弧长非负，问题求最小值。

2）Dijkstra算法求得的最短路线可能不唯一，但最短路长相等。

3）Dijkstra算法可以求任意两点之间的最短路（最短路存在），只要将两个点看做路线的起点和终点，然后进行标号。

图7-8f中的每个点都得到标号，说明v₁到其他各点的最短路都已经找到，如v₁到v₆的最短路是p₁₆={v₁，v₂，v₃，v₆}，最短路长为16。