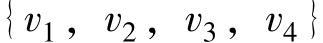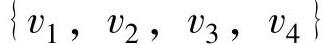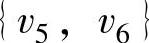在一个连通图G中，取部分边连接G的所有点组成的树称为G的部分树或支撑树（Spanning Tree）。图7-3是图7-2的部分树。图7-4中三个图都不是图7-2的部分树。要想称为部分树首先必须是一棵树，而图7-4a中形成一个圈，不是一棵树，图7-4b中与之间不连通，也不是一棵树，图7-4c没有包含点v₁。

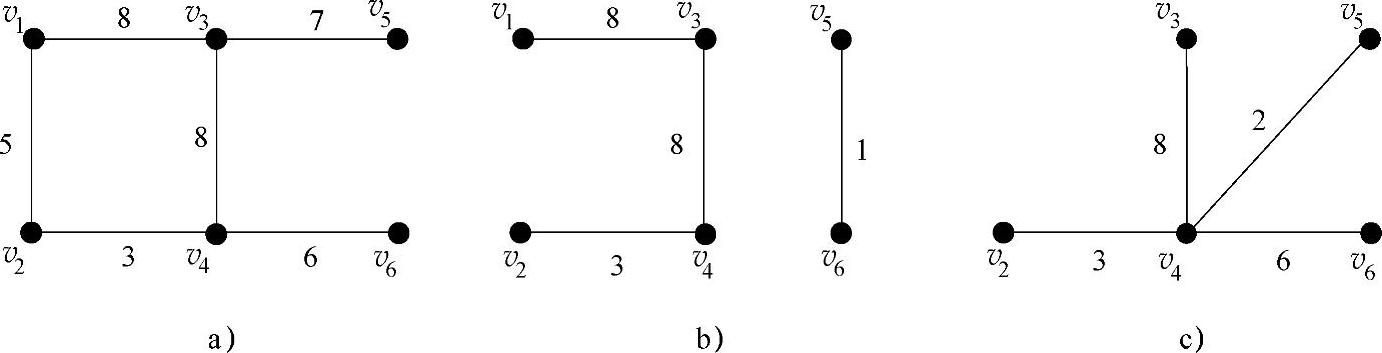
图7-4

应当注意的是：任意一个连通图G中一定存在部分树。

定义网络图G的部分树T的长度等于T中每条边的长度之和，记为G（T）。则令该图G=（V，E），对于每一条边e=[V_i，V_j]，有一权W_ij≥0，表示每条边的长度，最小树问题就是求赋权图G的部分树T，使得：

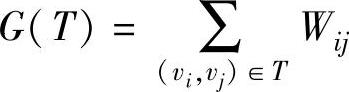
取最小值。

最小树问题就是要求给定连通赋权图G的最小树。

假设给定一些城市，已知每对城市间交通线的建造费用。要求建造一个连接这些城市的交通网，使总的建造费用最小，这个问题就是赋权图上的最小树问题。

最小部分树可以直接用作图的方法求解，常用的有避圈法和破圈法两种方法。

(www.daowen.com)

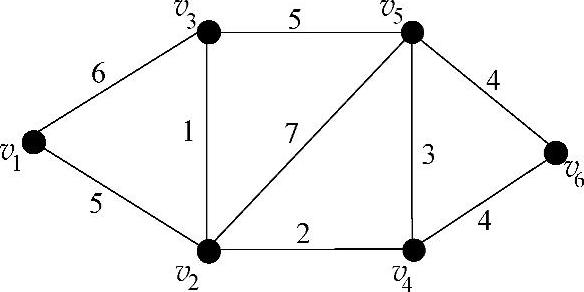
图7-5

避圈法：取图G的n个孤立点（v₁，v₂，…，v_n）作为一个支撑图，开始选一条最小权的边，以后每一步中，总是从与已选边不构成圈的那些未选边中，选一条权最小的边，直到连通（有n-1条边）。

【例7.1】 某六个城市的道路网如图7-5所示。

已知每条道路的长度，要求沿着路架修建连接这六个城市的公路网，使公路网长度最小。

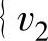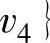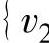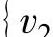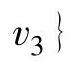解 去掉所有边得到支撑图7-6a。首先添加最短边{v₂，v₃}，再添加次短边，（同时保证{v₂，v₄}与，不构成圈），再从剩下的边中选择与，和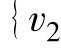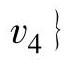，不构成圈的最短边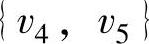，依次进行下去，得到的最小树如图7-6b所示

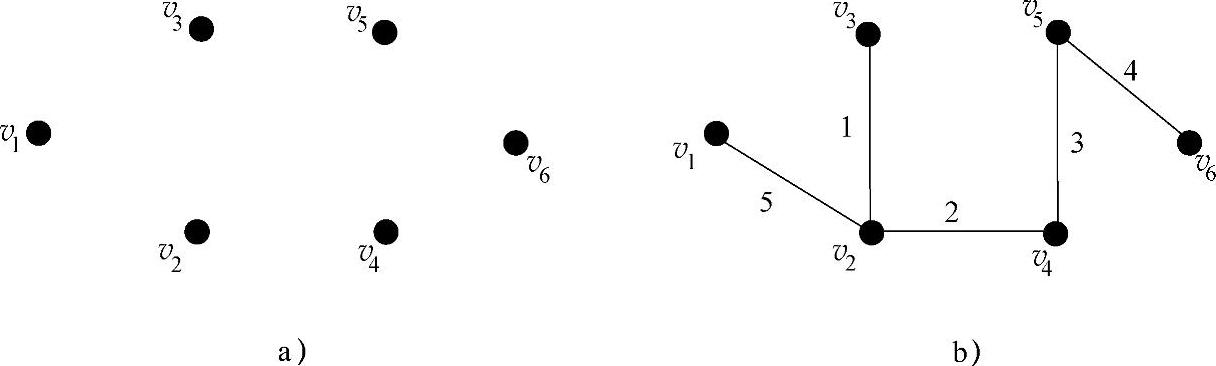
图7-6

破圈法：取图G中任意一个圈，从圈中去掉一条权最大的边（如果有两条或两条以上的边都是权最大的边，则任意去掉其中一条）。在余下的图中，重复这个步骤，直到得到一个不含圈的图为止，这时的图便是最小树。

【例7.2】 用破圈法求例7.1的最小树。

解 在图7-5中任意取一个圈，如{v₁，v₂，v₃，v₁}，去掉最长边{v₁，v₃}；在去掉边{v₁，v₃}的图中再取圈{v₃，v₅，v₂，v₃}，去掉最长边{v₂，v₅}；在去掉边{v₁，v₃}和{v₂，v₅}的图中再取圈{v₅，v₆，v₄，v₅}，这个圈中{v₅，v₆}和{v₄，v₆}都是权最大的边，去掉其中的一条，比如去掉{v₄，v₆}，这时得到的最小树如图7-6b所示。