图与网络理论在系统分析中占有重要的地位。在实际工程中,许多工程系统都可以用图形来描述,如第4章例4.1的运输问题和例4.13的配置问题。因此,可以把一个工程系统的各种物理量之间的关系用一个抽象的图或网络模型来描述,利用图与网络的某些性质求解网络模型往往要比求解数学模型简单很多。
运筹学中研究的图具有下列特征:
1)用点表示研究对象,用边(有方向或无方向)表示对象之间某种关系。
2)强调点与点之间的关联关系,不讲究图的比例大小、形状以及位置等。
3)每条边上都赋有一个权,其图称为赋权图。实际中权可以代表两点之间的距离、费用、利润、时间、容量等不同的含义。
4)建立一个网络模型,求最大值或最小值。
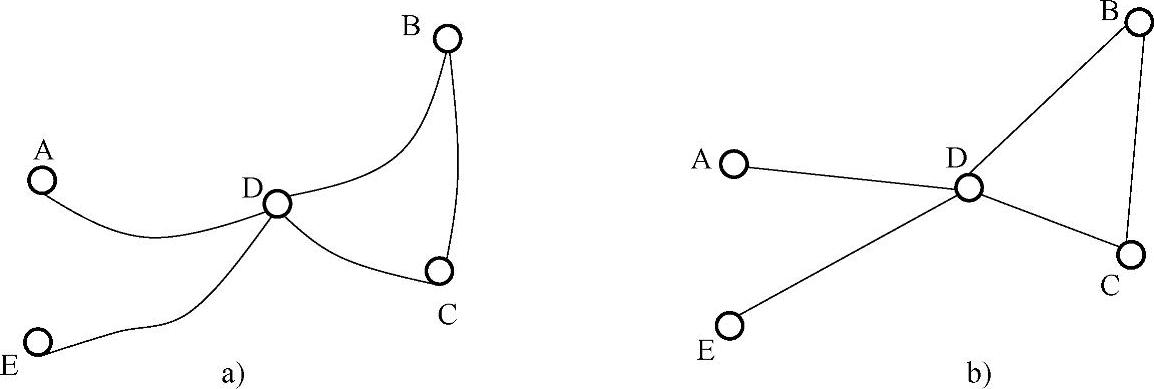
下面以实例来说明图在道路交通中的应用。图7-1a表示某地区的公路交通网,A、B、C、D、E表示五个城镇,A、B、C、D、E之间的连线表示两城镇间的公路,我们研究的问题就是“两城镇间有无公路相通”这一特定关系,那么就可以用图7-1b点的网状图来代替图7-1a的公路交通图。
 (https://www.daowen.com)
(https://www.daowen.com)
图7-1
可以定义:图是顶点和边的集合,记为G=(V,E),连通的赋权图称为网络图,记为G=(V,E,W),其中V代表点集合,E代表边集合,W为权值。如图7-2所示,点集合记为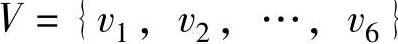 ,边用[vi,vj]表示或简记为[i,j],边集合记为
,边用[vi,vj]表示或简记为[i,j],边集合记为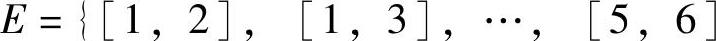 },边上的数字称为权,记为w[vi,vj]、w[i,j]或wij,权集合记为
},边上的数字称为权,记为w[vi,vj]、w[i,j]或wij,权集合记为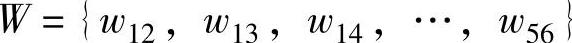 。
。
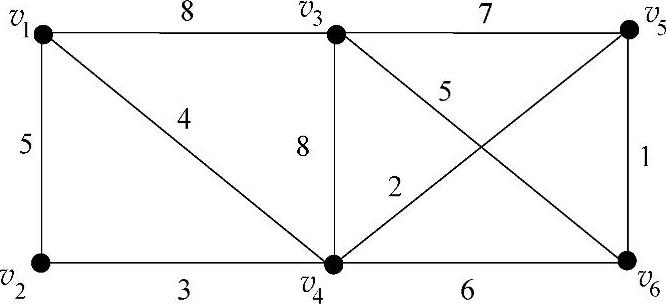
图7-2
给定一个图G,若任何两点之间至少有一条链,则称这个图为连通图。若一个图不是连通图,则它的每个连通的部分称为该图的一个连通分图(简称分图)。图7-1b是一个不连通图,但它有一个连通分图。
给定一个图G,一个点,边交错序列(vi1,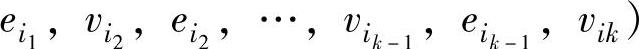 ,如果满足
,如果满足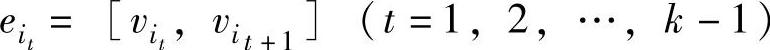 ,则称图G为一条连接
,则称图G为一条连接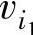 和
和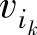 的链,记为
的链,记为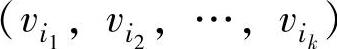 。在链(
。在链(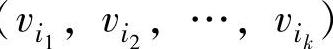 中,若
中,若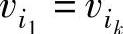 ,则称之为一个圈,记为
,则称之为一个圈,记为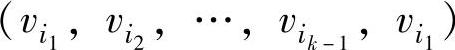 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








