【摘要】:递推方程: 有一辆最大货运量为10t的货车,用于装载三种货物,每种货物的单位重量及相应单位价值见表6-11,如何装载可使总价值最大。表6-11解 设第i种货物装载的件数为xi,则该问题可表示为:终端条件:f4=0。k=2时,递推方程为:,决策集为{0,1,2,3,4,5}。表6-13下一阶段的最优决策见表6-14。
这里用动态规划方法求解只有一个约束条件(一维背包问题)的整数规划最优解,即背包只有重量或体积限制。
问题:今有n种物品各若干,待装入容积(容重)为W的背包中。第i种物品的单件体积(重量)为wi,单件价值为ci,i=1,2,…,n,应如何确定装入背包的各种物品的数量,才能使所装入物品的总体积(重量)不超过背包的容积(容重)且总价值最大。
设xi为将第i件物品装入背包的件数,则可建立如下整数规划数学模型:
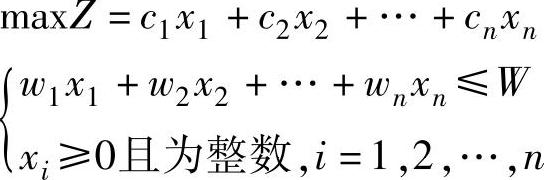
动态规划的有关要素如下:
阶段k:第k次装载第k种物品(k=1,2,…,n)。
决策变量xk:第k次装载第k种物品的件数。决策允许集合: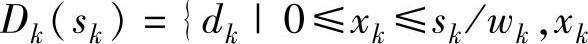 为整数}。
为整数}。
状态转移方程:sk+1=sk-wkxk。
阶段指标:vk=ckxk。
终端条件:fn+1(sn+1)=0。
递推方程:
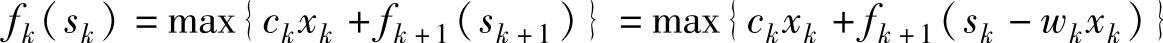
【例6.5】 有一辆最大货运量为10t的货车,用于装载三种货物,每种货物的单位重量及相应单位价值见表6-11,如何装载可使总价值最大。
表6-11

解 设第i种货物装载的件数为xi,则该问题可表示为:
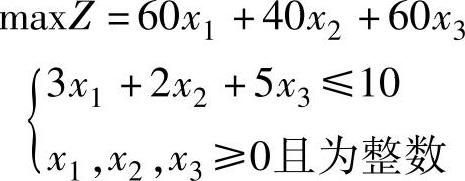
终端条件:f4(x4)=0。(www.daowen.com)
k=3时,递推方程为:
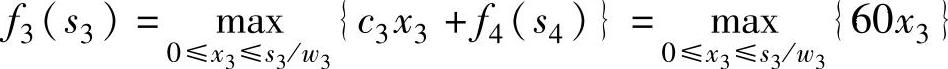
计算过程见表6-12。
表6-12

表6-12省略了部分内容,最优决策是:s3为0~4时,s3=0;s3为5~9时,x3=1,s3=10时,x3=2。
k=2时,递推方程为:
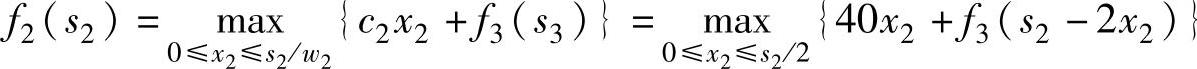
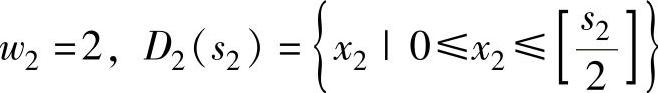 ,决策集为{0,1,2,3,4,5}。计算过程见表6-13。
,决策集为{0,1,2,3,4,5}。计算过程见表6-13。
表6-13
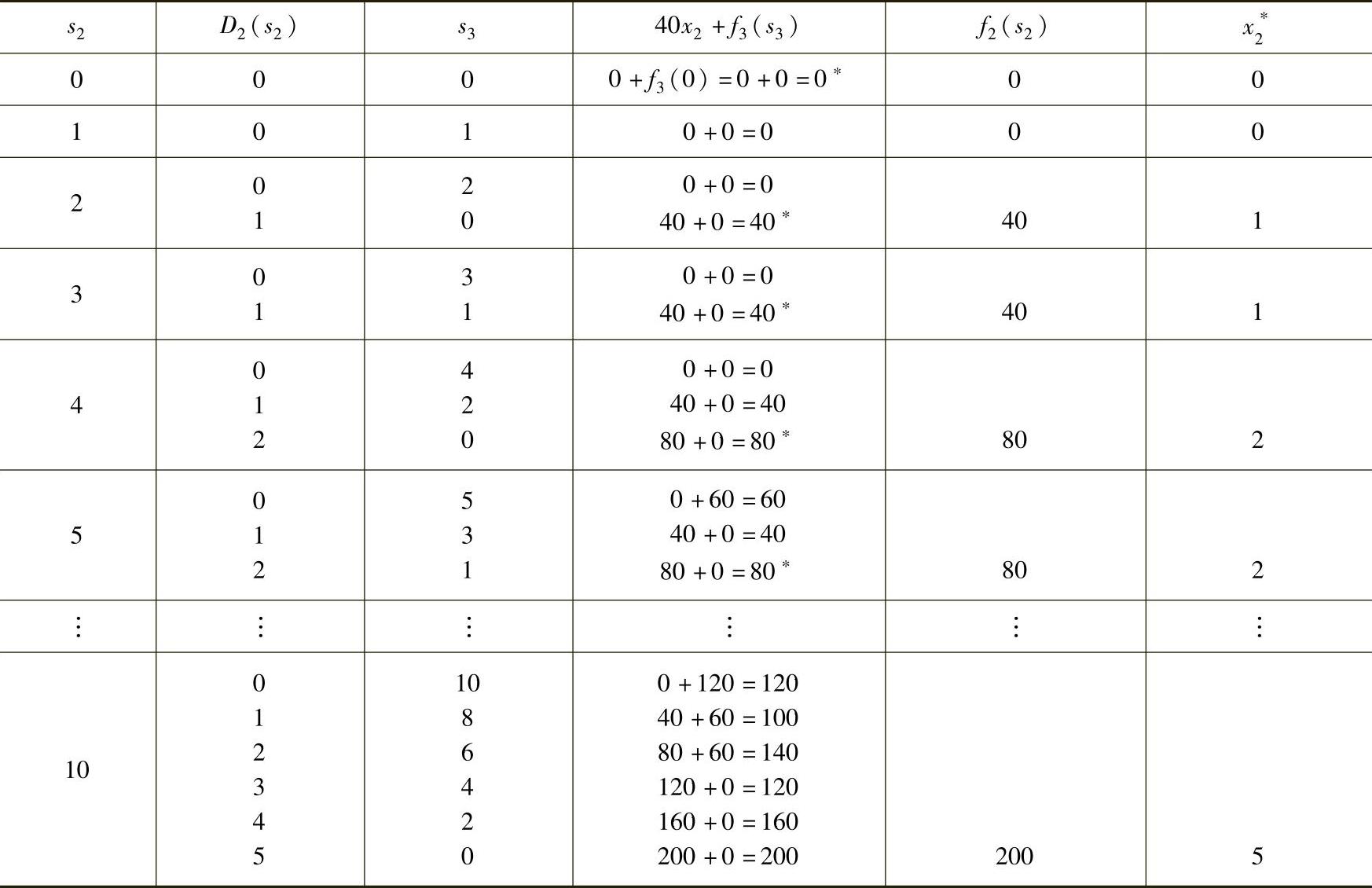
下一阶段的最优决策见表6-14。
表6-14

k=1时,递推方程为:
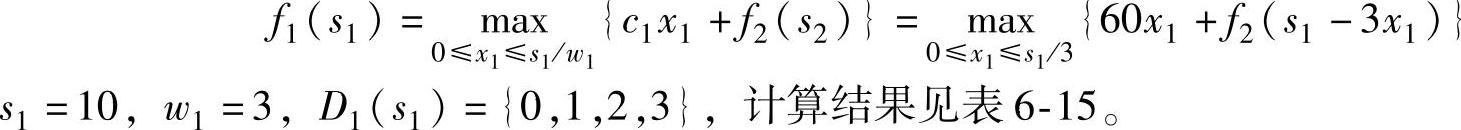
表6-15
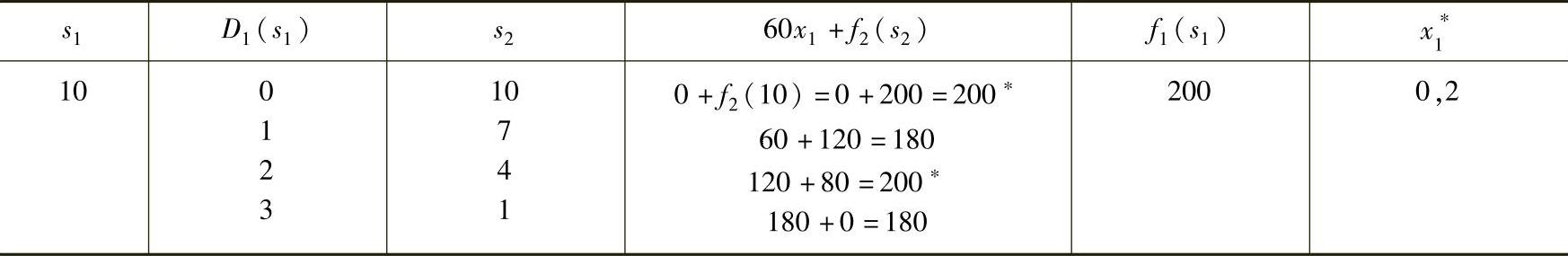
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关交通运筹学的文章








