问题:在一项具有n个时期的生产计划中,企业如何制定生产策略以确定不同时期的生产量和存储量,在满足产品需求量的条件下,使得总成本(生产成本+存储成本)最小。
设第k时期产品的生产量为Xk,生产限量为Xk;第K时期的需求量为dk;第K时期生产Xk件产品的成本为Ck(%);第矗时期开始有存储量Sk所需的存储成本为Hk(Sk);M为各期产品存储量上限,不允许缺货,存量下限非负有时也设定一个下限(安全存量),则此问题的数学模型为:
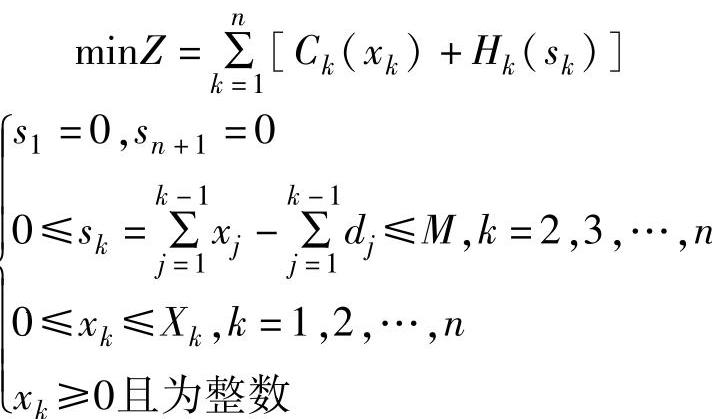
下面用动态规划方法求解此问题。将问题看做是一个n阶段决策问题,决策变量xk表示第k阶段的生产量,状态变量sk表示第k阶段开始的存储量。最优指标函数fk(sk)为第k阶段初存储量为sk时,从第k阶段到第n阶段的最小总成本。动态规划的数学模型为:
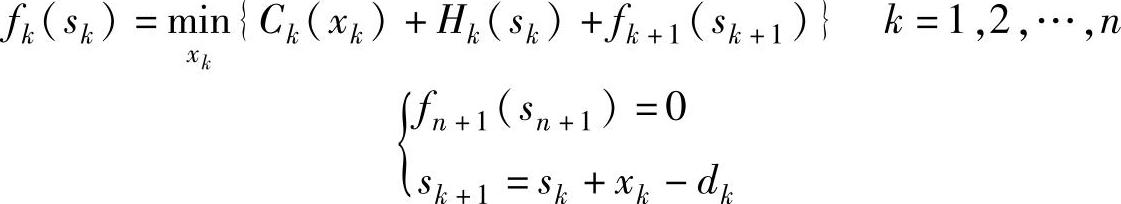
最后求出f1(s1)就是最小总成本。
【例6.4】 一个工厂生产某种产品,1~6月份生产成本和产品需求量的变化情况见表6-9。如果没有生产准备成本,单位产品一个月的存储费为hk=0.6元,月底交货,分别求下列两种情形6个月总成本最小的生产方案。
1)1月初与6月底存储量为零,不允许缺货,仓库容量为S=50件,生产能力无限制。
2)其他条件不变,1月初存量为10。
表6-9

解 动态规划求解过程如下。
阶段k:月份,k=1,2,…,7。
状态变量sk:第k个月初的存储量。
决策变量xk:第k个月的生产量。
状态转移方程:sk+1=sk+xk-dk。决策允许集合: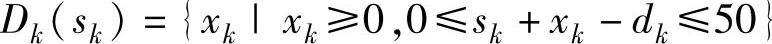 。阶段指标:
。阶段指标: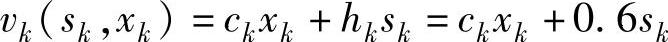 。终端条件:f7(s7)=0,s7=0。递推方程:
。终端条件:f7(s7)=0,s7=0。递推方程:
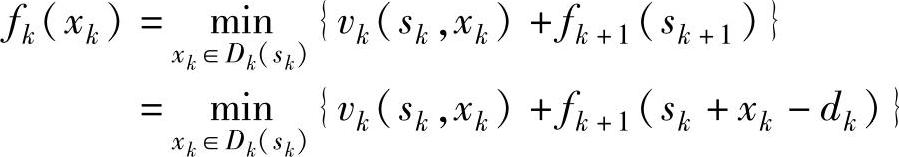
当k=6时,因为s7=0,有 ,所以:
,所以:
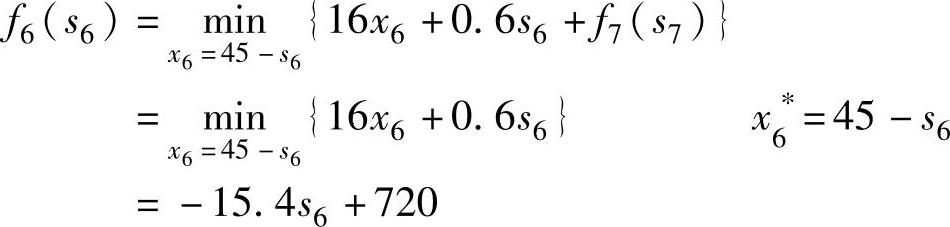
当k=5时,由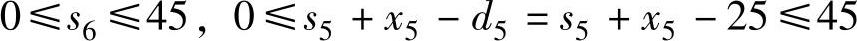 ,得
,得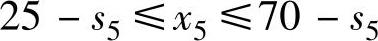 ,由于s5≤50,则当25-s5<0时x5的值取“0”,决策允许集合为:
,由于s5≤50,则当25-s5<0时x5的值取“0”,决策允许集合为:
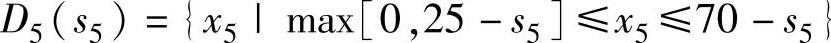
则有:
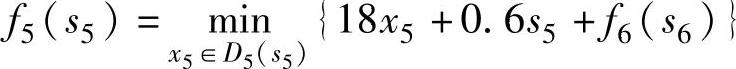
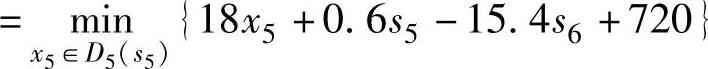
(其中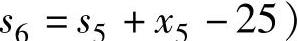
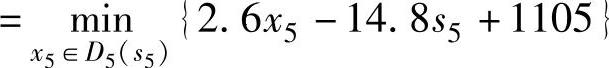 s5≤25时,取下界:
s5≤25时,取下界: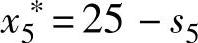 s5>25时,取下界:
s5>25时,取下界: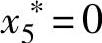
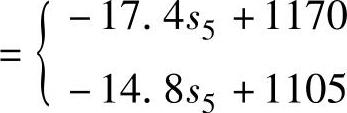 (www.daowen.com)
(www.daowen.com)
k=4时,0≤s5≤25,0≤s4+x4-40≤25,有40-s4≤x4≤65-s4,决策允许集合为:
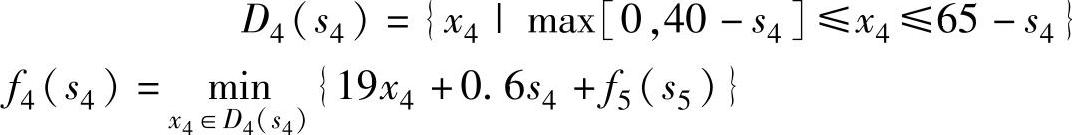
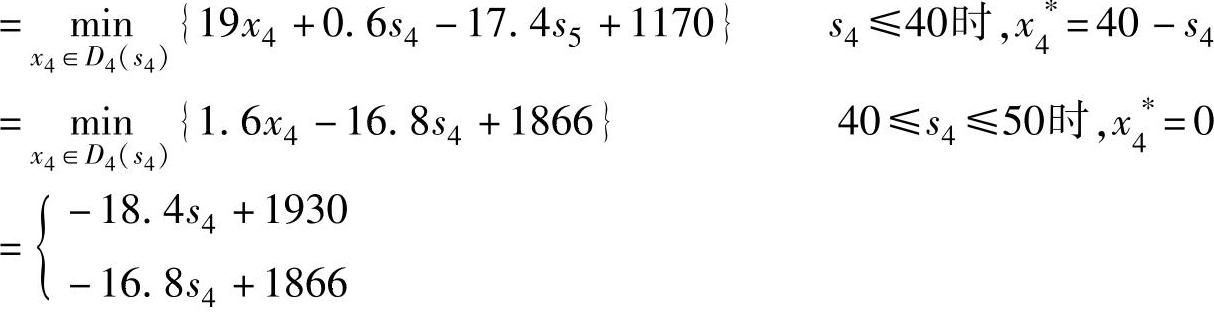
当25<s5≤50,x5=0,25≤s4+x4-40≤50,有:
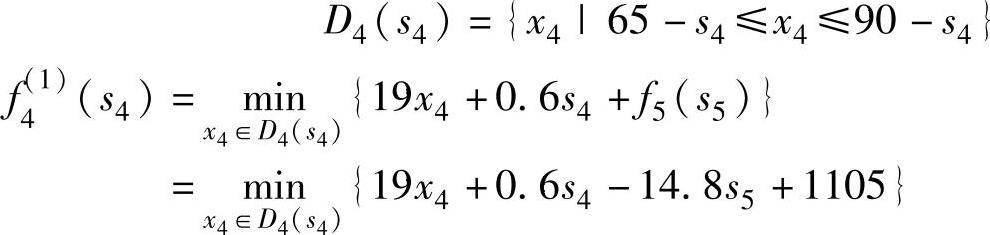
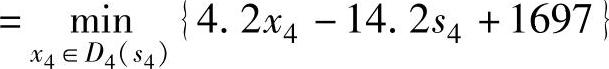 取下界:
取下界: =-18.4s4+1970
=-18.4s4+1970
显然该决策不可行,x5=0,s4+x4=65=d4+d5,s5=s4+x4-d4=25,与s5>25矛盾。因此有:
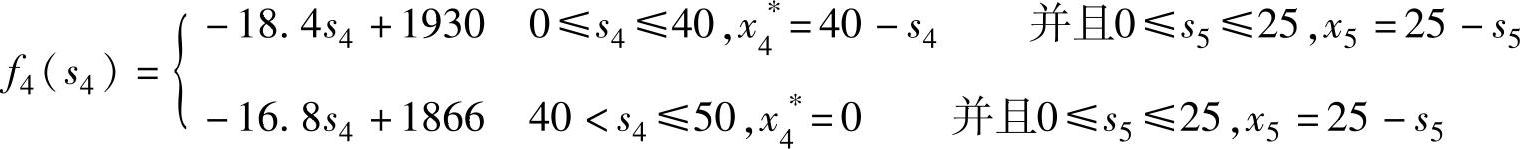
k=3时,0≤s4≤40,0≤s3+x3-35≤40,有:
D3(s3)={x3|max[0,35-s3]≤x3≤75-s3}
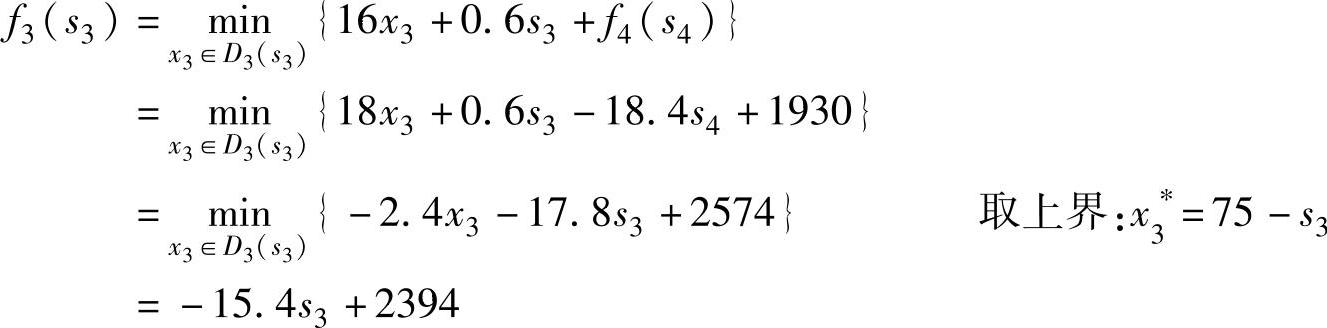
当40≤s4≤50时,40≤s3+x3-35≤50,有:
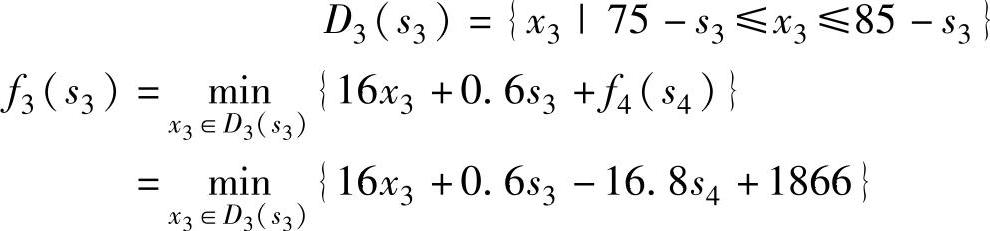
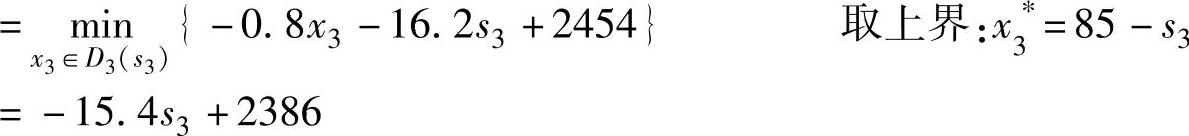
取决策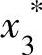 =85-s3,f3(s3)=-15.4s3+2386
=85-s3,f3(s3)=-15.4s3+2386
k=2时,由40≤s4≤50,0≤s3≤50,0≤s2+x2-30≤50,有30-s2≤x2≤80-s2,x2的决策允许集合为:
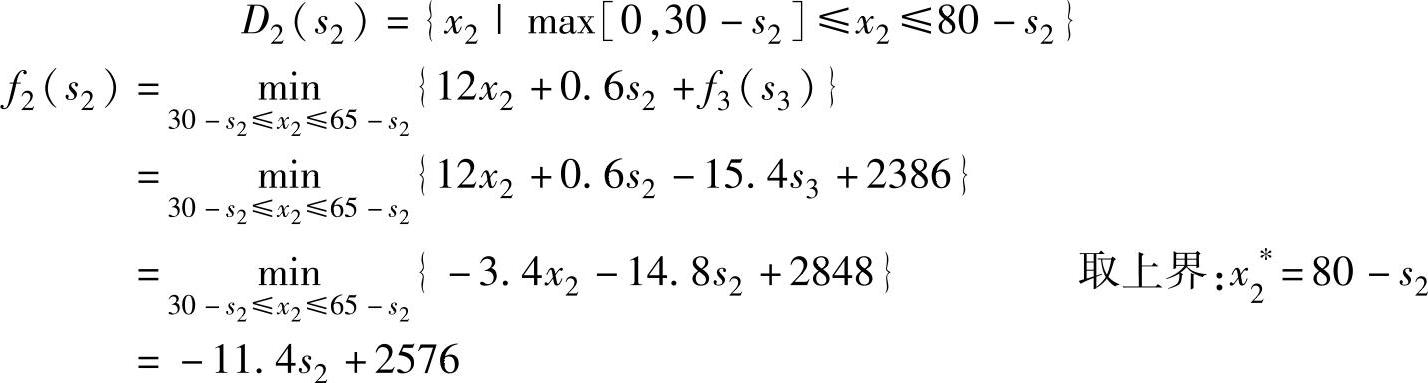
k=1时,由0≤s2≤50,0≤s1+x1-20≤50,20-s1≤x1≤70-s1,只要期初存储量s1≤20,则x1的决策允许集合为:
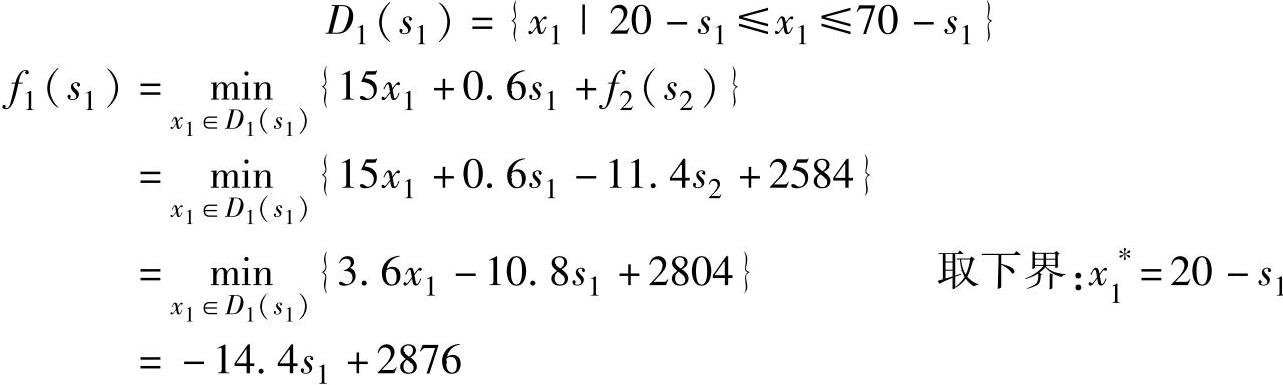
1)期初存储量s1=0,由各阶段的最优决策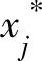 及状态转移方程,回溯可求出最优策略。x1=20,s2=s1+x1-d1=0+20-20=0,x2=80,s3=s2+x2-d2=0+80-30=50,x3=85-50=35,s4=s3+x3-d3=50+35-35=50>40,x4=0,s5=50-0-40=10<25,x5=25-s5=15,s6=10+15-25=0,x6=45。总成本为2876。1~6月份生产与储存详细计划见表6-10。
及状态转移方程,回溯可求出最优策略。x1=20,s2=s1+x1-d1=0+20-20=0,x2=80,s3=s2+x2-d2=0+80-30=50,x3=85-50=35,s4=s3+x3-d3=50+35-35=50>40,x4=0,s5=50-0-40=10<25,x5=25-s5=15,s6=10+15-25=0,x6=45。总成本为2876。1~6月份生产与储存详细计划见表6-10。
表6-10
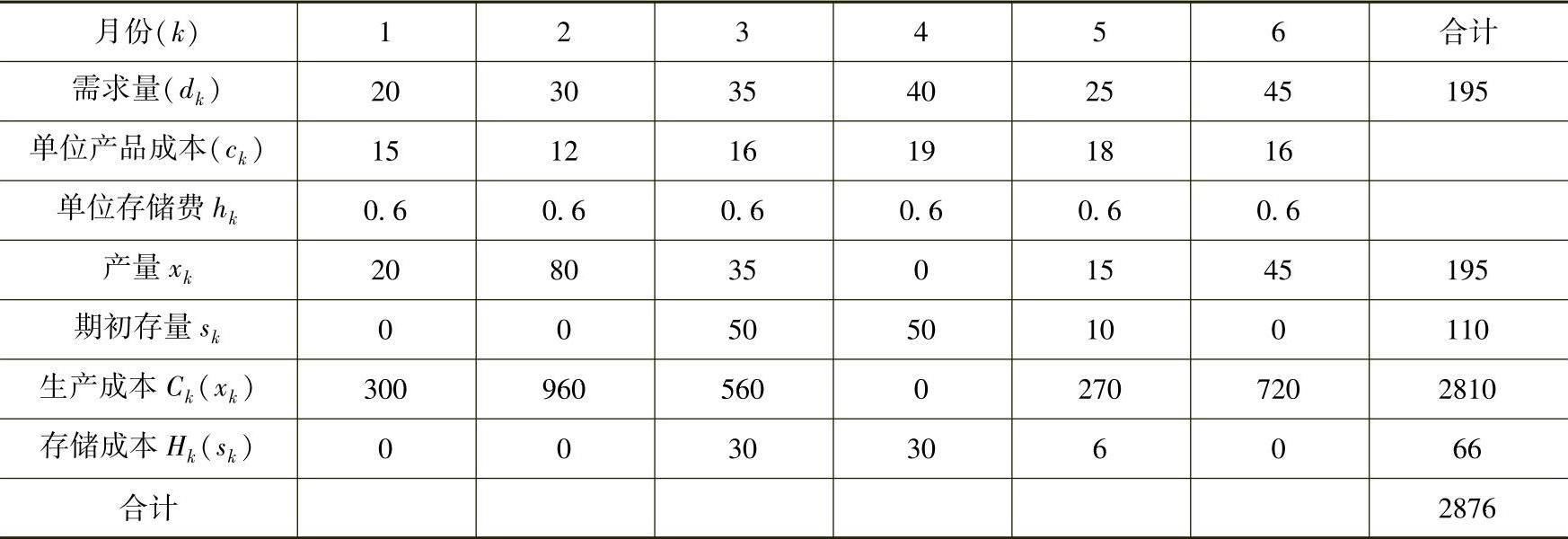
2)期初存储量s1=10,与前面计算类似,得到x1=10,x2=80,x3=35,x4=0,x5=15,x6=45。
在实际生产过程中,问题可能比例6.4复杂得多。例如,各期的变动成本和存储成本是一个函数式,甚至是非线性函数,各期有不同的生产量和存储量限制,允许延期交货但要支付缺货费用等情形。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






