问题:拟将总量为c的某种资源投入到方式为A、B的两种生产中去。将数量为x、y的资源分别用于生产方式A、B可获收益g(x)、h(y),并可分别以回收率a、b回收部分资源用于下一个阶段的再生产,其中g、h为已知函数,且g(0)=h(0)=0,生产过程分n个阶段连续进行,如何分配资源用于这n个阶段的生产才能使总收益最大。
设在第i个阶段用于方式A的资源的数量为xi,i=1,2,…,n,则可建立如下数学规划模型:
这是一个多阶段决策问题,可利用动态规划方法来求解。
【例6.3】 某工厂计划将1000台机器分配到A、B两个车间。分配x、y台机器到车间A、B的年收益分别为g(x)=8x,h(y)=5y,回收率分别为a=0.7、b=0.9。试制定该厂5年间总收益最大的机器分配方案。
解 动态规划求解过程如下。
阶段k:运行年份(k=1,2,…,6),k=1表示第1年年初,k=6表示第5年年末(即第6年年初)
状态变量sk:第k年年初完好的机器数(k=1,2,…,6),也是第k-1年年末完好的机器数,其中s6表示第5年年末(即第6年年初)的完好机器数,s1=1000。
决策变量xk:第k年年初投入A车间的机器数。
状态转移方程: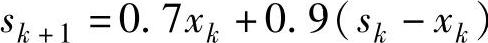 。决策允许集合:
。决策允许集合: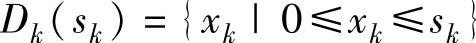 。阶段指标:
。阶段指标: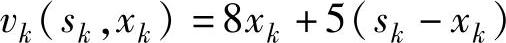 。终端条件:f6(s6)=0。递推方程:
。终端条件:f6(s6)=0。递推方程:
fk(xk)表示第k年年初分配xk台设备用于高负荷生产时到第5年年末的最大产量,计算过程如下:(https://www.daowen.com)
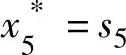 时最优
时最优
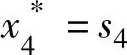 时最优
时最优
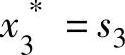 时最优
时最优
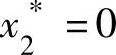 时最优
时最优
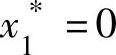 时最优
时最优
因为sl=1000,5年的最大总产量为f1(s1)=23.6912x1000=23691.2。
由于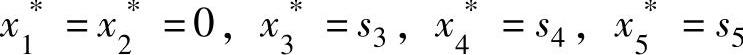 ,机器的最优分配策略为:前两年将拥有的机器全部分配到B车间,后三年将拥有的机器全部分配到A车间。
,机器的最优分配策略为:前两年将拥有的机器全部分配到B车间,后三年将拥有的机器全部分配到A车间。
一般地,设一个周期为n年,A公司生产时设备的完好率为倪,单台产量为g;B公司生产时设备的完好率为6,单台产量为h。若有t满足:
则最优设备分配策略是:在1-t-1年,年初将全部完好设备投入低负荷运行,在t-n年,年初将全部完好设备投入高负荷运行,总产量达到最大。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




