例6.1的最短路问题具有以下特征：

1）问题具有多阶段决策的特征。

2）每一阶段都有相应的“状态”与之对应。

3）每一阶段的某个状态都面临有若干个决策，选择不同的决策将会导致下一阶段不同的状态，同时，不同的决策将会导致这一阶段不同的距离。如图6-2所示的第1阶段状态v₁，其决策是到达下一阶段点的选择。状态v₁有3种选择，决策允许集合为{v₂，v₃，v₄}，也是第2阶段的状态集合。又如第2阶段状态v₃，到下一阶段的选择有v₅和v₆，决策允许集合为{v₅，v₆}。同一阶段各状态的决策集合可能相同也可能不同。

4）每一阶段的最短路长（最优解）问题可以递推地归结为下一阶段各个可能状态的最优解问题，各子问题与原问题具有完全相同的结构。

动态规划解决问题的关键是将问题归结为一个递推过程，建立一个递推指标函数求最优解。如果不能建立递推函数则动态规划方法无效。

图6-2的递推指标函数为：

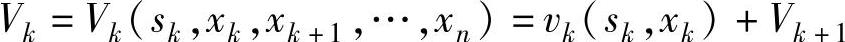
最优指标函数为：

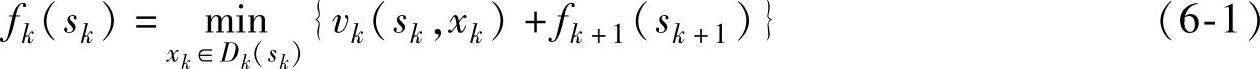
式中，f_k（s_k）为阶段k状态为s_k时到终点v₁₀的最短距离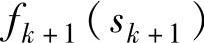；为k+1阶段状态为s_k+1到终点v₁₀的最短距离；v_k（s_k，x_k）是状态为s_k选择决策x_k时，s_k到x_k的距离；D_k（s_k）为状态s_k的决策集合。

式（6-1）是动态规划的基本方程或称为最优性方程。

当求出k+1阶段各状态的最优解（到终点的最短距离），利用式（6-1）就可以求出第k阶段各状态的最优解，依次类推，最后求出第1阶段状态v₁的最优解（v₁到v₁₀的最短距离）。

式（6-1）的递推关系理解为：阶段k状态为s_k到终点v₁₀的最短距离归结为该状态选择决策x_k后的距离v_k（s_k，x_k）加上x_k到v₁₀的最短距离求最小值。例如求v₃到v₁₀的最短距离f₂（v₃）为：

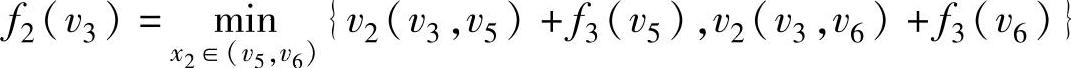
动态规划基本原理是将一个问题的最优解转化为求子问题的最优解，研究的对象是决策过程的最优化，其变量是流动的时间或变动的状态，最后达到整体最优。

式（6-1）还描述了动态规划的最优性原理：如果点x_k到终点v₁₀的最短路线通过点v_k+1，则点v_k+1到终点v₁₀的最短路线也在这条路线上。

动态规划求解可分为三个步骤：分解、求解与合并。

动态规划要求子过程指标满足递推关系：

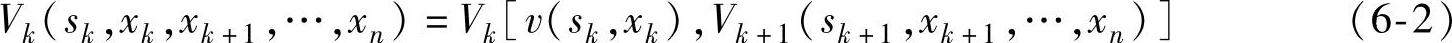
常用的指标函数有连和形式和连乘形式。连和形式为：

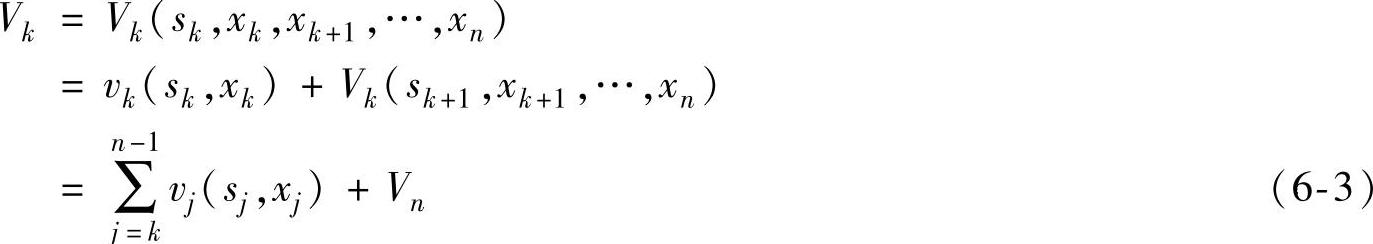
连乘形式为（v_j≠0）：

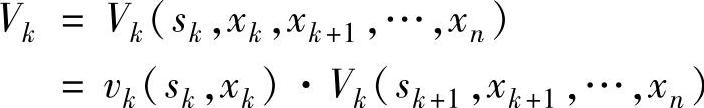
例6.1的指标函数属于连和形式。

最优指标函数f_k（s_k）是取式（6-3）或式（6-4）的最优值。式（6-3）的最优指标函数是：

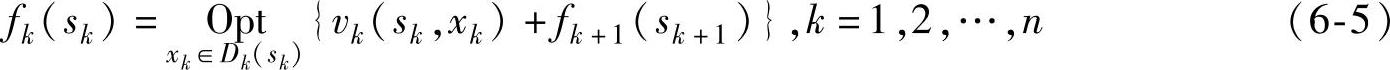
式（6-4）的最优指标函数是：

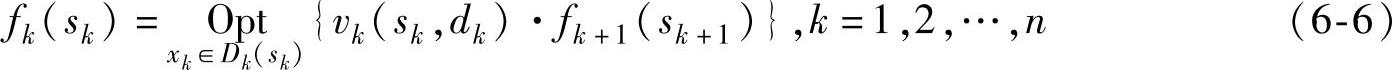
式中Opt=optimization，表示“max”或“min”。式（6-3）～式（6-6）就是动态规划的基本方程。为了使递推方程有递推起点，需要确定最后一个状态s_n的最优指标f_n（s_n）的值，称f_n（s_n）为终端条件。一般情况下，连和形式f_n（s_n）=0，连乘形式f_n（s_n）=1。但也有例外，如式（6-3）和式（6-4）中的V_n不等于0或1。在图6-2中，添加一个阶段5，终端条件是终点v₁₀到v₁₀的距离，即f₅（s₅）=0。

动态规划数学模型由式（6-5）或式（6-6）、边界条件及状态转移方程构成。如连和形式的数学模型为：

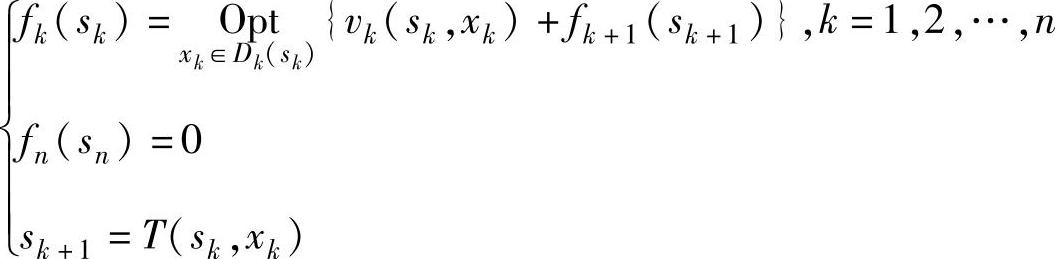(www.daowen.com)

由式（6-5）和式（6-6）的形式知，计算顺序是从最后一个阶段开始到第一阶段结束，这种方法称为逆序法。也可以将基本方程改为向前递推，如式（6-1）改为：

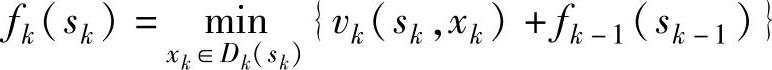
当计算顺序是从第一阶段开始到最后一个阶段结束，这种方法称为顺序法。

现在用逆序法列表求解例6.1。

k=n=5时，f₅（v₁₀）=0，k=4，递推方程为：

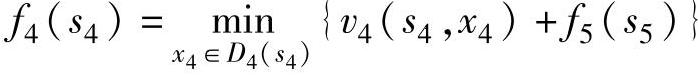
f₅（s₅）到f₄（s₄）的递推过程见表6-1。

表6-1

第4阶段各状态的决策唯一，最优值等于对应的距离。

k=3，递推方程为：

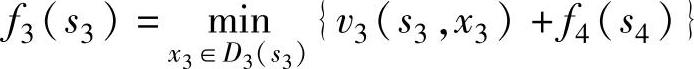
f₄（s₄）到f₃（s₃）的递推过程见表6-2。

表6-2

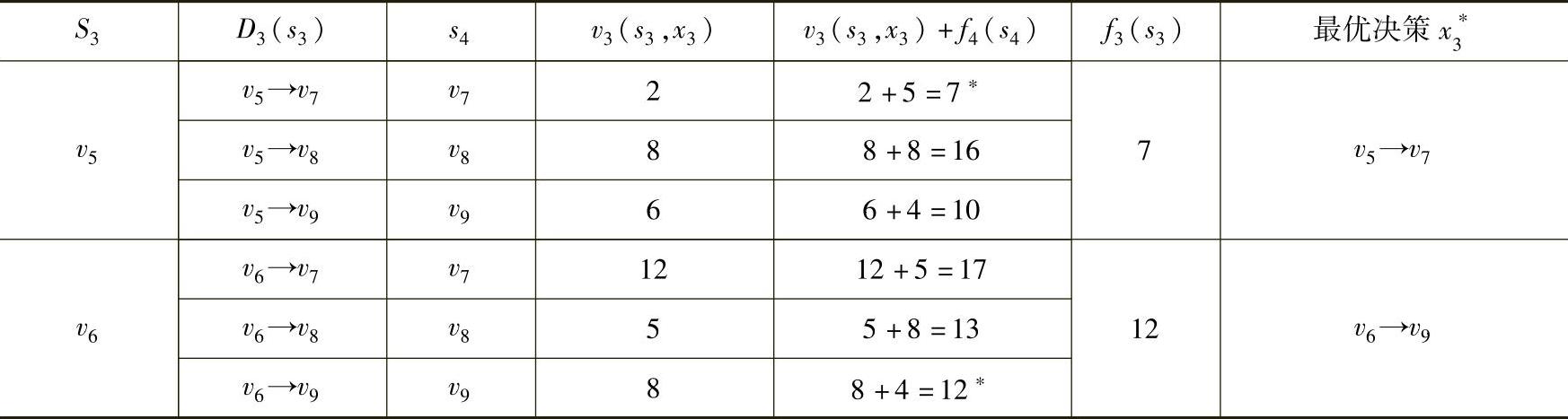
k=2，递推方程为：

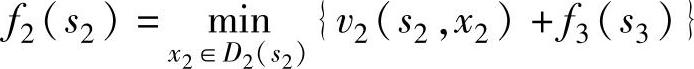
f₃（s₃）到f₂（s₂）的递推过程见表6-3。

表6-3

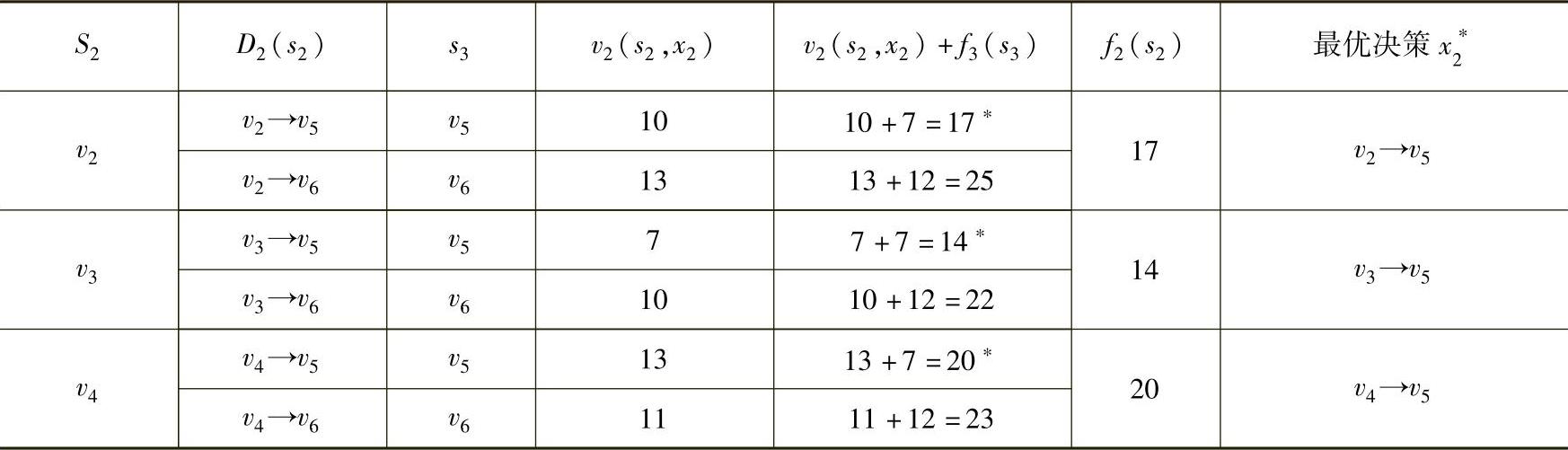
k=1，递推方程为：

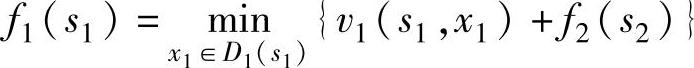
f₂（s₂）到f₁（s₁）的递推过程见表6-4。

表6-4

第1阶段计算结束，表明已得到最优策略，最优值是表6-4中f₁（s₁）的值，从v₁到v₁₀的最短路长为19。最短路线从表6-4到表6-1回溯，查看最后一列最优决策，得到最短路径v₁→v₂→v₅→v₇→v₁₀。

直接在图上计算更为简单，如图6-3所示。

应当注意的是：动态规划是一种求解思路，注重决策过程，而不是一种算法。不同的问题得到的模型也不一样。学习动态规划就是要掌握它的这种原理和思路，分析问题的条件，

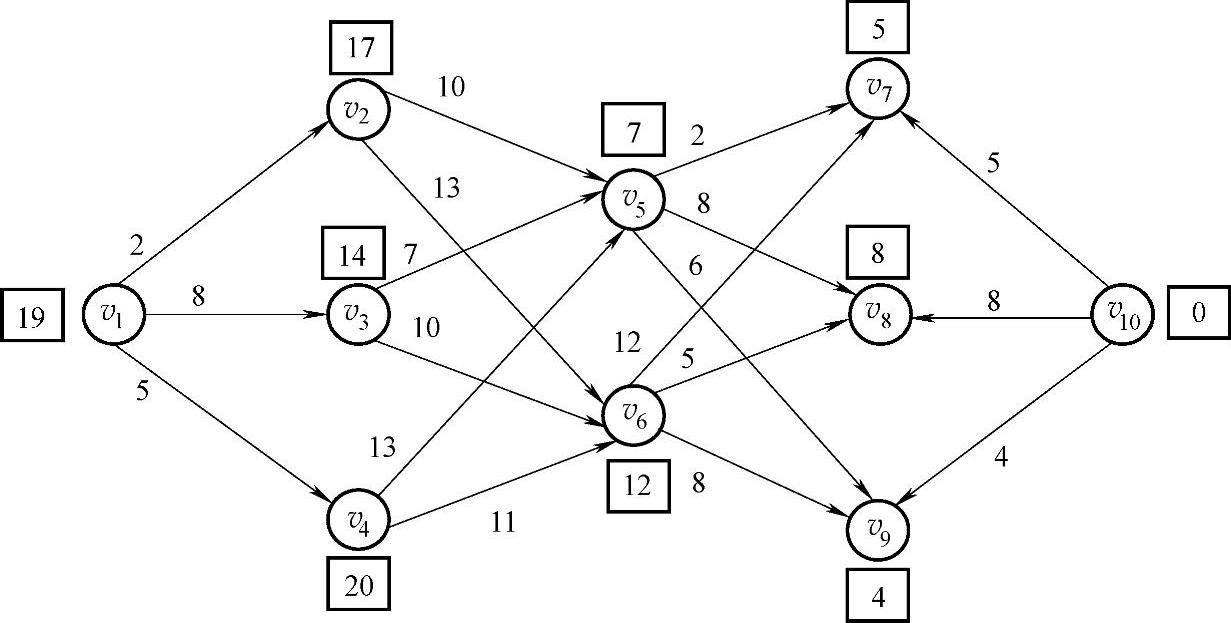
图6-3

确定模型的五个要素，利用递推关系求最优解。