【例6.1】 如图6-2所示，弧边上的数为两点间的距离，求点v₁到v₁₀的最短路线及最短路长，这是动态规划中一个较为直观的典型例子。

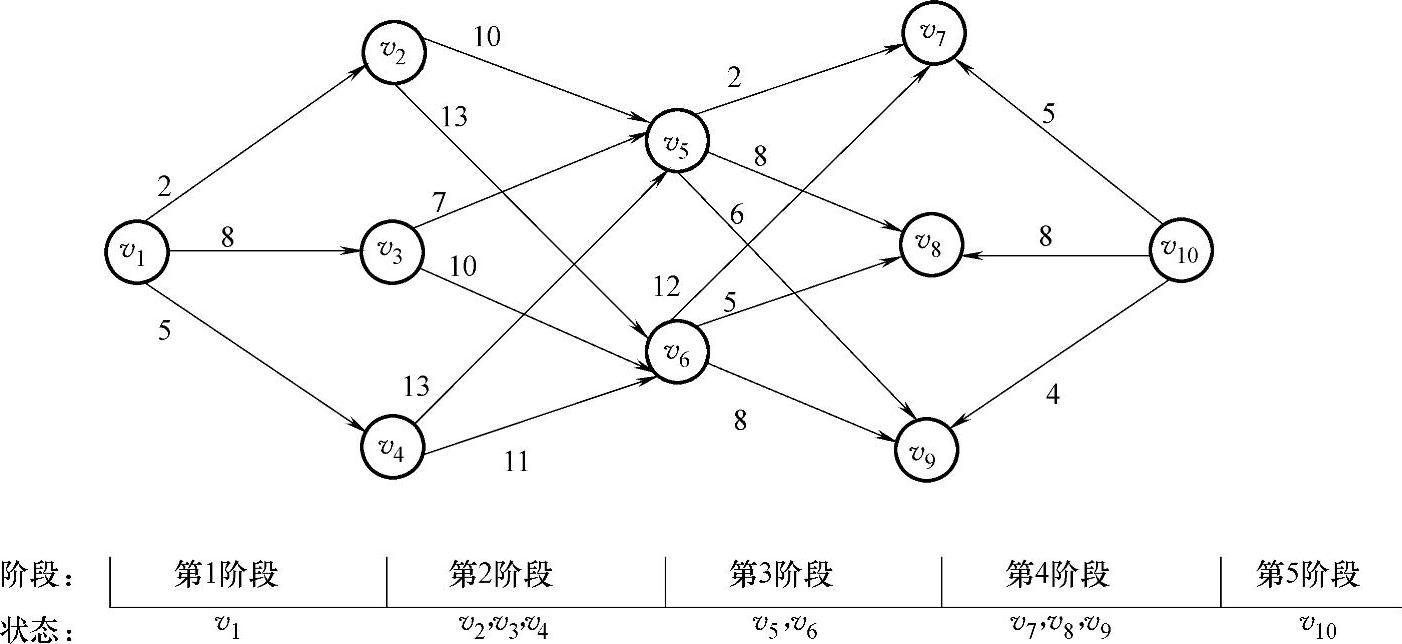
图6-2

通过该例题，我们来介绍有关动态规划的基本概念。

动态规划数学模型由阶段、状态、决策与策略、状态转移方程及指标函数5个要素组成。

（1）阶段（Stage） 表示决策顺序的时间序列，阶段可以按时间或空间划分，阶段数k可以是确定数、不定数或无限数。

图6-2中按空间划分为4个阶段，图中第5个阶段是虚拟的一个边界阶段。

（2）状态（State） 描述决策过程当前特征并且具有无后效性的量。状态可以是数量，也可以是字符，数量状态可以是连续的，也可以是离散的。每一状态可以取不同值，状态变量记为s_k。各阶段所有状态组成的集合称为状态集。

如图6-2所示，各阶段的状态为上一阶段的结束点，或该阶段的起点组成的集合。第1阶段的状态为v₁，第2阶段的状态为v₂、v₃、v₄，第3阶段的状态为v₅、v₆，第4阶段的状态为v₇、v₈、v₉，第5阶段的状态为v₁₀，也是问题的结束。

状态的无后效性是指给定某一阶段状态后，决策过程由此阶段开始，以后的演变不受此阶段以前历史状态的影响。(www.daowen.com)

（3）决策（Decision） 从某一状态向下一状态过度时所做的选择。决策变量记为x_k，x_k是所在状态s_k的函数。

在状态s_k下，允许采取决策的全体称为决策允许集合，记为D_k（s_k）。各阶段所有决策组成的集合称为决策集。

策略（Strategy）从第1阶段开始到最后阶段全过程的决策构成的序列称为策略，第k阶段到最后阶段的决策序列称为子策略。

图6-2中，策略就是点v₁到v₁₀的一条路线，共有18个策略（18条路线）。最优策略是点v₁到v₁₀的最短路线。子策略可以是其他点到v₁₀的路线，显然策略也是子策略。

（4）状态转移方程（State transformation function） 某一状态以及该状态下的决策，与下一状态之间的函数关系，记为s_k+1=T（s_k，x_k）。

某一阶段的状态与下一阶段的状态有某种对应关系，是状态的转移规律，与所处状态及选择的决策有关。图6-2中，k+1阶段的状态等于k阶段某个状态下的决策。

（5）指标函数或收益函数（Return function） 是衡量对决策过程进行控制的效果的数量指标，具体可以是收益、成本、距离等指标。分为k阶段指标函数、k子过程指标函数及最优指标函数。

从k阶段状态s_k出发，选择决策x_k所产生的第k阶段指标，称为k阶段指标函数，记为v_k（s_k，xk）。从k阶段状态s_k出发，选择决策x_k，x_k+1，…，x_n所产生的第k阶段指标，称为k子过程指标函数，记为v_k（s_k，x_k，x_k+1，…，x_n）或V_k，n为阶段数。从k阶段状态s_k出发，对所有的子策略，最优的过程指标函数称为最优指标函数，记为f_k（s_k），通常取V_k的最大值或最小值。

在图6-2中，v_k（s_k，x_k）的含义是在状态s_k下选择决策x_k时的距离，如v₂（v₄，v₅）=13。V_k的含义是在状态s_k下选择某一条路线到v₁₀（决策序列）的距离，如v₂（v₃，v₆，v₈，v₁₀）=10+5+8=23。最优指标函数是某一点到v₁₀的最短距离。