【例5.8】 道路修建的成本控制问题。要修建一条L型的道路，总用地面积约为8528m²，材料费、人工费、机械使用费、其他的计划费用150000000元、30000000元、12000000元、8000000元，问如何来对使用成本进行控制。

备注：对于一个大型道路工程而言，优先因子P₁应赋予材料费，P₂赋予人工费，P₃赋予机械使用费，P₄为其他费用。

解 设x₁、x₂、x₃、x₄分别为每1m²实际耗用的材料费、人工费、机械使用费以及其他费用，为了进行成本控制，即使得成本最少，则有

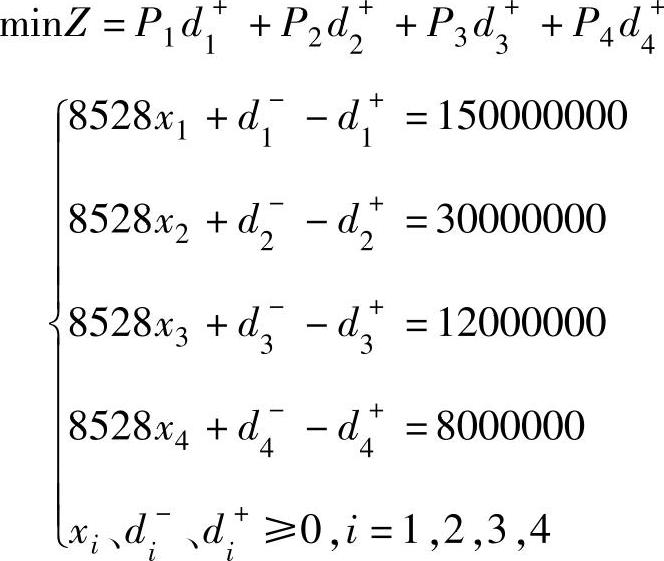
用目标规划求解该目标规划问题，得到满意解x₁=17589，x₂=3518，x₃=1407，x₄=938，即应将每平方米实际耗用的材料费、人工费、机械使用费以及其他费用控制为17389元、3518元、1407元以及938元，从而在施工过程中有效地控制了该工程的成本。

【例5.9】 公交调度问题。在公交调度问题中，考虑到乘客和公交公司的利益作如下规定：

1）公交公司追求的经济效益：平均满载率≥E（Z）。

2）公交的社会效益：乘客的等待抱怨程度≤E（W），乘客的拥挤抱怨程度≤E（C）。

3）公交公司现有车辆数及车辆完好率要求：所需总的车辆数≤E（V）。

4）公交公司现有行程和司乘人员安排的经济性要求：全天发车次数≤E（R）。(www.daowen.com)

假设全天的行车时间分为m段，每一段内发车时间间隔相同，每一段的发车次数分别为n₁，n₂，…，nm；此外，假设某路段站点数为b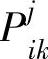，为第j时段内第i辆车经过第k站点后车上的人数，P_总为所有在车上的人数之和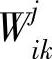；为第j时段内第i辆车经过第k站点时，在第k站等候时间超过忍耐时间的人数，W为平均等待抱怨程度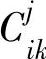；为第j时段内第i辆车离开第k站点时车上的超载人数，C为平均拥挤抱怨程度；ΔG_A（t）为t时刻不在A车场（上行起始站）的车辆总数。则有：

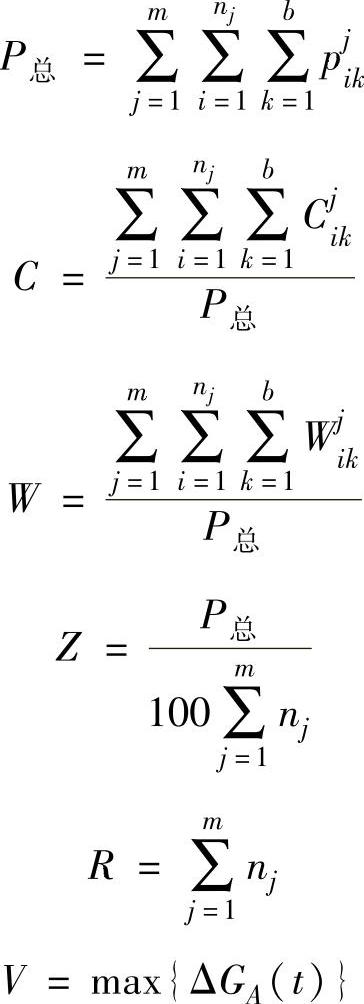
综上所述，建立公交调度的规划模型为：

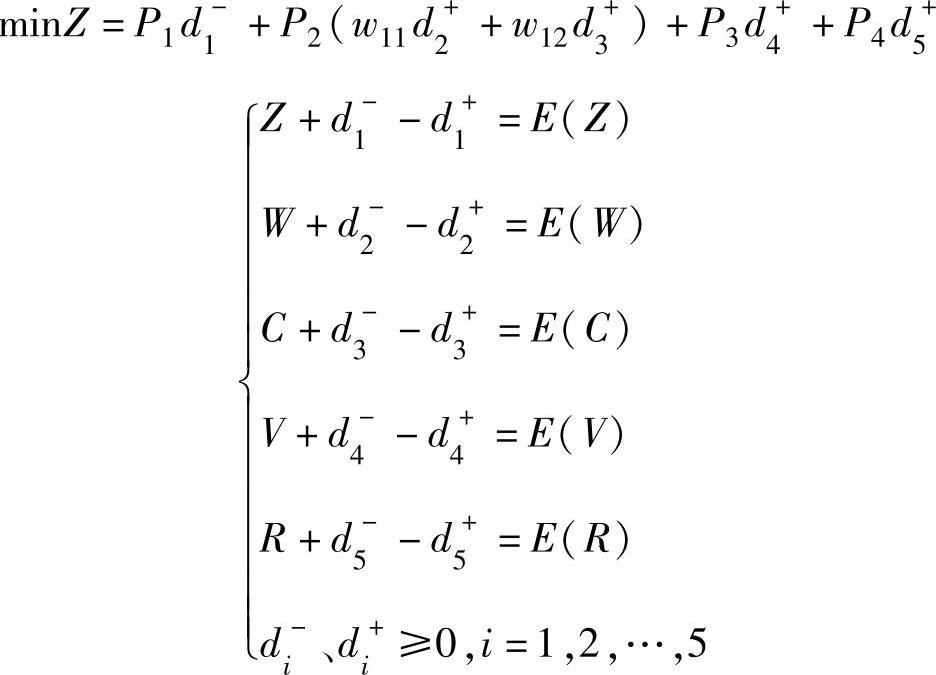
通过对某市27路车的跟踪调查，取得其到站时刻表以及在各站点上下车人数，用计算机编程，满载率E（Z）为83%，等待抱怨E（W）取4，拥挤抱怨E（C）取5%，车辆总数E（V）取10，全天发车次数E（R）为100次，w₁₁和w₁₂分别为7和3，最终求解结果见表5-10。

表5-10

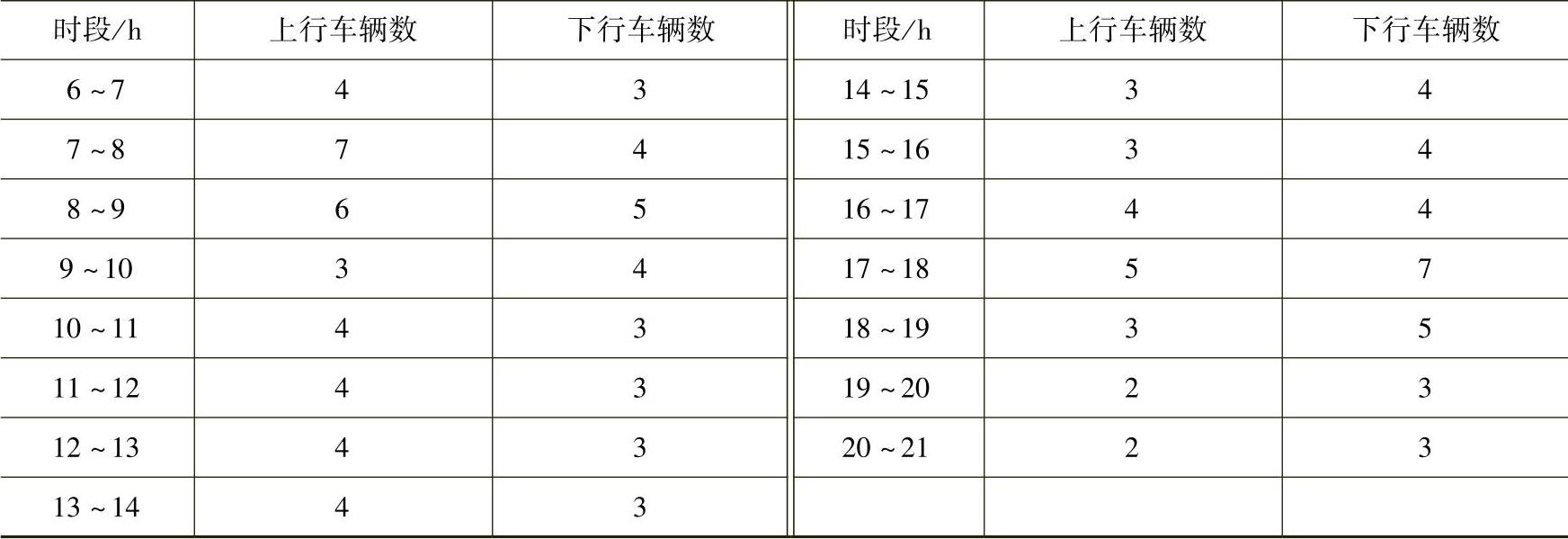
所需总的车辆数为13，总发车次数为116次。