对于只具有两个决策变量（不包含偏差变量）的目标规划的数学模型，可以用图解法来分析求解。

【例5.3】 用图解法求解下面的目标规划问题。

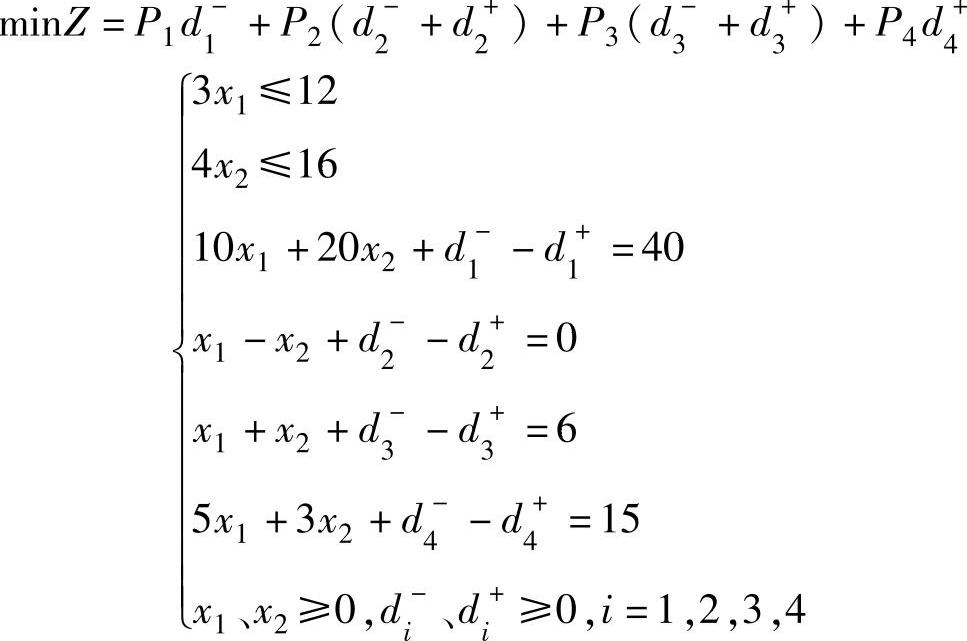
解 第一步，画出平面直角坐标系。系统约束的作图与线性规划相同，本例中满足前两个系统约束的可行域为矩形，如图5-1所示。

第二步，进行目标约束时，先令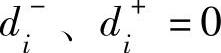，作相应的直线，然后标明偏差变量大于零时点（x₁，x₂）所在的区域。例如第三个约束中，当（x₁，x₂）在该直线的右上方时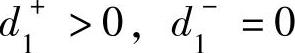；当（x₁，x₂）在该直线的左下方时。

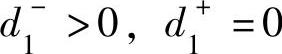第三步，根据目标函数中的优先因子来求函数的最小值。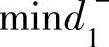的解在直线（3）的右上方；在直线（3）右上方的阴影部分中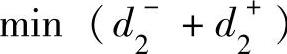的解在线段AB上；在线段AB上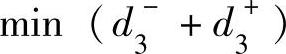的解是点C；满足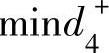的解得不到满足。因此点C（3，3）为目标规划的满意解。

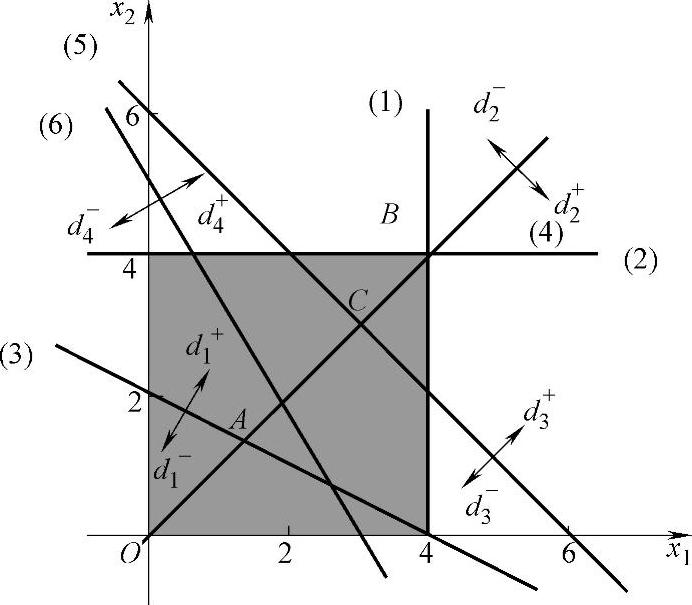
图5-1

【例5.4】 用图解法求解目标规划

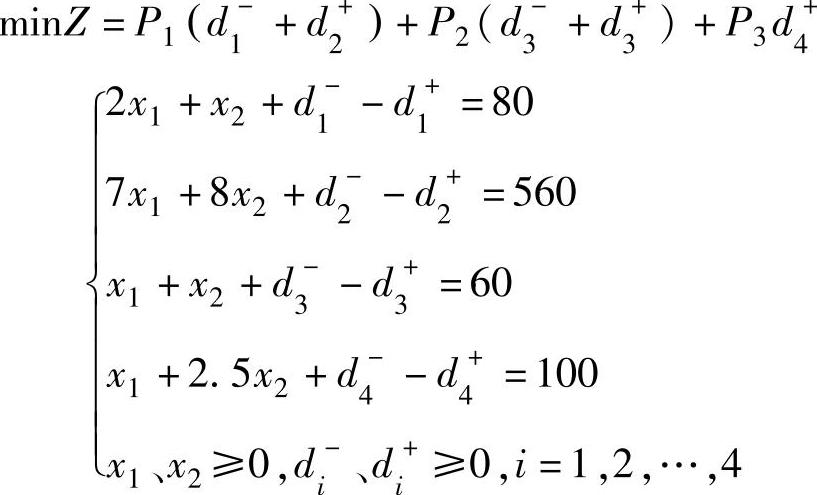(www.daowen.com)

解 先画出四个约束的直线，如图5-2所示。第一目标最小是图中的阴影部分；第二目标最小是图中的线段AC；第三目标最小是图中线段BC，即满意解为线段BC上任意点，端点的解是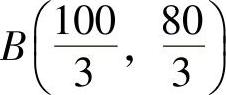，C（60，0）。

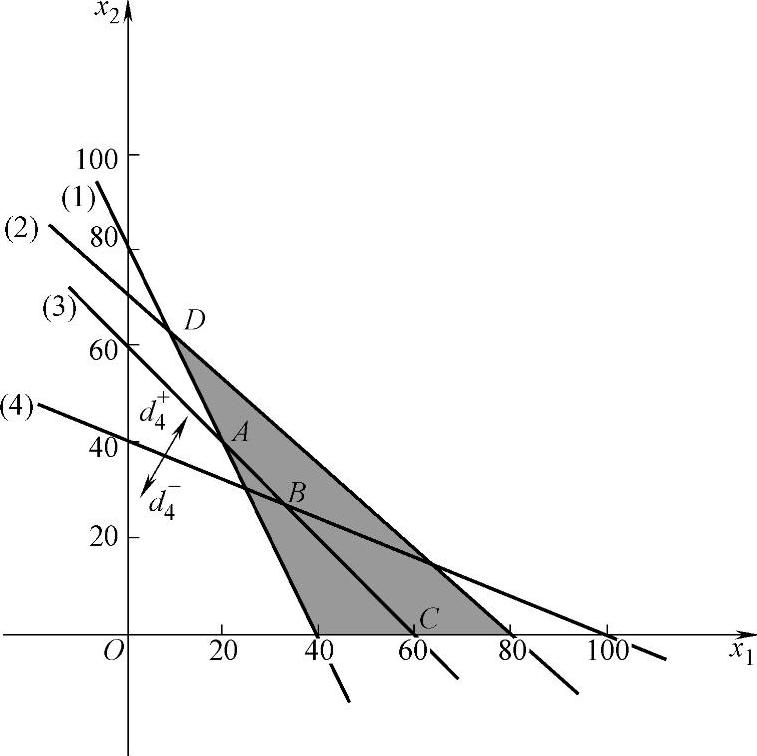
图5-2

如果目标函数变为：

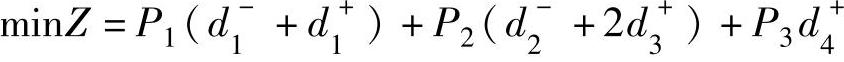
该目标函数可改写为：

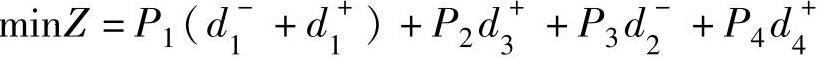
满意解为点D，不是点A。因此图解法求解时如果按权系数大小顺序求最小值很容易得到错误的解。