引入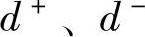分别为正、负偏差变量。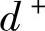表示决策值超过目标值的部分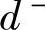；表示决策值未达到目标值的部分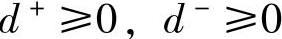，。因为决策值不可能既超过目标值同时又未达到目标值，所以。

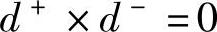一个规划问题常常有若干个目标。但决策者在要求达到这些目标时，是有主次的。要求第一位达到的目标赋予优先因子P₁，次位的目标依次赋予优先因子P₂，P₃，…，P_k，…，P_k+1，…，Pj。表示P_k比P_k+1有更大的优先权。

【例5.2】 求例5.1的目标规划模型。

解 首先按照决策要求，分别赋予这三个目标P₁、P₂、P₃优先因子。

1)设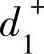为甲的产量超出乙的产量的部分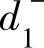，为甲的产量未达到乙产量的部分，于是有：

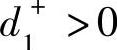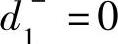甲的产量高于乙的产量时，且，则有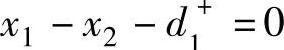

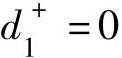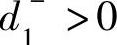甲的产量低于乙的产量时，且，则有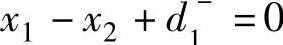

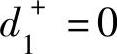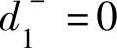甲的产量等于乙的产量时，且，则有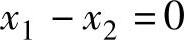

在实际中，上述三种情形只能发生一种，因而可将三个等式写成一个等式：

要使甲的产量不大于乙的产量，所以目标函数中甲的产量超出乙的产量的部分di+要尽可能小，即：

2）设为超过和未达到设备台时的偏差变量，则有：

3）同理设为超过和未达到56元利润的偏差变量，则有：(www.daowen.com)

4）需要注意的是还有一个变量要求为原材料不能超过现有量，不能有正负偏差，即：

2x₁+x₂≤11

这种要求结果一定不能有正的或负的偏差的约束称为系统约束，前面的带有正负偏差的约束称为目标约束。

综上所述，该问题的目标规划数学模型为：

应当注意的是决策者对于具有相同重要性的目标可以赋予相同的优先因子，若要区别具有相同优先因子的两个目标，可分别赋予它们不同的权系数w_j，如m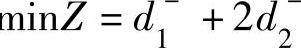等价于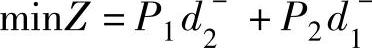。而权系数的确定方法有两两比较法、专家评分法等，依据权系数的大小区分它们的重要性，权系数越大越重要。

对于目标规划的目标函数，通常是按决策者的意愿事先给定所要达到的目标值，当期望值不超过目标值时，目标函数为：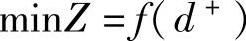

当期望值超过目标值时，目标函数为：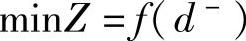

当期望值等于目标值时，目标函数为：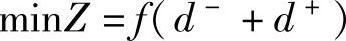

综上所述，目标规划的一般模型为：

式中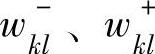，分别为第l个目标约束的正负偏差变量的权系数；g_l为目标的期望值。第一个约束为系统约束，第二个约束为目标约束。