【例4.15】 道路运输的最小费用问题。现有A₁、A₂、A₃三个道路桥梁公司，可供应砂分别为20t、20t和40t。现将砂运往B₁、B₂、B₃和B₄四个地区，需求量分别为30t、25t、10t和15t。已知运价如表4-25所示，试求使总运输费用最小的运输方案。

表4-25

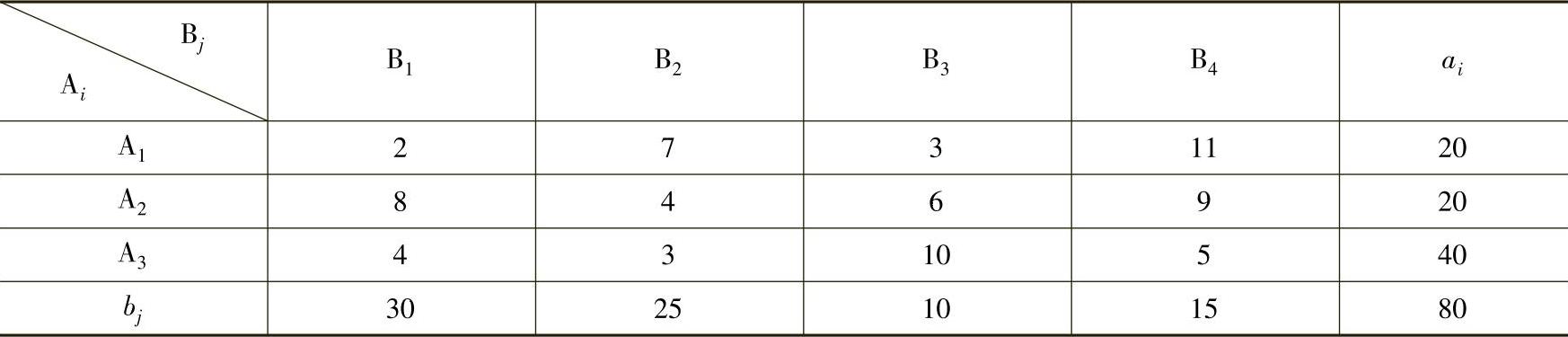
解 用最小元素法求得初始基本可行解见表4-26。

表4-26

用闭回路法求非基变量的检验数为：

λ₁₂=7-3+4-2=6

λ₁₃=3-6+9-5+4-2=3

λ₁₄=11-5+4-2=8

λ₂₁=8-4+5-9=0

λ₂₂=4-3+5-9=-3

λ₃₃=10-5+9-6=8

因为λ₂₂=-3＜0且为最小者，故选x₂₂进基，调整运量。x₂₂的闭回路是{x₂₂，x₂₄，x₃₄，x₃₂}，标负号的变量是x₂₄和x₃₂，取最小运量：

θ=min{x₂₄，x₃₂}=min{10，25}=10

故x₂₄出基，x₂₂和x₃₄加上10，x₂₄和x₃₂减去10，并在x₂₄处打上“×”作为非基变量，其余变量的值不变，调整后的方案见表4-27。

表4-27

重新求所有非基变量的检验数得：

λ₁₂=6，λ₁₃=0，λ₁₄=8，λ₂₁=3，λ₂₄=3，λ₃₃=5所有检验数λ_ij≥0，所以得到最优解为：

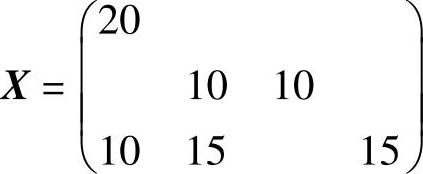
最小运费：

Z=2×20+4×10+6×10+4×10+3×15+5×15=300

由λ₁₃=0知，该问题具有多重最优解，求另一最优解的方法是令x₁₃进基，并在x₁₃的闭回路{x₁₃，x₂₃，x₂₂，x₃₂，x₃₁，x₁₁}上按上述方法调整运量，得到另一个最优解

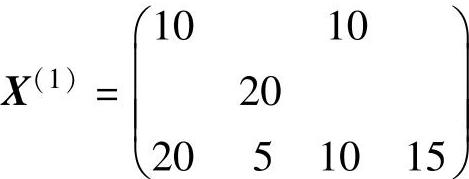
【例4.16】 交通分配问题。假设某交通分配问题有三个始点O_i（i=1，2，3）和四个终点D_j（j=1，2，3，4），始点O_i发生的出行交通量a_i、终点D_j吸引的出行交通量b_j及各始终点之间的出行时耗t_ij如表4-28所示，出行总量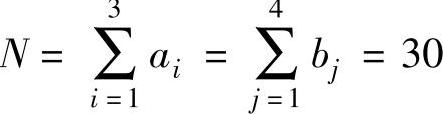。试求系统总时耗最小的出行量分配f_ij（i=1，2，3；j=1，2，3，4）。

表4-28

解 用最小元素法求得初始可行解，得到表4-29。(www.daowen.com)

表4-29

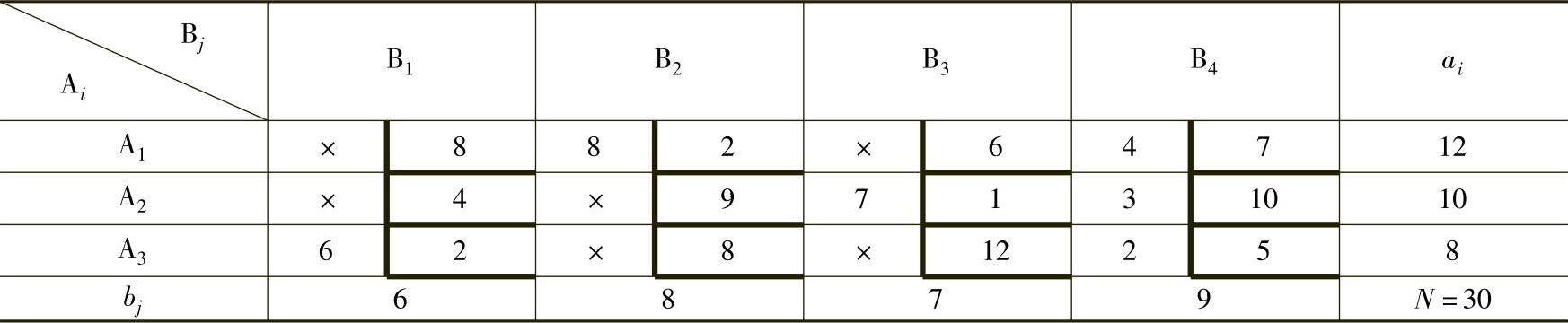
用闭回路法计算各非基变量的检验数为：

λ₁₁=4，λ₁₃=8，λ₂₁=-3，λ₂₂=4，λ₃₂=8，λ₃₃=15由于λ₂₁=-3＜0，所以要对上述问题进行调整，得到表4-30。

表4-30

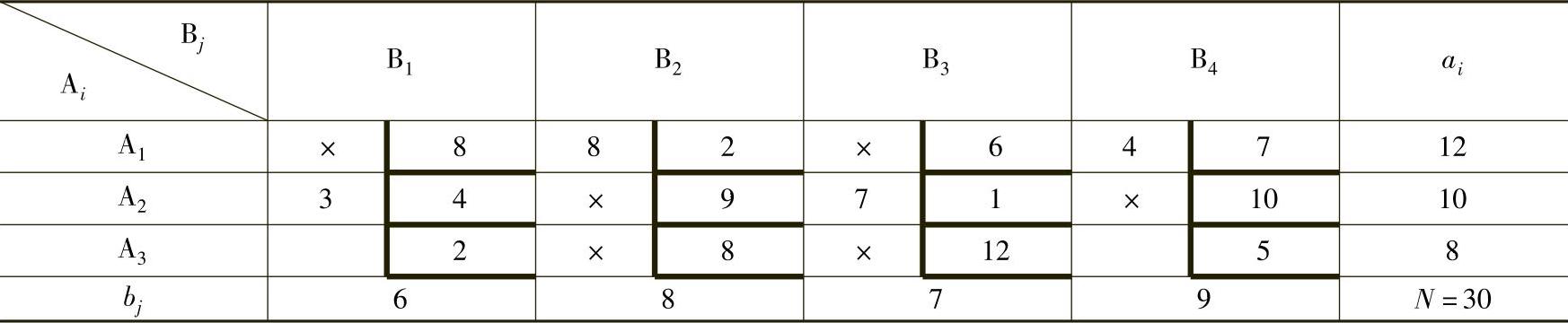
计算各非基变量的检验数为：

λ₁₁=4，λ₁₃=5，λ₂₂=7，λ₂₄=3，λ₃₂=8，λ₃₃=13

此时所有的检验数均大于零，说明表4-30给出的出行量分配f_ij是唯一最小的，即从O₁到D₂的出行量为8，到D₄的出行量是4；从O₂到D₁的出行量为3，到D₃为7；从O₃到D₁的出行量为3，到D₄为5，其余始点到终点的出行量均为0。相应的系统总时耗为：

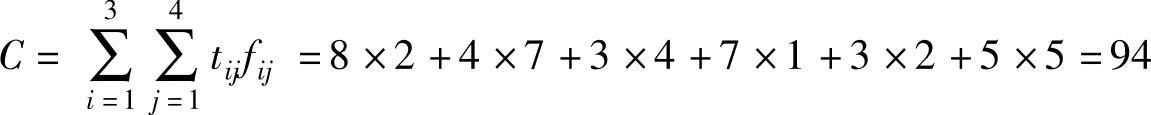
【例4.17】 公交车交接班问题。某公交公司在某一营运工作时段要安排5组司乘人员A_i（i=1，2，…，5）与5辆各路在线公交车B_j（j=1，2，…，5）的司乘人员进行交接班，每组司乘人员到各在线公交车辆交接班的时间为t_ij（i，j=1，2，…，5），见下面的矩阵（单位为min）：

解 设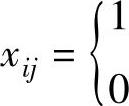：，若A_i组司乘人员被安排去交接B_j在线公交车辆时，i，j=1，2，…，5，否则

则使交接班总时间最少、最优交接班方案的数学规划模型如下：

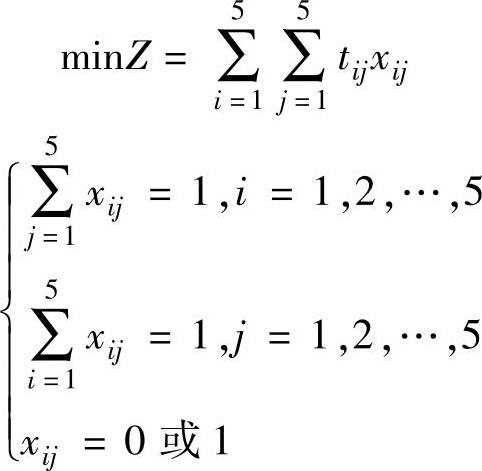
从效率矩阵的每行元素减去该行的最小元素得矩阵：

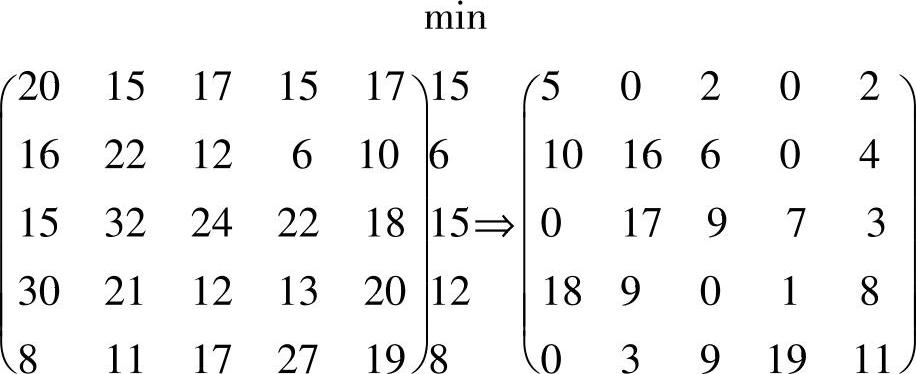
再将该矩阵的每列元素减去该列的最小元素得矩阵：

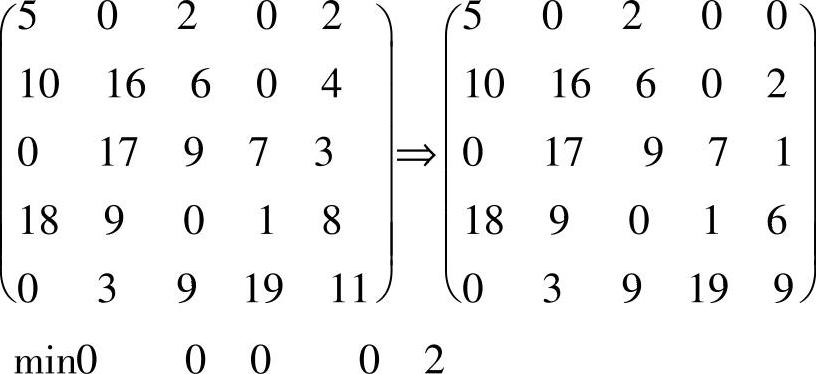
找出上述矩阵中的零元素，得到能够覆盖所有零元素的最少直线，结果如下：

此时，最多零元素的个数是4，不足5，在未被直线覆盖的元素中找到最小元素为1并且减去1，在直线相交处的元素加上1，再用最少直线数覆盖所有零元素得到矩阵：

相应的最优解为：

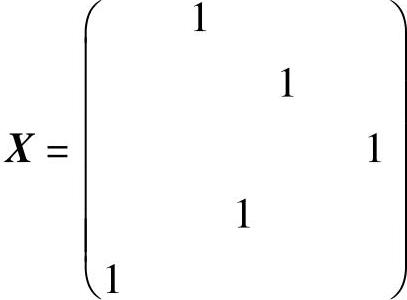
从上述最优解可知司乘人员交接班的最优匹配方案为：A₁组司乘员去交接B₂在线公交车辆，A₂组去交接B₄，A₃组去交接B₅，A₄组去交接B₃，A₅去交接B₁，此方案下各在线公交车辆所有交接班完成所需的总时间为：

T=15+6+18+12+8=59min