在实际应用中，常常会遇到求最大值、人数与任务数不相等以及不可接受的配置（某个人不能完成某项任务）等特殊指派问题，处理方法是将它们进行适当变换使其满足用匈牙利算法的条件，然后再求解。

指派问题求最大值的情况。设极大化问题的效率矩阵C=（c_ij），令矩阵B=（b_ij）=（M-c_ij）（通常令M等于效率矩阵C中的最大元素），则以B为系数矩阵的极小化指派问题和以C为系数矩阵的极大化指派问题有相同的最优解。

指派问题的人数和任务数不相等的情况。设分配问题中人数为m，任务数为n，当m＞n时虚拟m-n项任务，对应的效率为0；当m＜n时，虚拟n-m个人，对应的效率为0，将原问题化为人数与任务数相等的平衡问题再求解。

某人一定不能完成某项任务时，若原问题求最小值，令对应的效率为一个大M即可；若原问题求最大值，令对应的效率为0即可。

【例4.13】 某企业根据地域的需求计划在四个区域设立四个专业卖场，考虑的商品有电器、服装、食品、家具及计算机5个类别。通过市场调查，家具卖场不宜设在丙处，计算机卖场不宜设在丁处，不同商品投资到各点的年利润（万元）预测值见表4-22，该企业如何做出投资决策才能使年利润最大。

表4-22

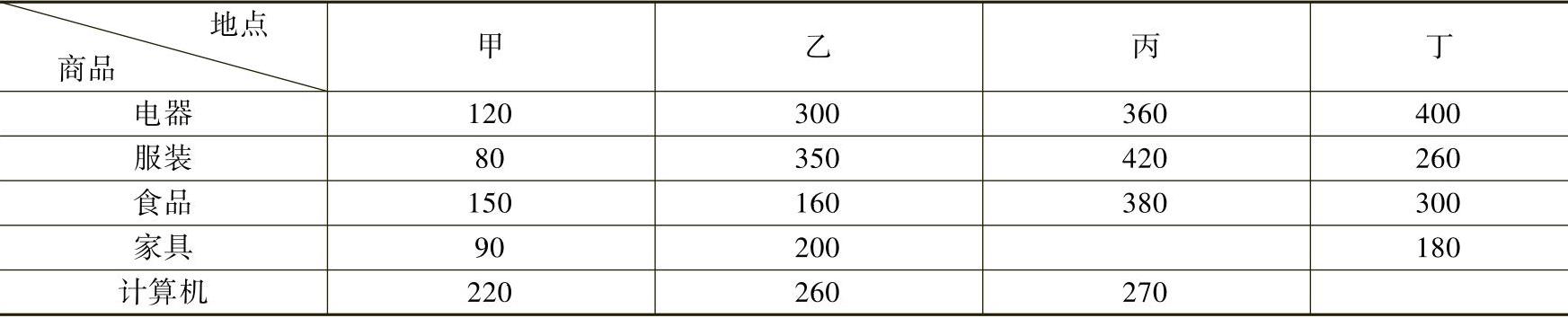
解 1）令c₄₃=c₅₄=0。

2）令M=420，转换成求最小值问题，得到效率表（机会损失表）。

3）虚拟一个地点戊，转换成平衡指派问题。

转换后得到表4-23。

表4-23

(www.daowen.com)

用匈牙利算法求得最优解为：

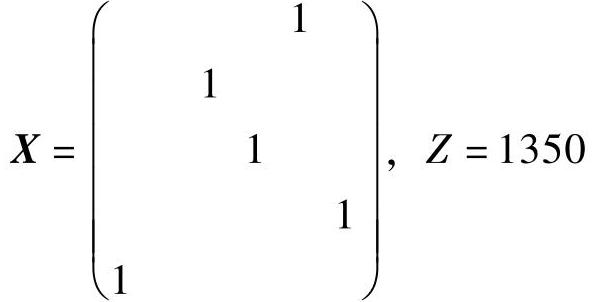
最优投资方案为地点甲投资计算机卖场，地点乙投资服装卖场，地点丙投资食品卖场，地点丁投资电器卖场，年利润总额预测值为1350万元。

【例4.14】 现有五个道路工程工地需要由三家砂石料公司供应所需的材料，已知每个公司到这五个工地的运输费用（百万元）如表4-24所示，求使总运费最小的指派方案。

表4-24

解 由于每家建筑公司最多可以承建两项，因此可把每家建筑公司看成两家建筑公司，其系数矩阵为：

上面系数矩阵有6行5列，为了使“人”和“事”数目相同，引入一个虚拟的项目己，使之成为标准指派问题的系数矩阵：

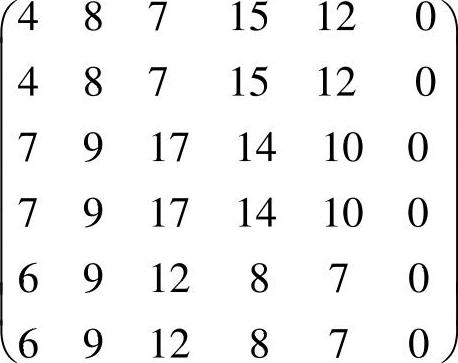
用匈牙利方法求解，得最小费用为：

Z=4+7+9+8+7=35（百万元）