匈牙利数学家克尼格（D.Konig）证明了定理4.4和定理4.5，基于这两个定理，解分配问题的计算方法被称为匈牙利算法。

匈牙利算法求指派问题的条件是：问题求最小值、人数和工作数相等以及效率非负。

【定理4.4】 如果从分配问题效率矩阵[c_ij]的每一行（列）元素中分别减去（或加上）一个常数u_i（v_j）得到一个新的效率矩阵[b_ij]，其中b _ij=c_ij-u _i-v_j，则[b _ij]的最优解等价于[c_ij]的最优解，其中c_ij及b_ij均非负。

【定理4.5】 若矩阵A的元素可分成“0”与非“0”两部分，则覆盖零元素的最少直线数等于位于不同行不同列的零元素（称为独立元素）的最大个数。

由定理4.5知，如果最少直线数等于m，则存在m个独立的零元素，令这些零元素对应的x_ij等于1，其余变量等于0，这时目标函数值等于零，得到最优解。

通过定理4.4，可将效率表中的某些元素转换为m个独立的零元素，通过定理4.5，可以判别出效率表中有多少个独立的零元素。

匈牙利方法求解指派问题的步骤为：

第一步：将效率矩阵[c_ij]每行的各元素减去该行的最小元素，再将所得矩阵每列的各元素减去该列的最小元素，那么所得矩阵的每一行和每一列都有零元素。

第二步：在第一步所得的矩阵中找出所有位于不同行不同列的零元素，并用最少条数的直线覆盖全部的零元素。画线及找独立的零元素的方法如下：

1）检查效率矩阵C的每行、每列，在零元素最少的行（列）中任选一个零元素并对其打上括号，将该“0”所在行、列其他零元素全部打上“×”，同时对打括号及“×”的零元素所在行或列画一条直线。

2）重复步骤1），在剩下的没有被直线覆盖的行、列中再找最少的零元素，打上括号、打上“×”及画线，直到所有的零元素被直线覆盖。如果效率矩阵每行（或列）都有一个打括号的零元素，则上述步骤得到的打括号的零元素都位于不同行不同列，令对应打括号零元素的变量x_ij等于1就得到了问题的最优解；如果效率矩阵中打括号的零元素个数小于m，转入第三步。

第三步：利用定理4.4对矩阵进行变换，增加独立零元素的个数。

【例4.12】 已知由A、B、C、D四项运输任务，现由甲、乙、丙、丁四个人负责完成，已知每个人完成每项运输任务的费用（百元）如表4-21所示，试求使总费用最小的指派方案。

表4-21

解 第一步：变换系数矩阵。(www.daowen.com)

找出效率矩阵中每行的最小元素，分别从每行中减去最小元素，得：

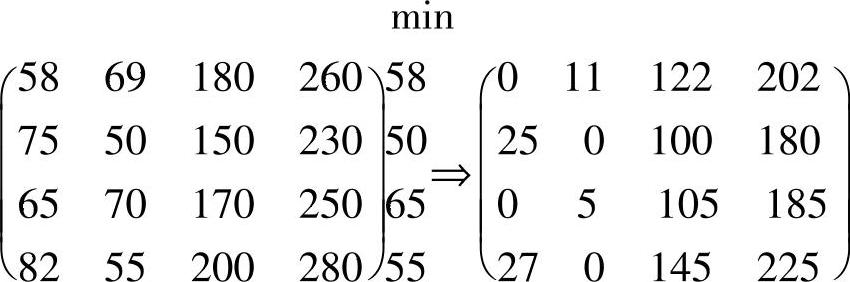
找出矩阵每列的最小元素，分别从每列中减去该最小元素，得：

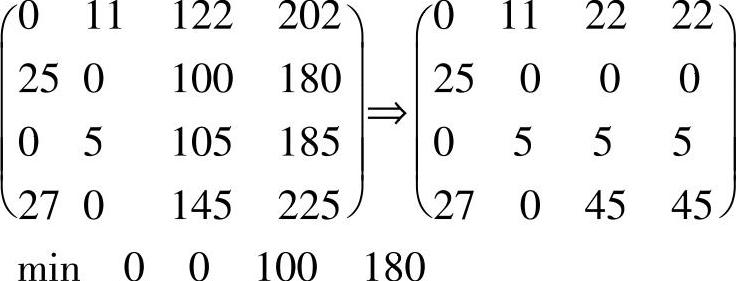
第二步：用最少的直线覆盖所有“0”得：

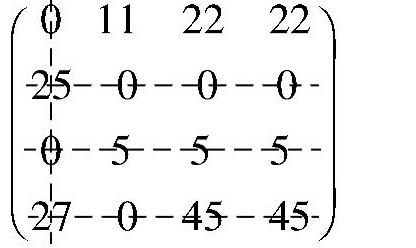
第三步：这里直线数等于3＜m=4，要进行下一轮计算。

1）从矩阵未被直线覆盖的数字中找出一个最小数k并且减去k，矩阵中k=5。

2）直线相交处的元素加上k，被直线覆盖而没有相交的元素不变。

3）回到第二步画线，最少直线数为4=m条，得到矩阵：

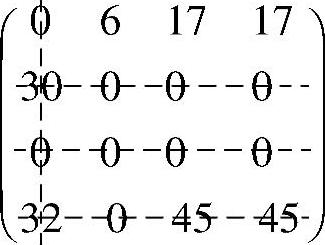
表明矩阵中存在4个不同行不同列的零元素，令这些零元素对应的变量x_ij等于1，其余变量等于0，得到两个最优解：

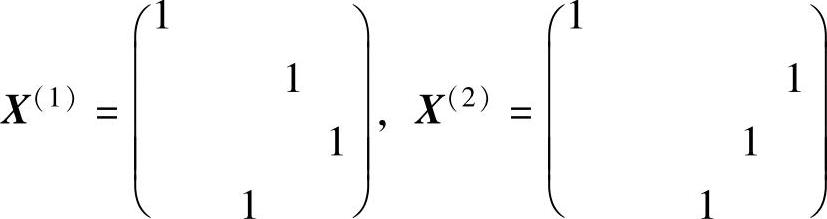
即最优方案有两个，第一种方案为甲完成任务A，乙完成任务C，丙完成任务D，丁完成任务B；第二种方案为甲完成任务A，乙完成任务D，丙完成任务C，丁完成任务B。最小费用为：

Z=58+150+250+55=513（百元）