在生活中经常遇到这样的问题，某单位需要完成n项任务，恰好有n个人可承担这些任务。由于每个人的专长不同，完成每项任务的效率也就不同。于是产生应指派哪个人去完成哪项任务，使完成n项任务的总效率最高的问题，这类问题称为指派问题或分派问题(As-signment Problem)。

在工程项目管理、资源利用和劳动力分配等实际工作中，指派问题比较常见。例如在工程运输中n个T程公司对n个T程项目的投标问题，公共交通客运公司运营的车辆与运营路线的分配问题等。

【例4.11】 设某运输队有4辆货车，需分派驶往4个不同的目的地，由于各辆货车的性能、消耗和效率不同，因而驶往各目的地的运输成本也不同，见表4-20（单位：百元）试求使总成本最低的车辆分派方案。

表4-20

解 此工作分配问题可以采用枚举法求解，分配方法有4！=4×3×2×1=24种。由于分配方案是目的地数的阶乘，计算量会很大。考虑到上述情况，可用0-1规划模型描述该问题。设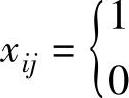：，若分配第i号车辆驶往第j个目的地，否则

则目标函数为：

minZ=37x₁₁+43x₁₂+33x₁₃+29x₁₄+

33x₂₁+33x₂₂+29x₂₃+25x₂₄+

34x₃₁+42x₃₂+38x₃₃+30x₃₄+(www.daowen.com)

37x₄₁+35x₄₂+30x₄₃+29x₄₄

要求每人完成一项工作的约束条件为：

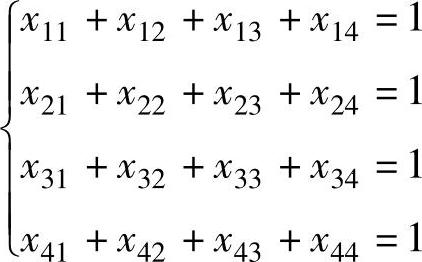
要求每项工作只能安排一个人的约束条件为：

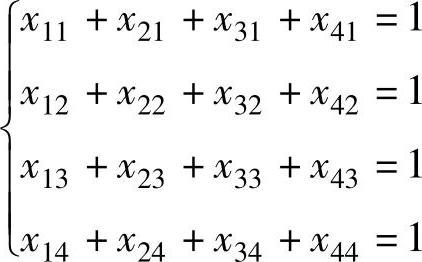
表4-20称为效率表，指派问题求最大值或最小值由效率表的含义确定。假设m个人恰好做m项工作，第i个人做第j项工作的效率为c_ij≥0，效率矩阵为[c_ij]，如何分配工作使效率最佳（min或max）的指派问题的数学模型为：

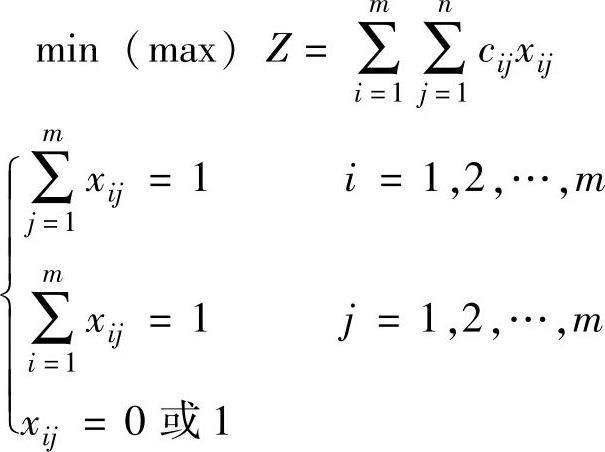
观察上述例题可知，指派问题既属于第3章的0-1规划模型，又是运输模型的特例。当然可用整数规划、0-1规划或运输问题的解法去求解，但这就如同用单纯形法求解运输问题一样不合算，利用指派问题的特点可有更简便的解法——匈牙利算法。