当某个检验数小于零时,需要调整运量从而改进运输方案,改进方法为闭回路法,其步骤为:
1)确定进基变量。选λlk=min{λijλij<0}对应的变量xlk进基。
2)确定出基变量。在进基变量xlk的闭回路中,将标有负号的最小运量θ对应的基变量为出基变量,并打上“×”以表示其为非基变量。
3)调整运量,在进基变量的闭回路中将标有负号的最小运量作为调整运量θ,标有正号的变量加上θ,标有负号的变量减去θ,其余变量不变,然后求新的基本可行解中非基变量的检验数,若全部检验数大于零,停止运算,若存在某个检验数λlk<0,则重复步骤1)和2)。
在确定出基变量时,当出现两个或两个以上最小运量θ,在其中任选一个作为非基变量,其他θ对应的变量仍为基变量,运量为零,得到退化基本可行解。在例4.3中求初始基本可行解时,如果同时划去一行一列,导致最后基变量个数少于m+n-1,此时需要在同时划去的一行一列对应打“×”的位置上标上一个“0”,此时也出现退化解。
注:运输单纯形法计算过程中,运量调整后必须将所有非基变量的检验数重新求一次。
【例4.7】 求下列运输问题的最小运输费用的最优解

解 用最小元素法求得初始基本可行解见表4-12。
表4-12

用闭回路法求非基变量的检验数为:
λ11=5-3+4-14+12-8=-4
λ13=9-8+12-14=-1
λ22=6-12+14-4=4
λ24=7-4+14-12+8-2=11
λ31=10-14+4-3=-3
λ34=5-2+8-12=-1
因为有4个检验数小于零,所以这组基本可行解不是最优解。λ11=min{λ11,λ13,λ31,λ34}=-4最小,故选x11进基,调整运量。x11的闭回路是{x11,x12,x32,x33,x23,x21},标负号的变量是x12、x33、x21,取最小运量:(www.daowen.com)
θ=min{x12,x33,x21}=min{40,15,45}=15
x33最小,故x33出基,调整量θ=15,在x11的闭回路上x11、x32、x23分别加上15,x12、x33、x21分别减去15,并且在x33处打上记号“×”作为非基变量,其余变量的值不变,调整后得到一组新的基本可行解,如表4-13所示。
表4-13

重新求所有非基变量的检验数得:
λ13=3,λ22=0,λ24=7,λ31=1,λ33=4,λ34=-1
λ34=-1<0,说明还没有得到最优解,x34进基,在x34的闭回路中,标负号的变量x14和x32,调整量为:
θ=min{x14,x32}=min{30,40}=30
x14出基。x12,x34分别加上30,x14和x32减去30,其余变量不变,得到一组新的基本可行解,如表4-14所示。
表4-14

求所有非基变量的检验数得:
λ13=3,λ14=1,λ22=0,λ24=8,λ31=1,λ33=4所有检验数λij≥0,所以得到最优解为:
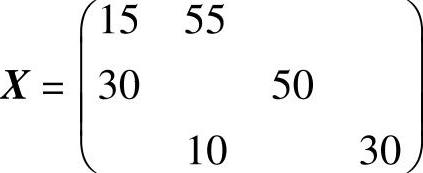
最小运费:
Z=5×15+8×55+3×30+4×50+12×10+5×30=1075
由λ22=0知,该问题具有多重最优解,求另一个最优解的方法是在x22的闭回路{x22,x21,x11,x12}上任意调整(保持可行),目标值不变,但只能得到一个基本最优解,其他都不是基本最优解,例如x22=5调整后得到最优解
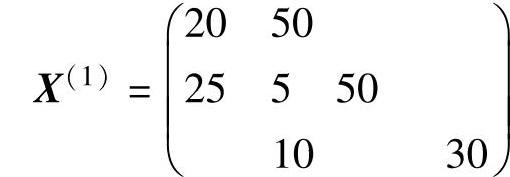
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






