判断初始运输方案是否为最优方案，仍然是用检验数来判别。因运输问题的目标函数都是求最小值，所以当所有检验数λ_ij≥0时，运输方案最优，否则，再改进当前的运输方案。下面介绍求检验数的两种方法：闭回路法和位势法。

1.闭回路法

这种方法求非基变量检验数的步骤为：

1）在基本可行解矩阵中，以该非基变量为起点，以基变量为其他顶点，找一条闭回路。

2）由起点开始，分别在顶点上交替标上代数符号+、-、+、-、…-。

3）用代数符号乘以相应的运价，代数和即为检验数。

【例4.5】 求下列运输问题的一个初始基本可行解及其检验数。矩阵中的元素为运价，右边的元素为产量，下方的元素为销量。

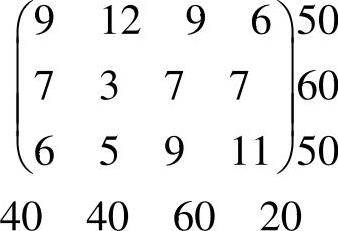
解 用最小元素法得到下列一组基本可行解为：

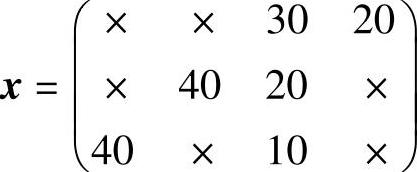
矩阵中打“×”的位置是非基变量，其余是基变量，这里只求非基变量的检验数。

求λ₁₁时，找出x₁₁的闭回路{x₁₁，x₃₁，x₃₃，x₁₃}对应的运价为{c₁₁，c₃₁，c₃₃，c₁₃}，将正负号交替标在各个运价处得到{+c₁₁，-c₃₁，+c₃₃，-c₁₃}，求和得到：

λ₁₁=9-6+9-9=3

同理可求出其他非基变量的检验数为：

λ₁₂=12-3+7-9=7

λ₂₁=7-6+9-7=3

λ₂₄=7-6+9-7=3

λ₃₂=5-9+7-3=0

λ₃₄=11-6+9-9=5

所有的λ_ij≥0（i=1，2，3；j=1，2，3，4），说明这组基本可行解是最优解。由于λ₃₂=0，由第1章可知该问题具有多重最优解。

下面介绍一下检验数的经济含义。假设给出初始基本可行解的表4-5中的x₁₁不是非基变量，将x₁₁增加一个单位变为x₁₁=1，为了保持产销平衡，应该使x₁₃减少一个单位，x₂₃增加一个单位，x₂₁减少一个单位，即构成了以非基变量x₁₁为起点，基变量x₁₃、x₂₃、x₂₁为其他顶点的闭回路。总运费的变化量ΔZ=3-3+2-1-1=λ₁₁，所以λ₁₁的含义就是当x₁₁增加一个单位后总运费的变化量ΔZ。

由检验数的经济含义可知，当所有非基变量的检验数都大于零时，说明不能增加任何非基变量的值，即不能将非基变量换入基变量，否则总费用增加，这时的基本可行解就是最优解；当某个非基变量的检验数λ_lk<0时，说明可以增加x_lk的值使总运费下降，这时的基本可行解不是最优解，需要对运输方案进行调整。

只要求得的基变量是正确的，且为m+n-1个，则某个非基变量的闭回路存在且唯一，相应的检验数也就唯一。(www.daowen.com)

2.位势法

闭回路法计算各个空格检验数时需要找出对应的闭回路，这使得在运输问题比较大时计算量很大。下面介绍较为简便的方法——位势法。

位势法求检验数是根据对偶理论推导出来的，设平衡运输问题为：

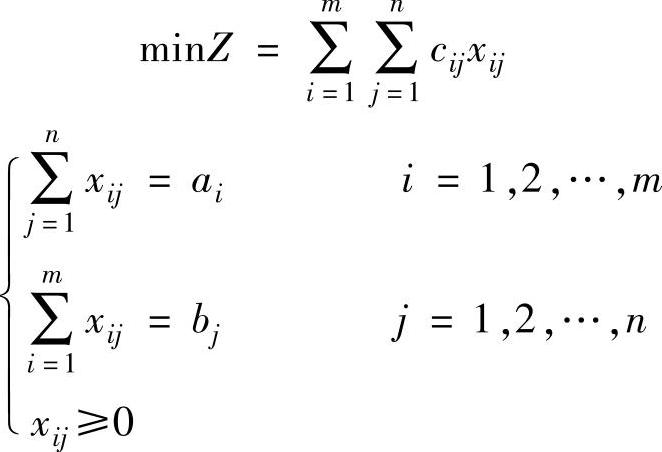
设前m个约束对应的对偶变量为u_i（i=1，2，…，m），后n个约束对应的对偶变量为v_j（j=1，2，…，n），则对偶问题为：

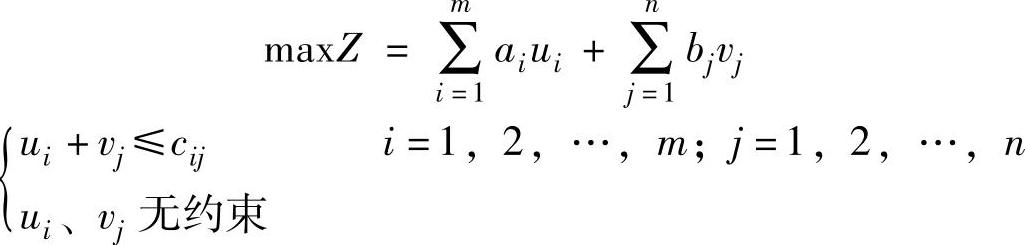
加入松弛变量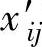将约束变换为等式：

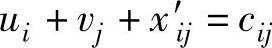
令原问题基变量X_B的下标集合为B，原问题x_ij的检验数是对偶问题的松弛变量x_i′_j，所以有：

由于基变量的检验数为0，所以有：

一般令u₁=0，先利用式（4-3）求得u_i和v_j的一组解，再利用式（4-2）求得非基变量的检验数。u_i和v_j为运输问题关于基变量组{x_ij}的对偶解，或称位势（u_i为行位势，v_j为列位势）。不同基变量组{x_ij}的取值不同，得到不同的位势，u_i和v_j具有无穷多组解，但对同一组基变量来说，所得的检验数是唯一的并与闭回路法求得的检验数相同。

【例4.6】 用位势法求例4.5给出的初始基本可行解的检验数。

解 求位势u₁、u₂、u₃及v₁、v₂、v₃、v₄，其中c_ij是基变量对应的运价，基变量共有6个，因此有6个等式方程：

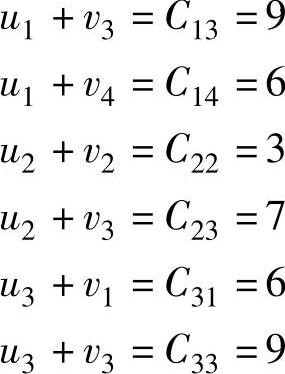
令u₁=0，得到位势的解为：

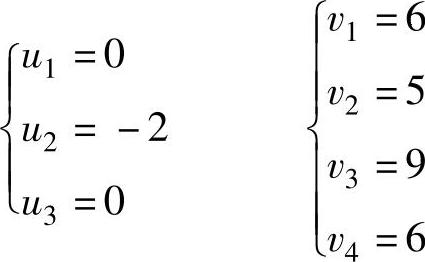
由公式λ_ij=c_ij-（u_i+v_j）求出非基变量的检验数为：

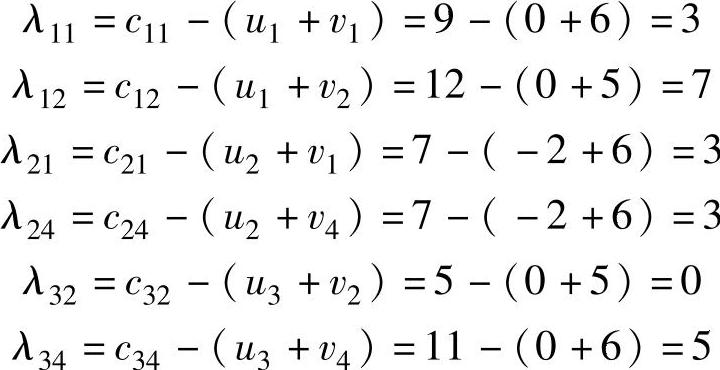
计算结果与例4.5相同。