与一般线性规划问题不同,任何运输问题都有基本可行解,也有最优解,根据具体情况,可能有唯一最优解也可能有多重最优解,如果供应量和需求量都是整数,则一定可以得到整数最优解。下面介绍几种常用的确定初始基本可行解的方法。
1.最小元素法
这种方法的基本思想是就近优先供应,即对单位运价表中最小运价cij对应的变量xij优先赋值xij=min{ai,bj},然后对次小运价对应的变量赋值并满足约束,依次下去,直到最后得到一个初始基本可行解。
【例4.2】 某建筑公司拟从A1、A2、A3三个管桩厂购买管桩,供应B1、B2、B3、B4四个工地使用。已知各管桩厂可供应管桩的数量(百根)、各工地需要的数量(百根)及从各管桩厂到各工地的运输单价(千元/百根)如表4-2所示,试用最小元素法求解该运输问题。
表4-2

解 表4-2中最小元素是c21=1,令x21=min{a2,b1}=min{4,3}=3,将3填在c21的下方,并在x11和x31的位置分别打上“×”,表示A2供应3个单位给B1,且B1已经满足需求,如表4-3所示。
表4-3

在表4-3没有分配的元素中,最小元素是c23=2,令x23=min{4-3,5}=1,将1填在c23的下方,在x22、x24处打上“×”,表示A2供应1个单位给B3,且A2已经没有剩余量,B3还差4个单位没有达到需求量,如表4-4所示。
表4-4

按照上述步骤依次进行下去,结果见表4-5。表4-5

表4-5中除了打“×”的变量共有m+n-1=3+4-1=6个,且不构成闭回路,因此{x13,x14,x21,x23,x32,x34}是一组基变量,打“×”的变量是非基变量。得到一组基本可行解为:
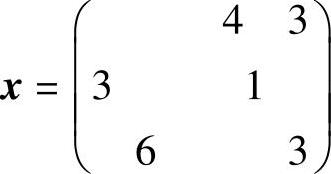
则目标值:
Z=3×4+10×3+1×3+2×1+4×6+5×3=86
2.元素差额法(Vogel近似法)
最小元素法的缺点是:可能开始时节省一处的费用,但随后在其他处要多花几倍的运费。元素差额法对最小元素法进行了改进。如果不能按最小运费就近供应,就考虑次小运费,这就有一个差额,差额越大,说明不能按最小运费调运时,运费增加就越多,因此对差额最大处就应当采用最小运费调运。基于此,元素差额法的步骤是:
1)求出每行和每列次小运价和最小运价之差,分别记为ui(i=1,2,…,m)和vj(j=1,2,…,n)。
2)找出所有行或列差额的最大值L=max{ui,vj},并且安排差额L对应行或列的最小运价处优先调运。
3)在剩下的运价中重复进行步骤1)和2),直到最后全部调运完毕。
【例4.3】 某市区交通愿望图有三个始点和四个终点,始点发生的出行交通量ai、终点吸引的交通量bj及始终点之间的旅行费用如表4-6所示。问如何安排出行交通量才能使总的旅行费用最小。
表4-6

解 求行差额ui=(3,1,2),求列差额vj=(4,1,7,4),则max{ui,vj}=max{3,1,2;4,1,7,4}=7,即v3=7最大,第三列的最小运价c23=2,先调运。令x32=min{a2,b3}=min{25,5}=5,在x13及x33处打“×”,结果如表4-7所示。(www.daowen.com)
表4-7
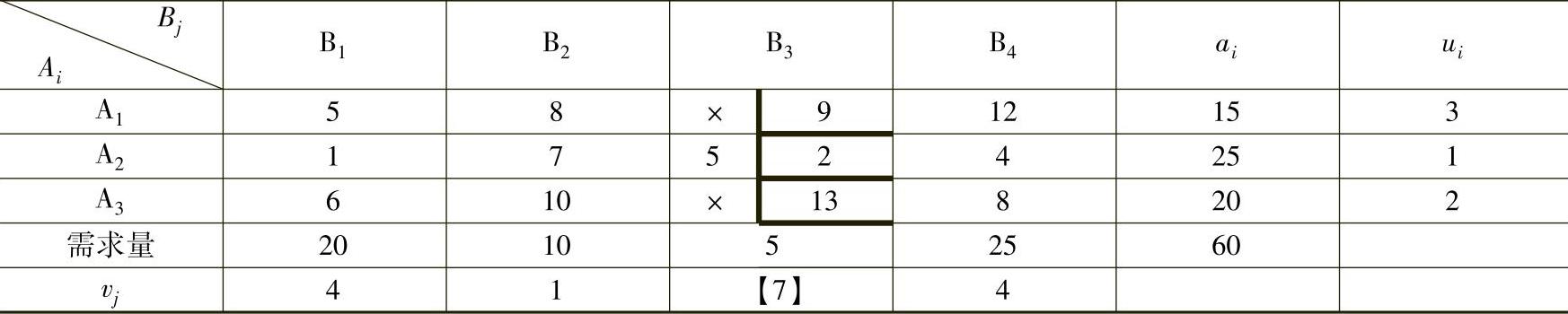
在表4-7中,因为B3已经满足需求,所以只求u1、u2、u3以及v1、v2、v4即可。这时发现有两个最大差额,即v1、v4,任选一个,如选v1=4(若选择v4=4,初始解的结果会不同),第一列的最小运价c21=1,故x21=min{25-5,20}=20,这时A2与B1同时满足约束,若同时将x11、x31、x22及x24都打上“×”,最后基变量的个数必定小于3+4-1=6个,因而应在x11、x31、x22及x24中任选一个变量作为基变量,运量为零,这里选x11=0,计算结果见表4-8。
表4-8

按照上述步骤依次进行下去,结果见表4-9。
表4-9

表4-9的基变量正好为m+n-1=3+4-1=6个且不包含闭回路,基本可行解为:
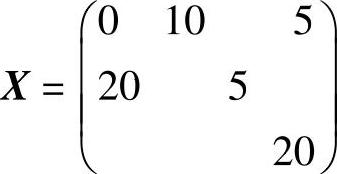
则目标值:
Z=8×10+12×5+1×20+2×5+8×20=330
3.左上角法(西北角法)
左上角法的基本思想是优先产销平衡表的左上角(西北角)的供应关系。即对单位运价表中左上角处的运价cij对应的变量xij优先赋值xij=min{ai,bj},当行或列分配完毕后,再对表中余下部分的左上角赋值,依次下去,直到右下角的元素分配完毕。
【例4.4】 试用西北角法求解例4.2的初始基本可行解。
解 左上角的元素是x11,则x11=min{7,3}=3且在x21、x31处打“×”,如表4-10所示。
表4-10

在表4-10余下第一、二、三行及第二、三、四列中,左上角的元素为x12,x12=min{7-3,6}=4,在x13、x14处打“×”。依次向右下角安排运量,结果如表4-11所示。
表4-11

表4-11给出的变量恰好是6个,且没有闭回路,基本可行解为:
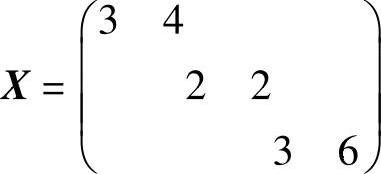
则目标值:
Z=3×3+11×4+9×2+2×2+10×3+5×6=135
从左上角法的基本思想可以看出,求运输问题的初始基本可行解的方法很多,如左下角、右上角、逐行(列)最小元素法等,只要得到的解满足约束条件,满足基变量个数是m+n-1且不包含闭回路就可得到一个基本可行解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






