在交通与物流工程中经常遇到运输问题这种特殊类型的线性规划模型，可以描述为某时期把某种产品从若干个产地调运到若干个销地。在已知各地生产量和需求量及各地之间运输费用的前提下，要求制定总运输费用最少的运输方案。运输问题属于特殊类型的线性规划，是线性规划在道路交通中应用的显著体现，下面以实例说明。

【例4.1】 现从两个产地A₁、A₂将物品运往B₁、B₂、B₃三个地区。各产地的产量、各需求地（销地）的需求量及产地到需求地的运价如表4-1所示，问如何安排运输计划使总的运输费用最小。

表4-1 运价表（单位：千元/t）

解 设x_ij（i=1，2；j=1，2，3）为第i个产地运往第j个需求地的运量，这样得到运输问题的数学模型为：

1）目标函数为总运费最小，即：

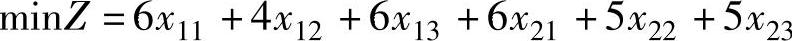
2）各产地的供给量与运出量应平衡，即：

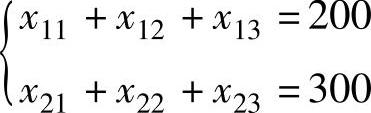
3）各需求地的供给量与需求量应平衡，即：

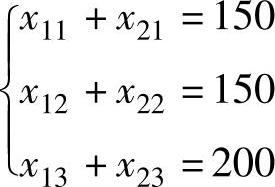
4）运量应大于或等于零，即：

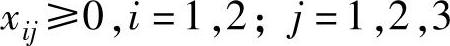
需要注意的是，有些问题表面上与运输问题没有多大关系，但其数学模型的结构与运输问题相同，我们把这类模型也称为运输模型。

已知有m个产地A_i，可供应某种物资，其供应量分别为a_i，i=1，2，…，m；有n个销地B_j，其需求量分别为b_j，j=1，2，…，n；从第i个产地到第j个销地的单位运费（运价）为c_ij；假设x_ij为在产销平衡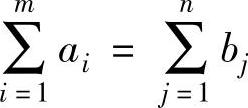的前提下第i个产地到第j个销地的运量，则使总运输费用最小的运输问题的数学模型为：

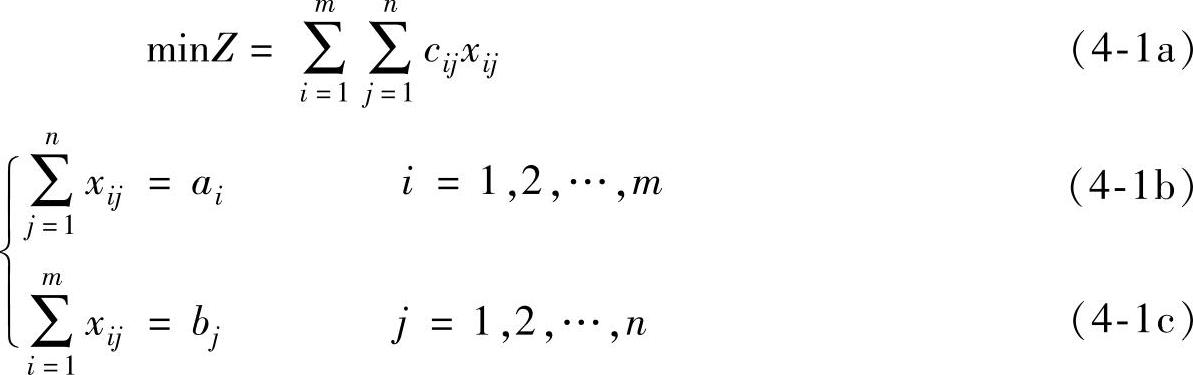
当目标是利润时，式（4-1a）改为求最大值；当总供应量大于总需求量时，式（4-1b）改为“≤”约束；当总供应量小于总需求量时，式（4-1c）改为“≤”约束。

通过上述线性规划模型可知，在供需平衡条件下，有m+n个等式约束和mn个变量，约束条件的系数矩阵A有m+n行、mn列。

为了在mn个变量中找出一组基变量，下面引用闭回路的概念。

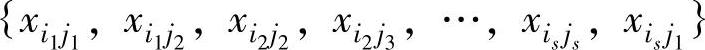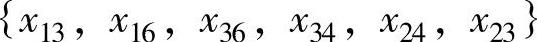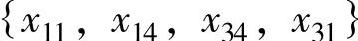称集合（i₁，i₂，…，i_s；j₁，j₂，…，j_s互不相同）为一个闭回路，集合中的变量称为闭回路的顶点，相邻两个变量的连线为闭回路的边，例如以及等都是闭回路。一条闭回路中的顶点数一定是偶数，回路遇到顶点必须转90°才能与另一个顶点连接。

若变量组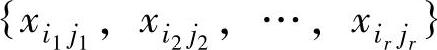中某一个变量是它所在行或列中出现的唯一变量，称这个变量是关于变量组的孤立点。很显然，若一个变量组不包含任何闭回路，则变量组必有孤立点；一条闭回路中一定没有孤立点；有孤立点的变量组中不一定没有闭回路。

由于运输问题的数学模型有它的独特性，所以它也有一些特殊的性质。(www.daowen.com)

【定理4.1】 设有m个产地n个销地且产销平衡的运输问题，则基变量数为m+n-1。

证 记系数矩阵A中x_ij对应的列向量为P_ij，由系数矩阵A的特征知第i个分量及第m+j个分量等于1，其余分量等于0，即：

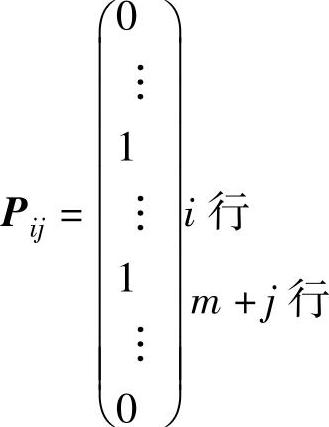
于是有：

将式（4-1b）的m个约束方程两边相加得：

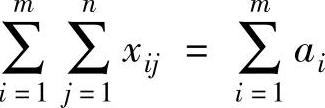
将式（4-1c）的n个约束方程两边相加得：

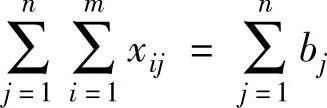
由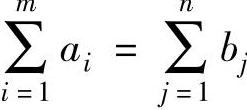知前m个约束方程之和等于后n个约束方程之和，m+n个约束方程是中任意m+n阶子式等于零，取第一行到m+n-1行与相关的，系数矩阵A中任意m+n阶子式等于零，取第一行到m+n-1行与x₁，n，x₂，n，…，x_m，n，x₁₁，x₁₂，…，x_1，n-1对应的列（共m+n^-1列）组成的m+n-1阶子式：

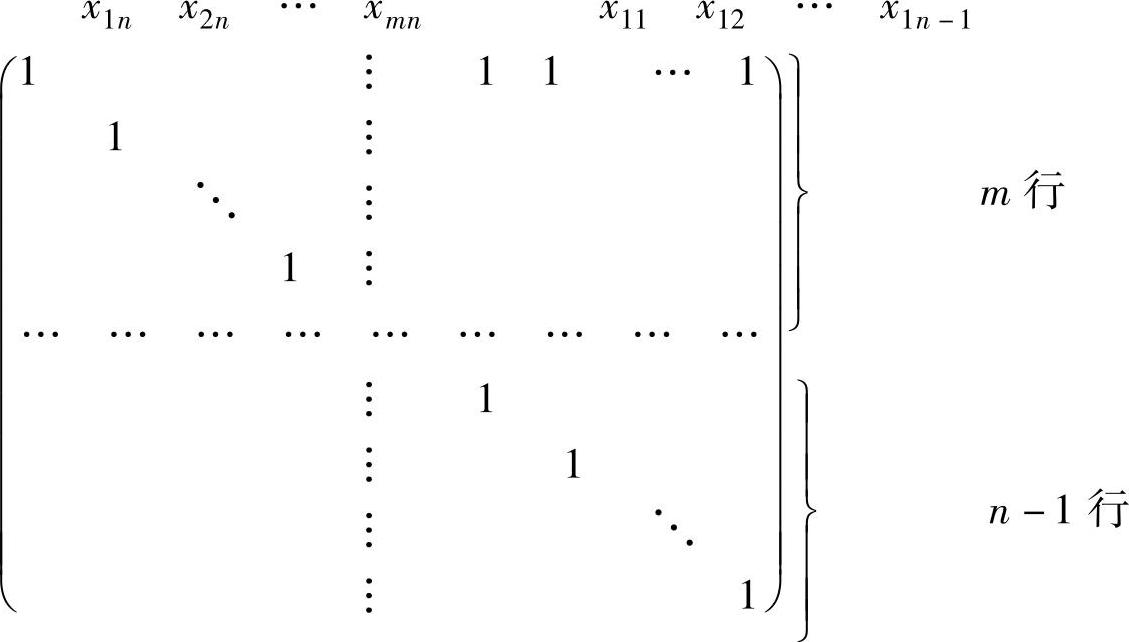
不等于零，故r（A）=m+n-1，所以产销平衡运输问题有m+n-1个基变量。

【定理4.2】 若变量组B包含有闭回路C={x_i1j1，x_i1j2，…，x_isj1}，则B中的变量对应的列向量线性相关。

证 将闭回路C中列向量分别乘以正负号线性组合后等于零，即：

P_i1j1-P_i1j2+P_i2j2-…-P_isj1=0

因而C中的列向量线性相关。由线性代数知，向量组中部分向量组线性相关，则该向量组线性相关，所以B中列向量线性相关。

由定理4.2可知，当一个变量组中不包含有闭回路，则这些变量对应的系数向量线性无关。因此对于运输问题，只要m+n-1个变量中不包含闭回路，就可找到一组基变量，从而得到定理4.3。

【定理4.3】 m+n-1个变量组构成基变量的充要条件是它不包含任何闭回路。

由定理4.3知，若要判断一组变量是否为基变量，只要看这组变量是否是m+n-1个，且是否构成闭回路。

由于运输问题具有以上特征，所以求解运输问题时，可用比较简单的计算方法——运输单纯形法求解。