0-1型整数规划是整数规划中的特殊情形，它的变量仅可取值0或1，这时的变量x_i称为0-1变量，或称为二进制变量。0-1型整数规划中0-1变量作为逻辑变量，常被用来表示系统是否处于某一特定状态，或者决策时是否取某个方案，即：

下面通过实例来认识一下0-1规划在实际道路交通问题中的应用。

【例3.7】 某道路修筑公司在同一时间内可参加A₁、A₂、A₃、A₄四项道路工程的投标。这些项目要求的工期相同。公司根据招标文件和本公司的技术水平对每项工程进行了仔细的研究和计算，将各项工程的预期利润、主要程序的工程量及本企业的施工能力列于表3-5。试建立使总利润最大的数学模型。

解 设

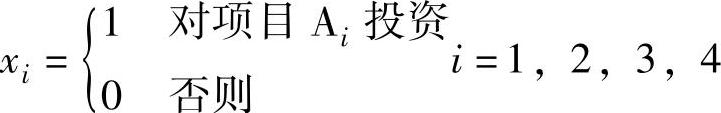
表3-5

则该问题可以描述成如下的线性规划

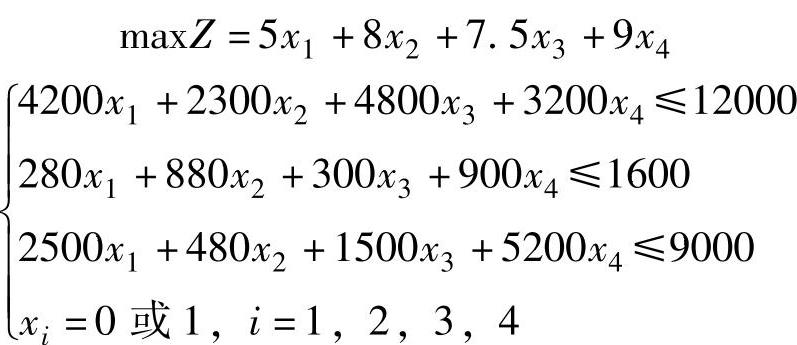
对0-1规划求解，将0-1规划的变量改为O≤x_j≤l并且为整数，就可以用分支定界法或割平面法求解。由于0-1规划的特殊性，用隐枚举法更为简便。其求解步骤如下：

1)寻找一个初始可行解xo，得到目标函数值的下界ZO，（最小值为题则为上界）。

2)列出2ⁿ个变量取值的组合，当组合解X_j对应的目标值Z_j小于ZO(max)时，认为不可行，当Z_j大于等于Zo(max)时，再检验是否满足约束条件，得到0-1规划的可行解。(www.daowen.com)

3)依据Z_j的值确定最优解。

这里的下界Zo可以动态移动，当某个Z_j大于Zo时，则将Z_j作为新的下界。

【例3.8】 用隐枚举法求解下列0-1规划问题：

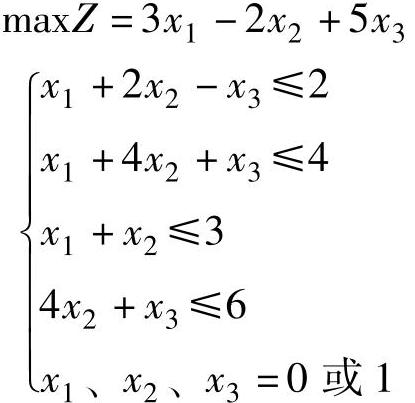
解 1）首先通过观察法找到一个初始可行解，例如X₀=（1，0，0）^T，则目标函数值Z₀=3为0-1规划问题的下界。

2）根据下界Z₀，构造一个新的约束条件3x₁-2x₂+5x₃≥3，增加到原来的约束条件中，并且把它放到第一个约束条件的位置，原0-1规划问题就可以写为：

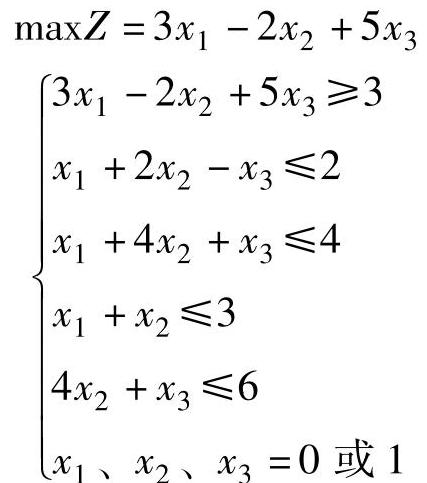
3）列出变量取0和1的组合共8个，依次检查各种变量组合是否满足新增加的约束条件，如果满足，则继续检查是否满足其他约束条件，如果约束条件都满足，则找到一个新的可行解，求出它的目标函数Z_j。继续检查其余变量组合，直到所有变量组合都被检查完毕，得到最优解。

如果变量组合不满足新增加的约束条件，则其后面的约束条件不需要再进行计算。

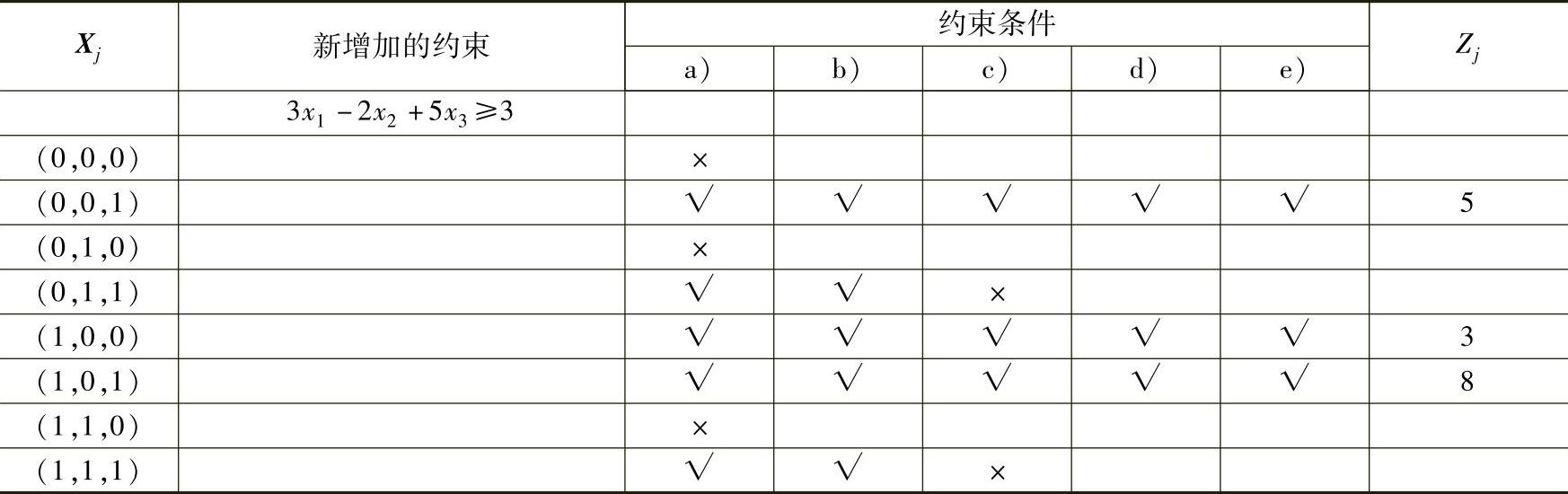
求解过程见表3-6，表3-6中a为新增加的约束条件，而表3-6b、c、d、e为原问题的约束条件，“×”代表不满足约束，“√”代表满足条件，空格代表不需要计算。由表3-6知0-1规划问题的最优解为X=（1，0，1）^T，最优值为Z=8。

表3-6