割平面法由高莫雷于1958年提出，其基本思路是先不考虑变量x_i为整数这一条件，对原问题求解，若得到非整数的最优解，则增加能割去非整数解的线性约束条件，使得由原可行域中切割掉一部分，切割掉的部分只包含非整数解。

将上述方法进行一般化描述：

1）设x_i是整数规划的松弛问题最优表上第i行约束方程所对应的基变量，其取值为非整数，x_j为非基变量，则其约束方程式为：

2）将a′_ij及b′_i拆分为一个整数和一个非负真分数之和，则得到：

式中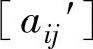、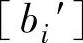分别为不超过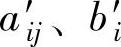的最大整数，而0≤f_ij<1，0≤f_i＜1。将（3-2）式代入（3-1）式可以得到：

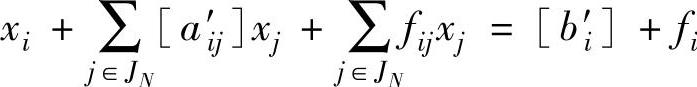
为大于等于零的整数，因此有：

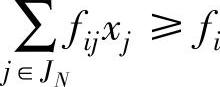
加入松弛变量x_s，变换为等式得到：

式（3-3）就是割平面方程的最基本形式，增加的新约束称为割平面方程或高莫雷约束方程。

【例3.6】 用割平面法解整数规划问题

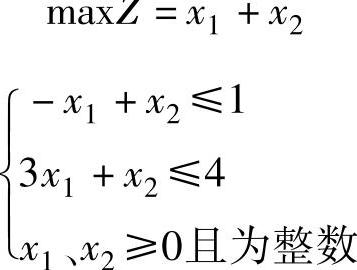
解 首先放宽约束变量，原问题对应的松弛问题为：

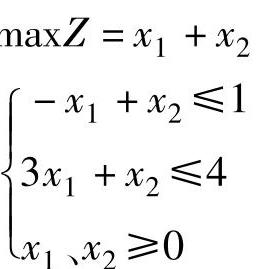
用单纯形法求解原问题的松弛问题，得到最优单纯形表，如表3-3所示。

表3-3

在松弛问题最优表上，任选一个含有不满足整数条件基变量的约束方程。这里选x₁，则含x₁的约束方程为：

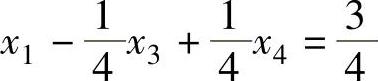
将所选的约束方程中非基变量的系数及常数均拆成一个整数加一个非负的真分数之和，则上式变为：(www.daowen.com)

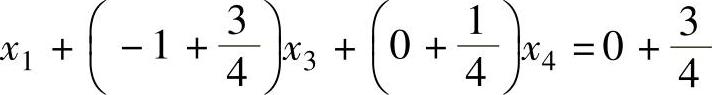
将上式中的非基变量系数及常数项中的非负真分数部分移到等号左端，将其他部分移到等式右端，得：

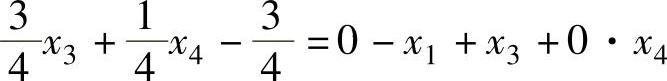
上式的等式右端由三部分组成：常数项的整数部分、基变量和非基变量（含松弛变量或剩余变量）。前两部分都是整数或应取整数，而松弛变量根据约束方程来看也应取非负整数（对于这一点，当原整数规划问题的约束方程组中的系数或常数项中有非整数时，要求将该约束方程先变换成整数系数及整数常数项，然后再标准化，就可满足），因此，上式右端应为整数，同时由于等式左端的特殊性，右端的整数应是大于等于零的整数。这时可将上式改写成：

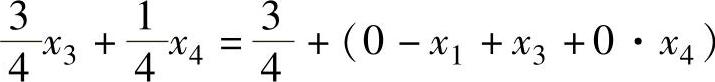
上式左端是非负数，右端第一项是一个真分数，如果第二项为负整数（即≤-1的整数），则不能保证左端为非负数。因此，左端应大于等于零：

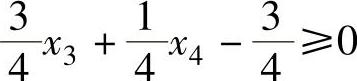
即

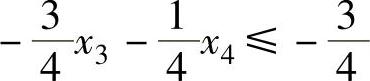
加入松弛变量x₅，得到高莫雷约束方程：

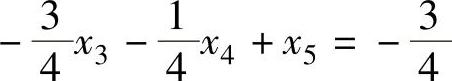
将高莫雷约束方程加到松弛问题的最优表中，用对偶单纯形法继续求解，如表3-4所示。

表3-4

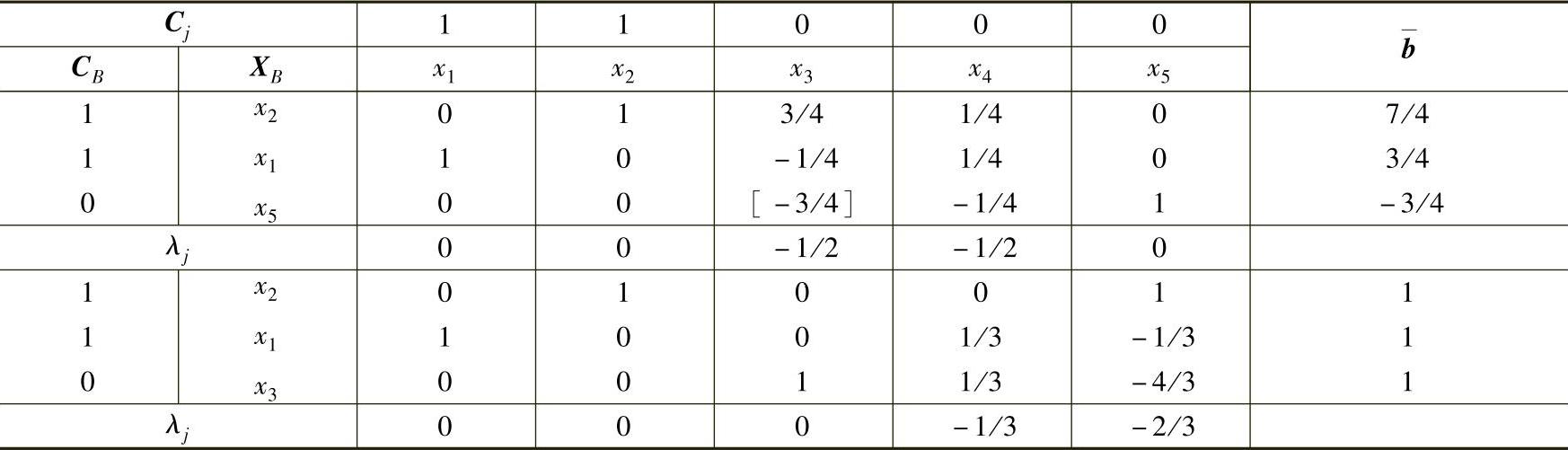
由最优表3-4可以看出，最优解为X=（1，1）^T，最优值为Z=2。

如果在增加了一个高莫雷约束方程的情况下，还没有得到整数最优解，则继续进行割平面，重复上述计算过程，直到得到整数最优解。

综上所述，割平面法的求解步骤为：

1）利用单纯形法求解整数规划的松弛问题。

2）若松弛问题不可行，则整数规划不可行；否则，设松弛问题的最优基为B，相应的最优解为X，转步骤3）。

3）若X为整数向量，则X为整数规划问题的最优解，停止运算；否则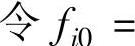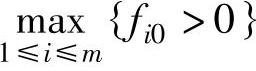，，以第i行为源行作割平面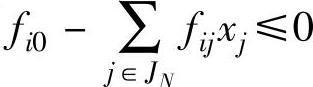，转步骤4）。

4）引入松弛变量x_s，将割平面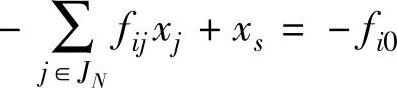添加到松弛问题的最优单纯形表中，继续利用对偶单纯形表法求解，转步骤2）。