整数规划相对于其松弛问题而言，二者之间既有联系，又有本质的区别，表现在以下几个方面：

1）整数规划问题的可行域是其松弛问题的一个子集。

2）整数规划问题的可行解一定是其松弛问题的可行解。

3）一般情况下，松弛问题的最优解不会刚好满足变量的整数约束条件，因而不是整数规划的可行解，更不是最优解。

4）对松弛问题的最优解中非整数变量简单地取整，所得到的解不一定是整数规划问题的最优解，甚至也不一定是整数规划问题的可行解。

【例3.5】 求解下述整数规划maxZ=40x₁+90x₂

解 1）先求解此整数规划松弛问题的最优解，其松弛问题为：

maxZ=40x₁+90x₂

用图解法得到其最优解为：

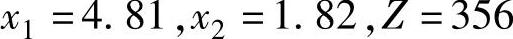
可见它不符合整数条件，这时Z是原问题的最优目标函数值Z^∗的上界，记作Z。而x₁=0、x₂=0显然是原问题的一个整数可行解，这时Z=0是Z∗的一个下界，记作Z，即0≤Z^∗≤356。

2）因为x₁、x₂当前均为非整数，可以任选一个变量进行分支。这里选x₁进行分支（也可以选x₂），于是对原问题增加两个约束条件：

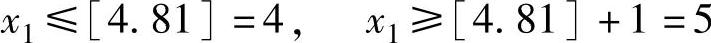
可将原问题的松弛问题分解为两个分支LP1和LP2。

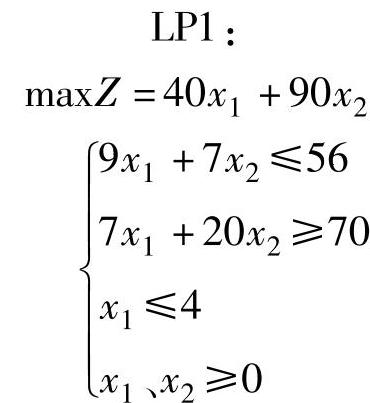
用图解法求解LP1和LP2，得到最优解为：(www.daowen.com)

3）显然没有得到全部变量是整数的解，继续对问题LP1和LP2进行分支，因Z₁>Z₂，故先分解LP1为两支，增加条件x₂≤2，称为LP3；增加条件x₂≥3，称为LP4。

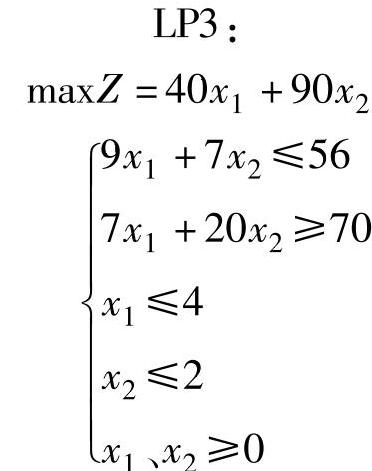
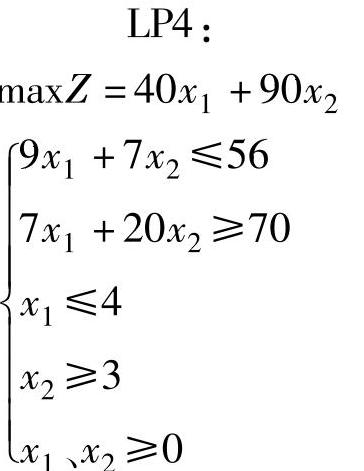
通过图解法求得LP3和LP4最优解为：

LP3的最优解已经都是整数，其目标函数值Z₃=340，大于Z₄=327。因此已经没有必要再分解LP4。由于LP2的Z₂=341，大于Z₃，Z^∗可能在340和341之间有整数解。因此对LP2进行分支，得到LP5和LP6。

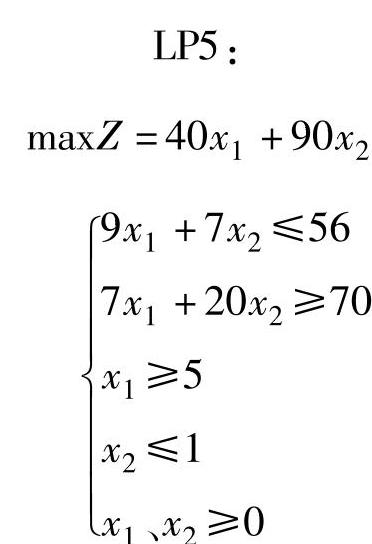
通过图解法求得LP5和LP6最优解为：

由于LP5存在非整数解x₁=5.44，并且Z₅=308，小于Z₃，已经无再分解的必要，而LP6为无可行解。于是有：

Z^∗=Z₃=340

LP3的解X₁=4.00，X₂=2.00为最优整数解。

上述分支过程可用图3-2表示。

图3-2