前两章讨论的一般线性规划问题，变量都是取实数值。但实际问题中，有些变量必须取整数值，例如公交规划中公交车辆的分配，建筑设备的合理分配等问题中，都要求其中的车辆数、机械设备数和产品件数为整数。这种要求部分或全部决策变量是整数的规划问题称为整数规划，简记IP。

整数线性规划问题可以分为以下几类：

1）纯整数线性规划：指全部决策变量都必须取整数值的整数线性规划。

2）混合整数线性规划：决策变量中有一部分必须取整数值，另一部分可以不取整数值的整数线性规划。

3）0-1型整数线性规划：指决策变量只能取值0或1的整数线性规划。

整数规划在道路交通问题的应用中极为广泛，下面以实例介绍。

【例3.1】 某公交车队决定，驾驶员每周连续工作5天后，连续休息2天，轮流休息。根据统计，车队每天需要的驾驶员人数如表3-1所示。车队的调度应如何安排每天上班的驾驶员人数，使车队总的驾驶员最少？

表3-1 所需驾驶员数统计表

解 设x_j（j=1，2，…，7）为休息两天后星期一到星期日开始上班的驾驶员数量，则这个问题的线性规划模型为：

【例3.2】 某桥梁工地为了制作桁架，需在长度为L米的角钢上截取长度分别为a₁，a₂，…，an米的单件，怎样截取才能使得角钢的残料最少。

解 设x_i为在长度为L米的角钢上截取a_i米单件的根数，i=1，2，…，n。z是截取后的残料长度，则问题就是求x_i（i=1，2，…，n）和z，这是一个混合整数线性规划，用数学式可表示为

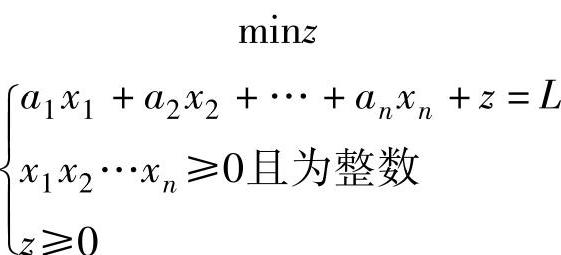(www.daowen.com)

【例3.3】 某厂拟用集装箱托运甲、乙两种货物，每箱的体积、重量、可获利润以及托运所受的限制如表3-2所示。问如何安排可使获得利润最大。

表3-2

解 设x₁、x₂分别为甲、乙两种货物的托运箱数。这是一个纯整数规划问题，用数学式可表示为

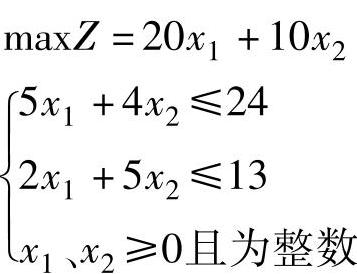
对于求解整数规划问题，为了满足整数解的要求，似乎对线性规划最优解“舍入化整”可以求得解，但这常常得不到可行解，即使得到可行解，也不一定是最优解，如例3.4所示。【例3.4】 求下列整数规划问题的最优解

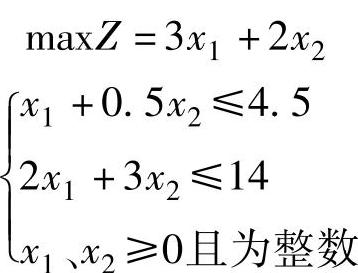
解 用图解法求解该线性规划问题，如图3-1所示。

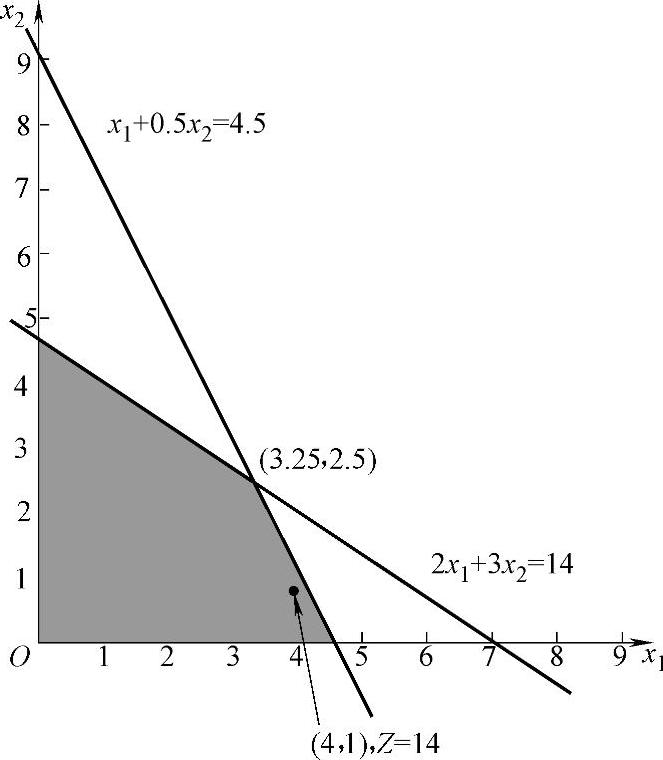
图3-1

如果不考虑x₁、x₂取整数的约束，用图解法求得最优解为X=（3.25，2.5）^T，图解法如图3-1所示。由于x₁、x₂必须取整数值，实际上问题的可行解集只是图中可行域内的那些整数点。用凑整法来解时需要比较四种组合，但X=（4，3）^T、X=（4，2）^T、X=（3，3）^T都不是可行解，X=（3，2）^T虽属可行解，但代入目标函数得Z=13，并非最优。实际上问题的最优解应该是X=（4，1）^T，Z^∗=14。这里可以注意到，（4，1）不是可行域的顶点，直接用图解法或单纯形法都无法找出整数规划问题的最优解来，因此整数规划的求解方法需要另行研究。

求解整数规划的常用的方法有完全枚举法、分支定界法、割平面法和隐枚举法。对于复杂的模型，完全枚举不是有效的算法，后面几种方法用得比较多。