参数分析是研究线性规划的资源限量与价值系数中附加了一个参数u，分析该参数在不同取值区间内最优解的变化情况，是研究最优解对于参数波动的一种灵敏度分析方法。

【例2.13】 线性规划

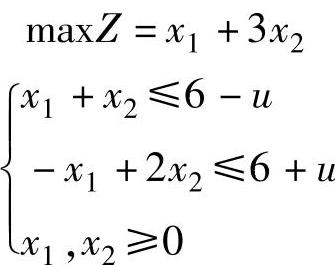
1）求参数u=0时的最优解；

2）讨论u∈[0，+∞）时最优解的变化。

解 1）当u=0时，加入松弛变量x₃、x₄后用单纯形法求解，最优表见表2-13。

表2-13

最优解X=（2，4，0，0）^T，最优值Z=14。

2）将约束条件右端分解成下列u的线性形式：

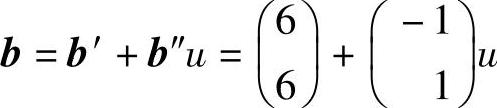
由灵敏度分析公式，计算最优表的常数项：

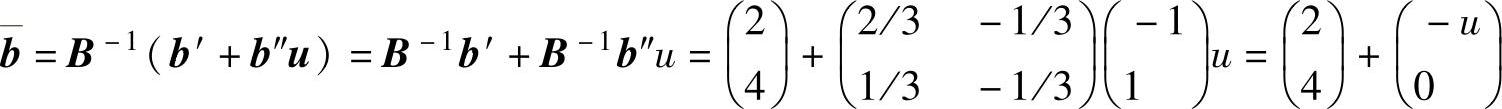
将此计算结果反映到最优表2-13得到带参数的单纯形表2-14。

表2-14

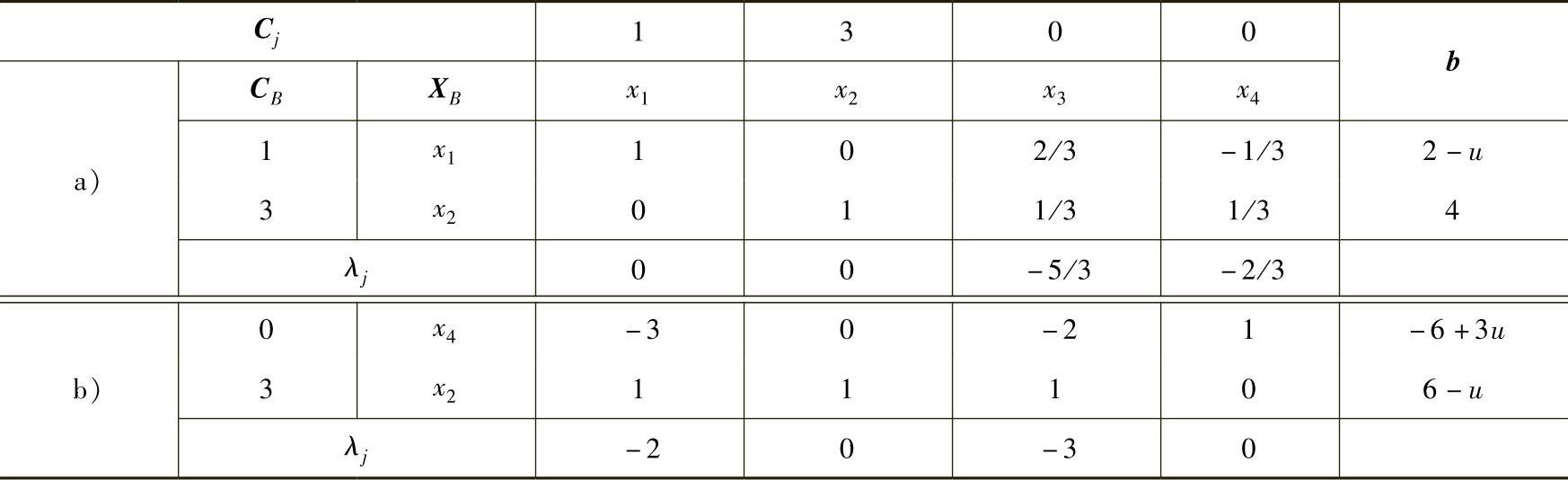
由表2-14a可知当0≤u≤2时，b≥0，该表即为最优表，最优解X=（2-u，4，0，0）^T。当u＞2时，b＜0，用对偶单纯形法求解得到表2-14b。

由表2-14b知，当u＞6时，该问题无可行解，当2≤u≤6时，最优解X=（0，6-u，0，-6+3u）^T。

同样，当目标函数中含有参数时，先令参数等于零，然后用灵敏度分析公式求出检验数，分析参数在不同区间内解的变化情况。

【例2.14】 已知Ⅰ、Ⅱ、Ⅲ三个道路工地要修建路基基层，由A、B、C三种货车向这三个工地运送砂砾，每种货车向各个工地运送1t材料所需的时间以及利润如表2-15所示。

表2-15

1）如何充分发挥车辆工作能力，使生产盈利最大。

2）若为了增加运输量，可借用其他公司的B型车辆，每月可借用60h，租金为1.8万元，问借用B型车辆是否合算。(www.daowen.com)

3）若有两个新的道路工地Ⅳ、Ⅴ，其中Ⅳ运输1t材料需用A车辆12h，B车辆5h，C车辆10h，每吨运输利润2.1千元；新产品Ⅴ需要A车辆4h，B车辆4h，C车辆12h，单位产品利润1.87千元。如果A、B、C车辆工作时间不增加，分别回答这两个工地修建路基基层是否合算。

4）现对Ⅰ道路工地进行迁移，迁移后为Ⅰ道路工地运送砂砾需用A车辆9h，B车辆12h，C车辆4h，每吨盈利4.5千元，问这对原计划有何影响。

解 1）设为分别为Ⅰ、Ⅱ、Ⅲ三个道路工地运送砂砾x₁、x₂、x₃吨，由题意可列出如下的线性规划模型

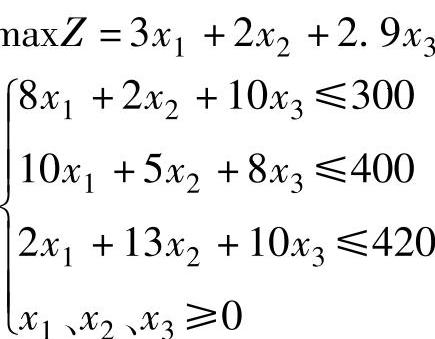
将上述问题变换为标准型得

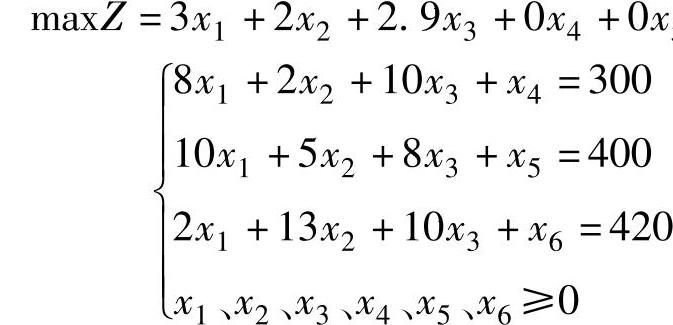
用单纯形法计算该问题过程见表2-16。

表2-16

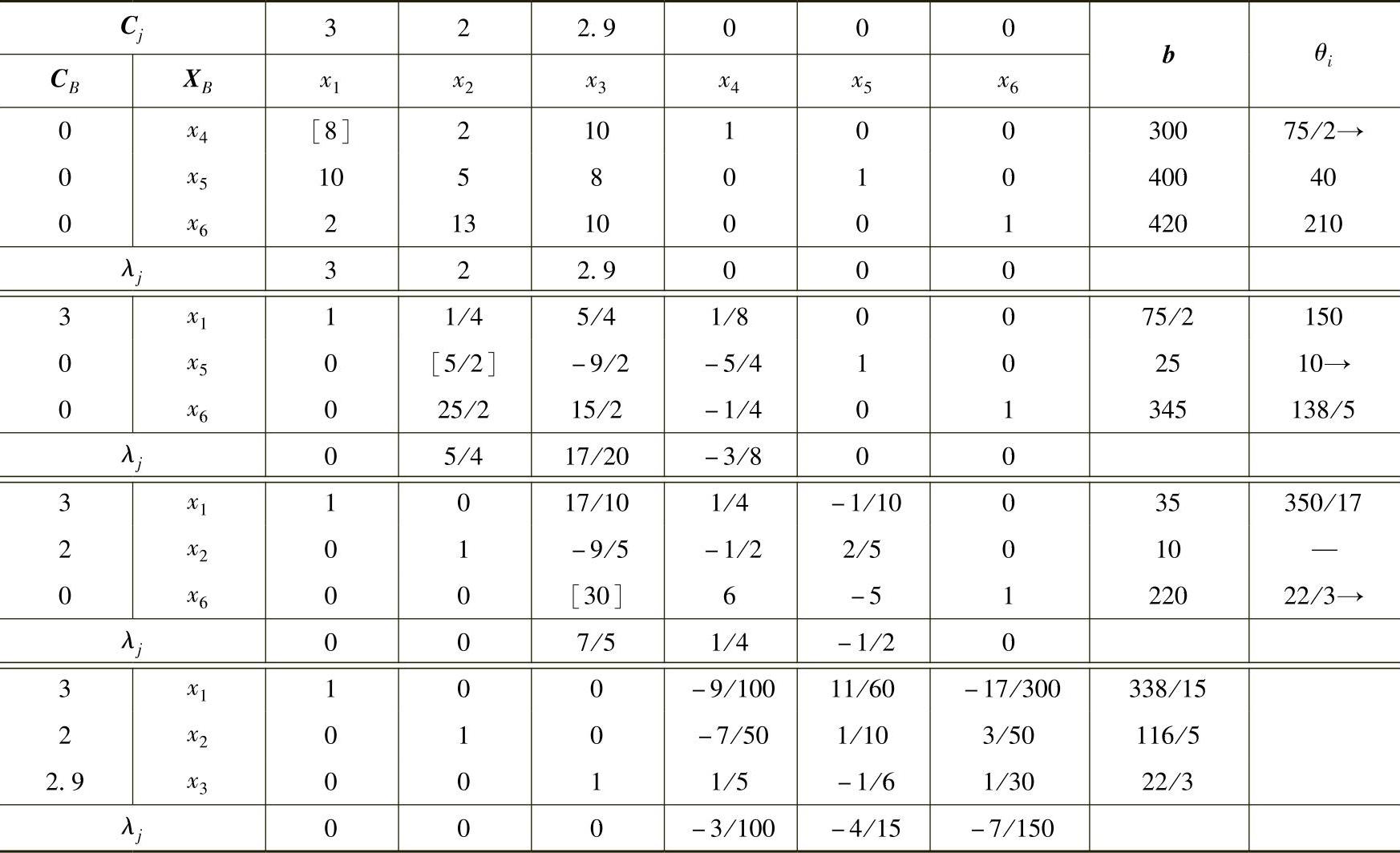
由表中计算结果可知该线性规划问题得最优解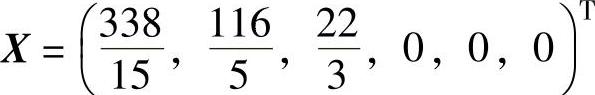，最优值。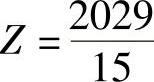

2）由最终单纯形表知，B型车辆的影子价格为4/15（千元/h），而借用B型车辆的租金为18/60=0.4>4/15，所以借用B型车辆不合算。

3）设为分别为Ⅳ、Ⅴ两个道路工地运送砂砾x₇、x₈吨，则x₇在最终单纯形表中的系数列向量

从而x₇在最终单纯形表中的检验数λ′₇=c₇-C_BB^-1P₈=1.87-（3，2，2.9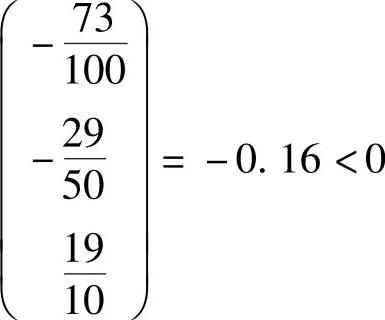），所以在Ⅳ道路上修建路基不合算。

x₈在最终单纯形表中的系数列向量

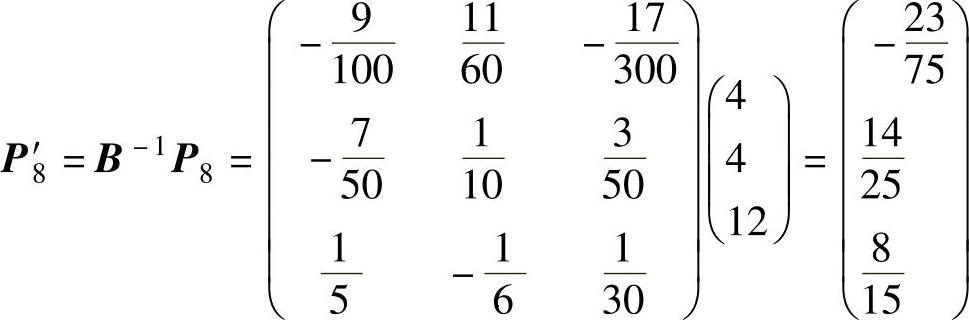
从而x₈在最终单纯形表中的检验数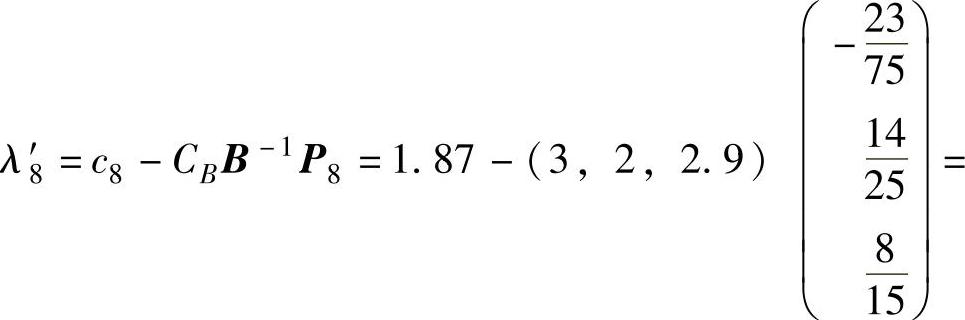0.12＞0，所以在Ⅴ道路上修建路基合算。

把x₈的系数列向量加入最终单纯形表，并进行迭代计算，计算过程见表2-17。

表2-17

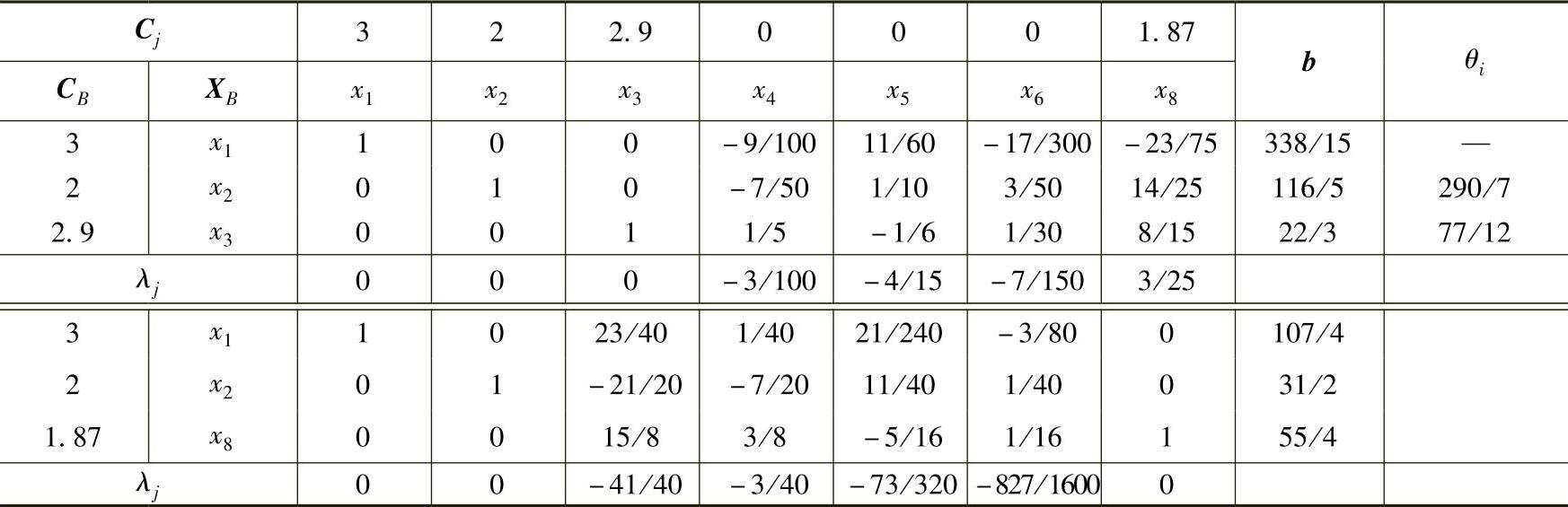
则线性规划问题的最优解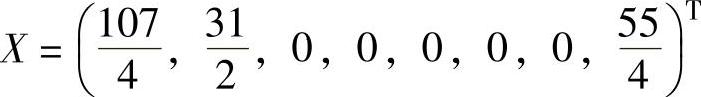，最优值。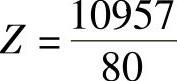

4）迁移后c₁=4.5，P₁=（9，12，4）^T，x₁在最终单纯形表中的检验数λ′₁=c₁-C₁B^-1P₁=0.843>0，所以迁移后能带来更多的经济效益。