资源限量的灵敏度分析：探究影响因素

设线性规划问题b_r的增量为Δb_r，则b的增量为Δb=（0，0，…，Δb_r，0，…，0）^T，在其他系数都不变的前提下，为使最优基B不变，求b_r的变化范围。

设线性规划：

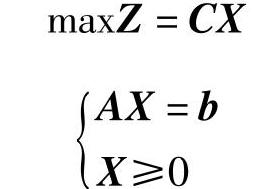
当b_r发生变化时，最优表中的检验数不变，要使最优基B不变，则要求新的最优解X′_B=B^-1b′＞0。

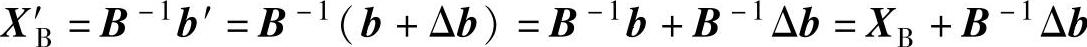
设最优基的逆矩阵：

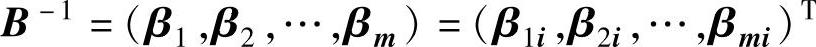
则式中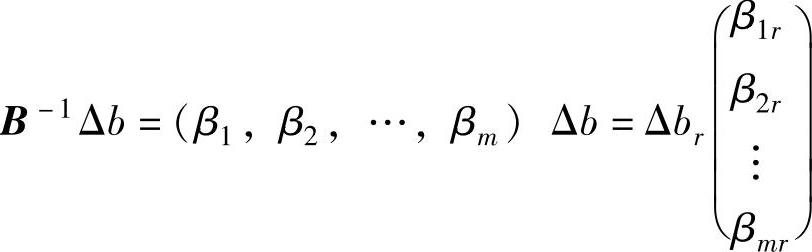，于是：

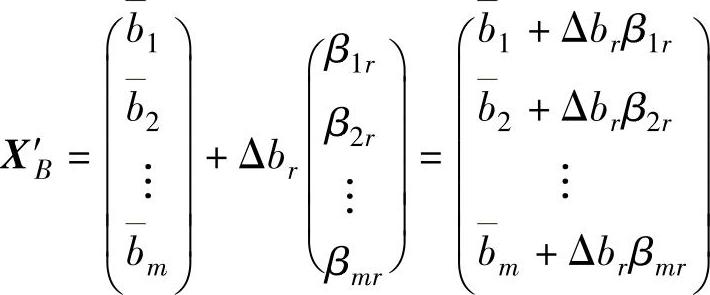
因此，使最优基不变，必须满足：

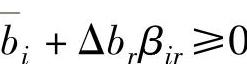
即当β_ir＞0时有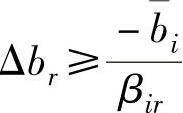，当β_ir＜0时有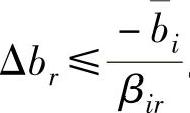。令

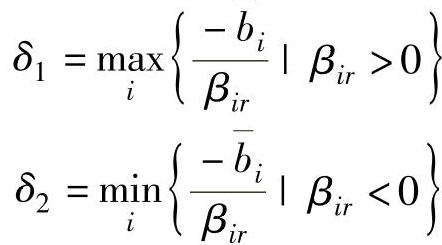
即必须满足：

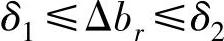
【例2.8】 已知线性规划

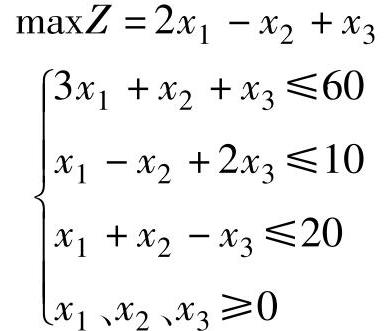(https://www.daowen.com)

分别求b₁、b₂、b₃的变化范围，使最优基不变。

解 加入松弛变量x₄、x₅、x₆，用单纯形法求解，最优表见表2-7。

表2-7

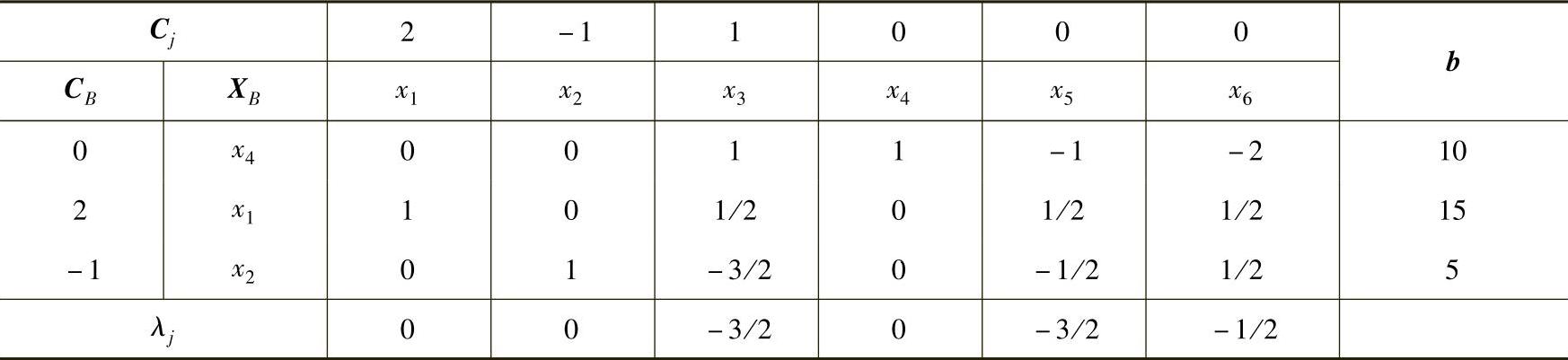
由表2-7可知，最优基B、B^-1、X_B分别为：

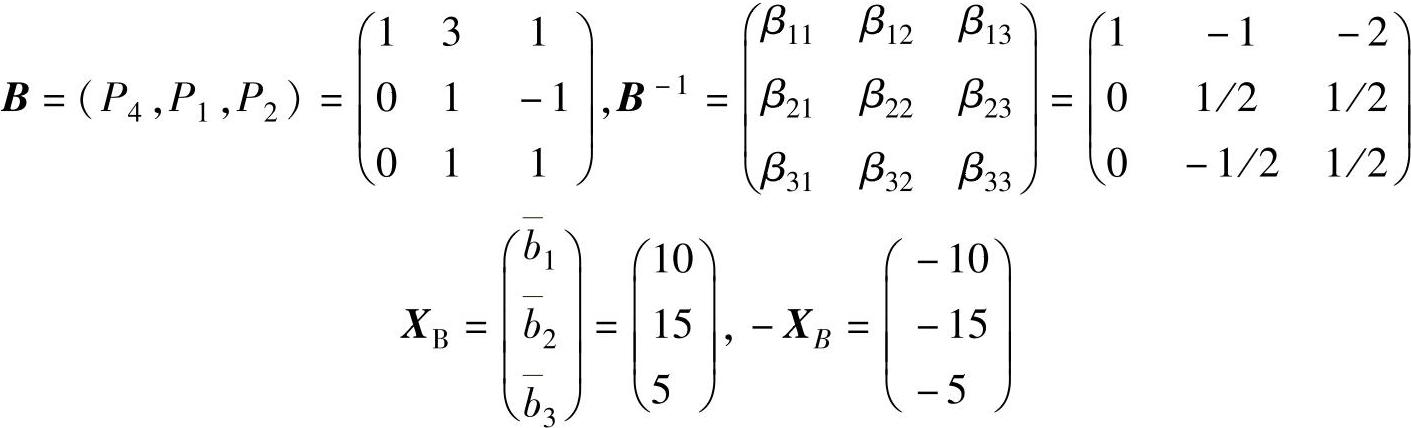
对于b₁，比值的分母取B^-1的第1列，这里只有β₁₁=1，β₂₁=β₃₁=0，则：

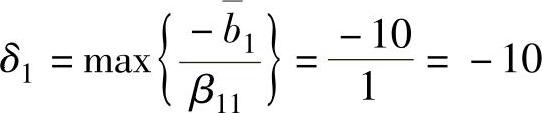
且Δb₁无上界，即Δb₁≥-10，所以b₁∈[50，+∞）时，最优基不变。

对于b₂，比值的分母取B^-1的第2列，β₁₂<0，β₃₂＜0，β₂₂＞0，则：

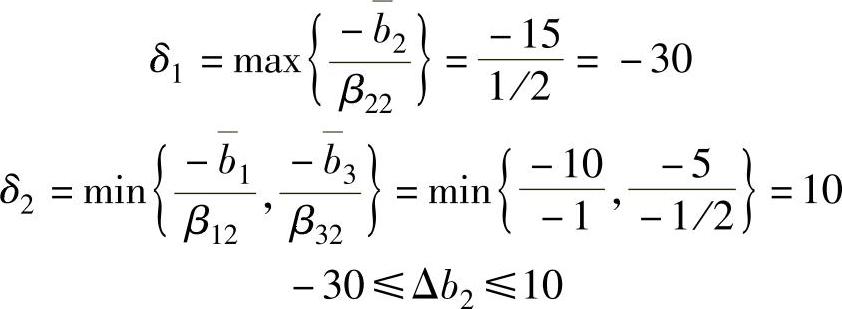
即b₂∈[-20，20]时，最优基不变。

对于b₃，比值的分母取B^-1的第3列，β₁₃<0，β₂₃＞0，β₃₃＞0，则：

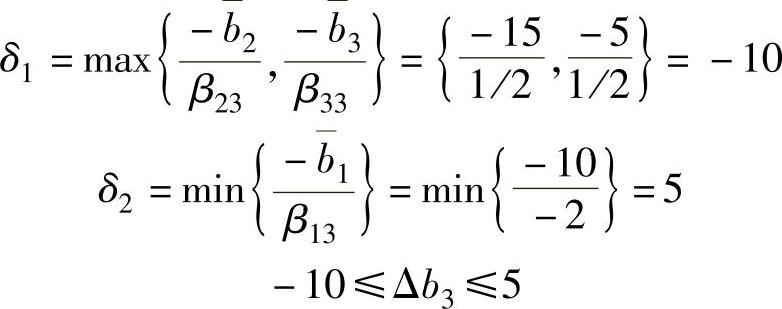
即b₃∈[10，25]时，最优基不变。