由性质2.6和例2.5可知，单纯形表迭代过程中，在b列得到的是原问题的基可行解，在检验数行得到的是对偶问题的基本解，因此（LP）和（DP）在求解迭代过程中有下列三种情况：1)(LP)的资源限量b,≥0且全部检验数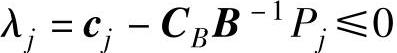，则有(DP)的检验数λ_i≥0且y_e≥0。这时（LP）与（DP）均达到最优解。

2）（LP）的资源限量b_i≥0，某个检验数λ_j>0，则有（DP）的某个变量y_j<0。这时（LP）可行，（DP）不可行。

3）（LP）中某个资源限量b_i＜0，全部检验数λ_j≤0，则有（DP）的检验数λ_i<0且全部y_j≥0。这时（LP）不可行，（DP）可行。

若线性规划出现第2）种情况，可用第1章介绍的单纯形法求解原问题。若线性规划出现第3）种情况，可保持对偶问题可行，即λ_j≤0，然后通过逐步迭代使原问题由不可行达到可行，这样就由情况3）变为情况1），也即得到了最优解。这种方法就是对偶单纯形法。

对偶单纯形法是求解线性规划的一种方法，而不是专门求解对偶问题的方法。它是根据对偶原理和单纯形法的原理而设计的，因而称为对偶单纯形法。

对偶单纯形法的条件是：

1）初始表中对偶问题可行，即极大化问题时λ_j≤0，极小化问题时λ_j≥0。

2）原问题不可行，即某个资源限量b_i<0。

由对偶单纯形法的条件可知，并不是所有的线性规划都适合用这种方法求解。从运算次数和速度看，该方法最适合于下列线性规划：

对偶单纯形法的计算步骤：

1）将线性规划的约束变换为等式，列出初始单纯形表。由于对偶问题可行，即λ_j≤0，当b_i≥0时，已得到最优解；若某个b_i<0，则进行迭代换基计算。

2）确定出基变量。按确定出基变量，即l行对应的变量x_l出基。

若不遵循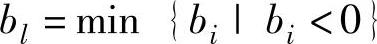规则，任选一个小于零的b对应的变量出基，不影响计算结果，只是迭代次数可能不一样。

3）确定进基变量。若x_l所在行的系数a_lj都非负，即全部a_lj≥0，说明原问题无可行解。若存在a_lj＜0，则按：

确定进基变量，选最小比值θ_K。列对应的变量X_K。进基。(www.daowen.com)

式中λ_j为非基变量的检验数，a_lj为出基变量x_l所在行的行系数。普通单纯形法的最小比值是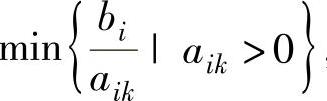，其目的是保证下一个原问题的基本解可行；对偶单纯形法的最小比值是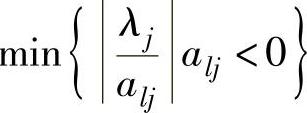，其目的是保证下一个对偶问题的基本解可行。

4）求新的基本解。以a_lk为主元素，按普通单纯形法在表中进行迭代运算，得到新的基本解，转到第1）步重复运算。

【例2.6】 求解线性规划

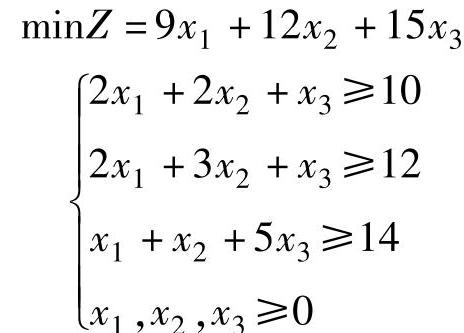
解 将约束不等式变换为等式，两边同乘以-1得到：

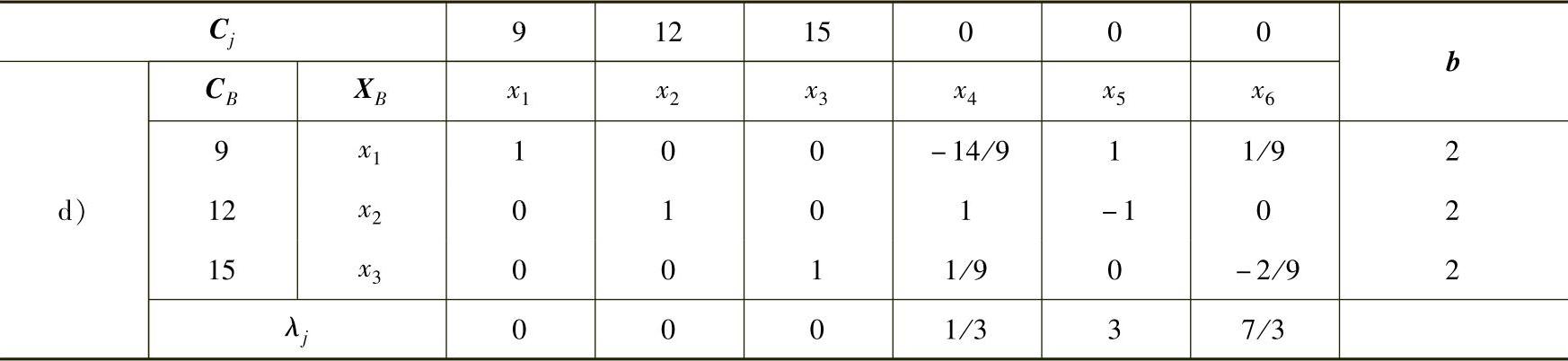
用单纯形法求解该问题时，由表2-5a中λ_j≥0可以看出该问题的对偶问题是可行的，由于b_i＜0，所以原问题不可行。因此要用对偶单纯形法求解该问题，见表2-5。

表2-5

（续）

【例2.7】 用单纯形法求解线性规划

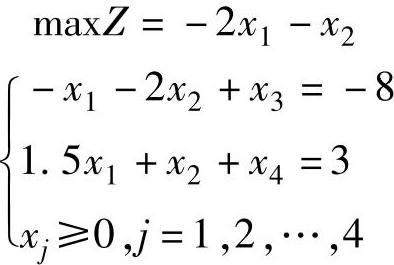
表2-6

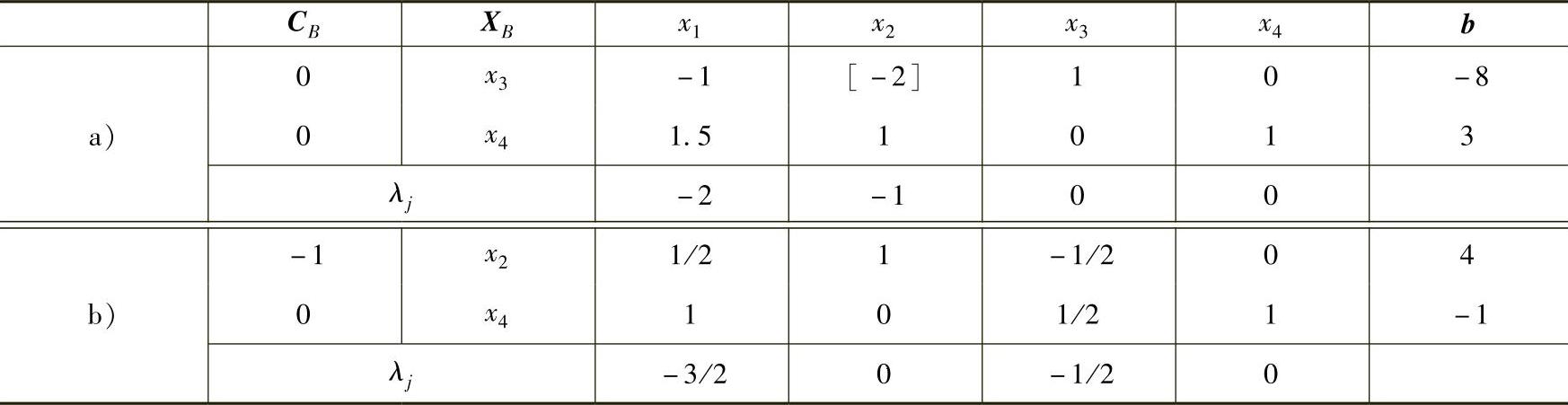
表2-6b中x₄=-1，但第2行的系数全部大于等于零，原问题无可行解。