为了讨论方便,设原问题与对偶问题都是规范形式,分别记为(LP)和(DP):
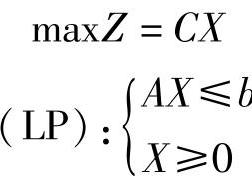
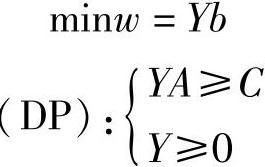
【性质2.1】 对称性。对偶问题的对偶是原问题。
证 设原问题是:
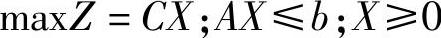
根据表2-1可写出它的对偶问题为:
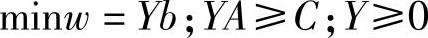
该问题等价于:
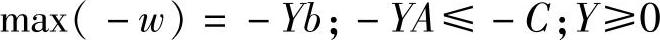
根据表2-1写出它的对偶问题为:
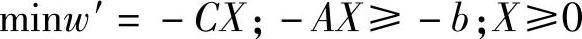
又该问题等价于:
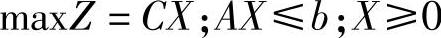
即对偶问题的对偶是原问题得证。
【性质2.2】 弱对偶性。若X∗、Y∗分别为(LP)和(DP)的可行解,则存在:CX∗≤Y∗b
证 因为X∗是(LP)的可行解,故有:
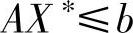
将该不等式两边左乘Y∗可得:
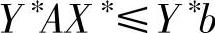
又因Y∗是(DP)的可行解,则有:
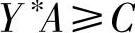
将该不等式两边右乘X∗可得:
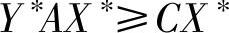
于是得到:
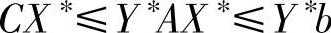
由该性质可得到下面几个结论:
1)(LP)的任一可行解的目标值是(DP)的目标值的下限,(DP)的任一可行解的目标值是(LP)目标值的上限。
2)如果一个问题有无界解,则其对偶问题无可行解。
3)如果原问题有可行解且其对偶问题无可行解,则原问题具有无界解。
注意:当一个问题无可行解时,其对偶问题可能有无界解,也可能无可行解。
【例2.3】 已知原问题(LP)和其对偶问题(DP)分别为:

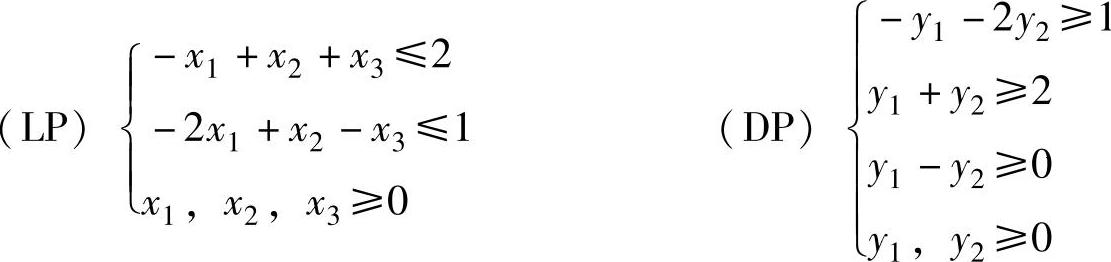
试用对偶理论证明原问题无界。
解 因为y1、y2≥0,则(DP)中的第一个约束条件不能成立,因此对偶问题无可行解。
通过观察可知X∗=(0,0,0)是(LP)的一个可行解,即原问题可行,则由结论3)可知原问题无界。
【性质2.3】 最优性。设X∗、Y∗分别为(LP)和(DP)的可行解,则X∗、Y∗是最优解,当且仅当CX∗=Y∗b。
证 设B是(LP)的最优基,若X∗、Y∗是最优解,则有:
Y∗=CBB-1且CX∗=CBB-1b=Y∗b
若CX∗=Y∗b,根据性质2.1,对任意可行解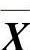 、
、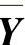 都有:
都有:
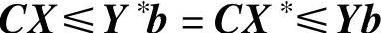
即CX∗是(LP)中任一可行解的目标值的上限,Y∗b是(DP)中任一可行解的目标值的下限,所以X∗、Y∗是最优解。
【性质2.4】 对偶定理。若(LP)有最优解,则(DP)也有最优解(反之亦然),且其最优值相等。
证 设B是(LP)的最优基,X∗是其最优解,则有:
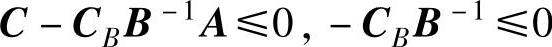
令Y∗=CBB-1,则有Y∗A≥C且Y∗≥0,即Y∗是(DP)的可行解。所以对目标函数有:
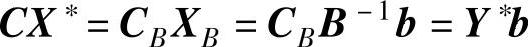
由性质2.3可知Y∗是(DP)的最优解。
由这个性质可得到结论:若(LP)和(DP)都有可行解,则两者都有最优解,若一个问题无最优解,则另一个问题也无最优解。
【性质2.5】 互补松弛性。设X∗、Y∗分别为(LP)和(DP)的可行解,XS和YS是它的松弛变量的可行解,则X∗、Y∗是最优解当且仅当YSX∗=0和Y∗XS=0。(www.daowen.com)
证 若X∗、Y∗分别为(LP)和(DP)的最优解,XS和YS是松弛变量,则有:
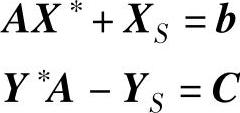
将第一式左乘Y∗,第二式右乘X∗得:
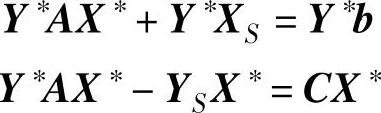
由性质2.3知,CX∗=Y∗b,得:
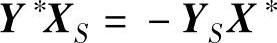
由于X∗、Y∗、XS、YS≥0,所以有:

反之,当YSX∗=0和Y∗XS=0时有:
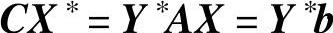
由性质2.3知X∗、Y∗是(LP)和(DP)的最优解。
通过该性质可知,当已知Y∗可求X∗或已知X∗可求Y∗。
YSX∗=0和Y∗XS=0两式称为互补松弛条件,可将其改写成:
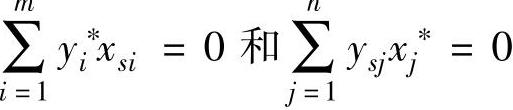
由于变量非负,要使上述等式成立,必定每一个分量都为零,则有:
1)当yi∗>0时,xsi=0;当xsi>0时yi∗=0。
2)当ysj>0时,xj∗=0;当xj∗>0时ysj=0。
利用上述关系,可建立对偶问题(或原问题)的约束线性方程组,方程组的解即为最优解。对于非规范形式,性质2.5仍然有效。
【例2.4】 已知线性规划
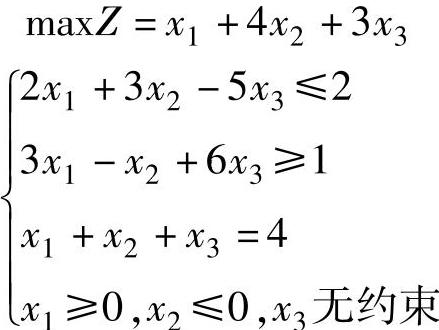
的最优解为X=(0,0,4)T,试求对偶问题的最优解。
解 对偶问题为:
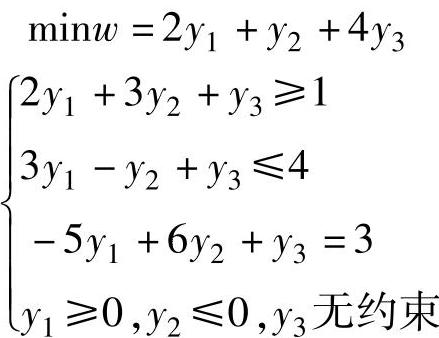
将X=(0,0,4)T代入原问题的约束中可知xs1≠0,xs2≠0。由互补松弛条件可得y1=y2=0,将其代入对偶问题的约束中可得y3=3。因此对偶问题的最优解Y=(0,0,3)T。
【性质2.6】 (LP)的检验数的相反数对应于(DP)的一组基本解,第j个决策变量xj的检验数的相反数对应于(DP)中第j个松弛变量ysj的解,第i个松弛变量xsi的检验数的相反数对应于第i个对偶变量yi的解。反之(DP)的检验数(不乘负号)对应于(LP)的一组基本解。
证 将原问题(LP)加入松弛变量XS变换为标准型。假设可行基B是矩阵A中的前m列,将变量和参数矩阵按基变量和非基变量对应分块,则有:
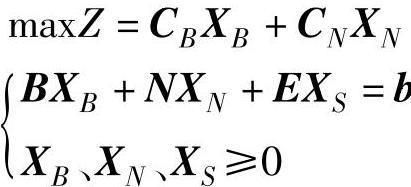
其对偶问题(DP)为:
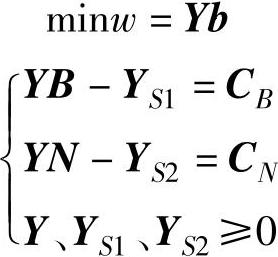
上述(LP)模型可用下面较简单的表2-2表达。用B-1左乘表2-2第二行得到表2-3第二行,再用(-CB)左乘表2-3第二行加上表2-2第三行得到表2-3第三行,即可求出该模型的基本可行解、检验数、目标函数值和单纯形乘子。
表2-2

表2-3

表2-3即为迭代后的单纯形表,由该表可知,对于任意可行基B,初始表中单位阵的位置经过迭代运算后,就是B-1的位置。
观察表2-3,当求得(LP)的一个可行解时,相应的检验数为0、CN-CBB-1N和-CBB-1,将Y=CBB-1代入对偶问题(DP)的约束条件中可得到:
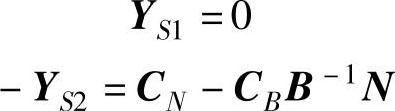
反之也用该方法证明。
性质2.6只适用于线性规划为规范形式的情况,性质2.1~2.5适用于所有线性规划问题。
【例2.5】 线性规划
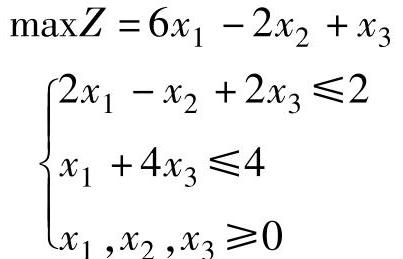
1)求该问题的最优解。
2)从最优表中写出对偶问题的最优解。
3)用公式Y=CBB-1求对偶问题的最优解。
解 1)加入松弛变量x4、x5后,用单纯形法求解,见表2-4,最优解X=(4,6,0)T。
2)设对偶变量为y1、y2,松弛变量为y3、y4、y5,则Y=(y1,y2,y3,y4,y5)。由性质2.6可知对偶问题的基本解(y1,y2,y3,y4,y5)=(-λ4,-λ5,-λ1,-λ2,-λ3)。因为表2-4c为最优解,所以Y(3)=(2,2,0,0,11)为对偶问题的最优解。
表2-4
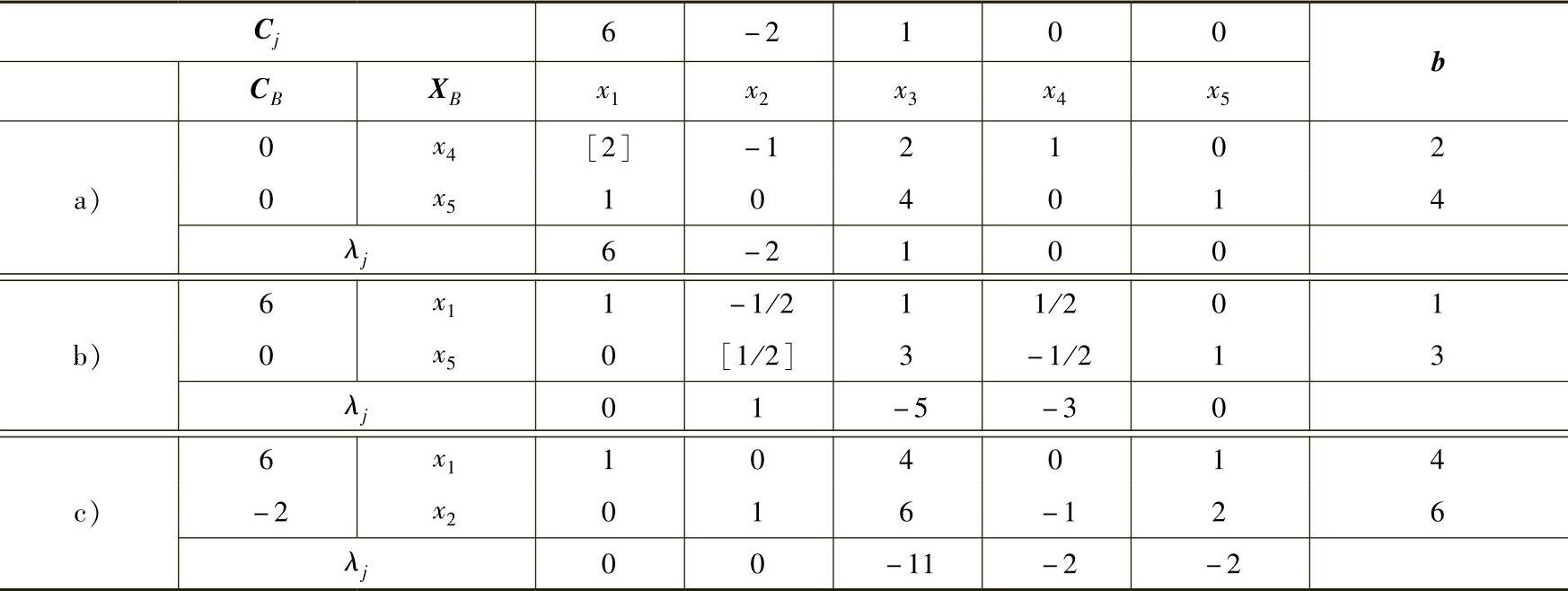
3)最优基为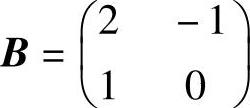 ,B-1为表2-4c中x4、x5两列的系数,即
,B-1为表2-4c中x4、x5两列的系数,即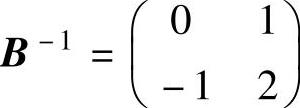 ,并且CB=(6,-2),所以对偶问题的最优解为:
,并且CB=(6,-2),所以对偶问题的最优解为:
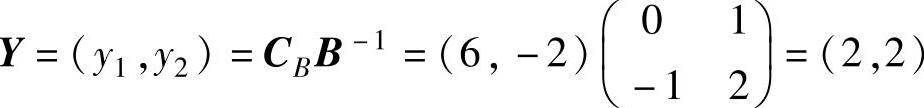
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







