1.线性规划的规范形式
求解原线性规划问题的对偶问题时,需将原线性规划问题变换为规范形式。规范形式(Canonical Form)又称对称形式,线性规划的规范形式为:
1)目标函数求极大值时,所有约束条件为≤号,变量非负。
2)目标函数求极小值时,所有约束条件为≥号,变量非负。
数学模型可表示为:

2.对称型对偶问题
设线性规划模型是式(2-1)的规范形式。当检验数
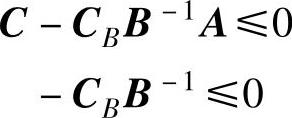
时得到最优解。
令Y=CBB-1,可得到:
Y≥0
由C-CBB-1A≤0得到:
YA≥C
在Y=CBB-1两边右乘b得到:
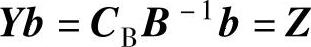
因为Y的上界为无限大,所以Yb=CBB-1b=Z只存在最小值,得到另一个线性规划问题为:

称其为原线性规划问题式(2-1)的对偶线性规划问题。
原问题和对偶问题是互为对偶的两个线性规划问题,规范形式的线性规划的对偶问题仍然是规范形式。根据原规范形式的线性规划问题中的系数矩阵A、C、b就可以求出它的对偶问题。
【例2.1】 写出下列线性规划的对偶问题。
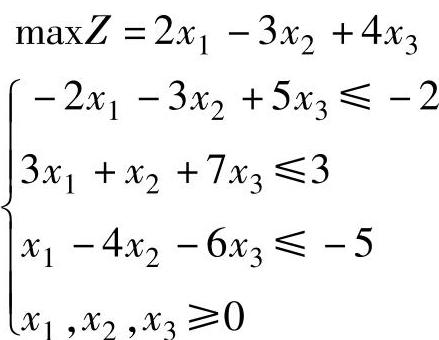
解 这是一个规范形式的线性规划,设Y=(y1,y2,y3),则有:
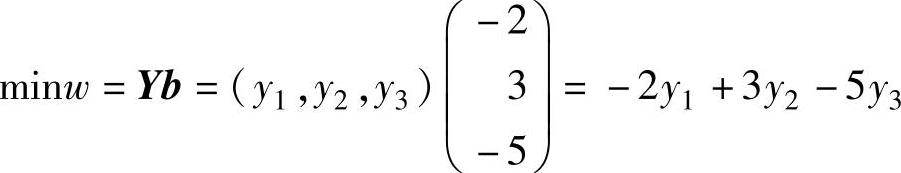
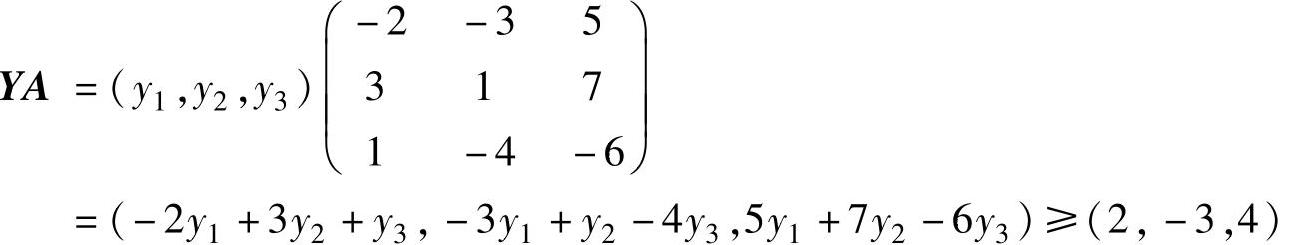
从而对偶问题为:
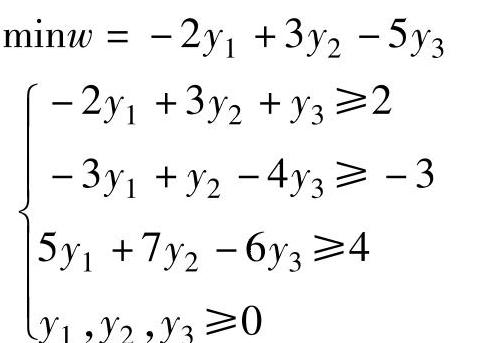
3.非对称型对偶问题
以上给出问题的形式是规范形式,若给出的线性规划不是规范形式,可以先变换成规范形式再写对偶问题。以原问题求最大值为例,非规范形式可能出现以下三种情况:
1)原问题第i个约束是“≥”约束,即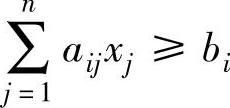 。
。
第一步:将该不等式两边同乘以-1,得到:
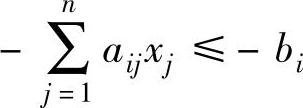
第二步:设该不等式对应的对偶变量为yi(yi≥0),则按对称形式变换关系可写出原问题的对偶问题为:
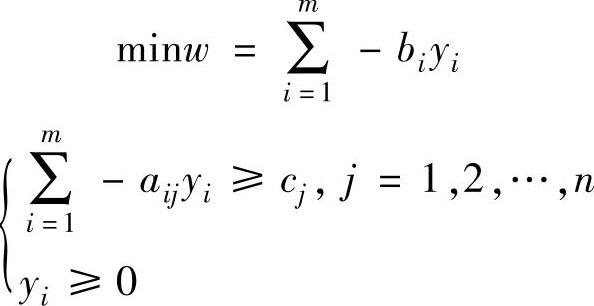
令y′i=-yi(y′i≤0),将y′i代入便可得到对偶问题:
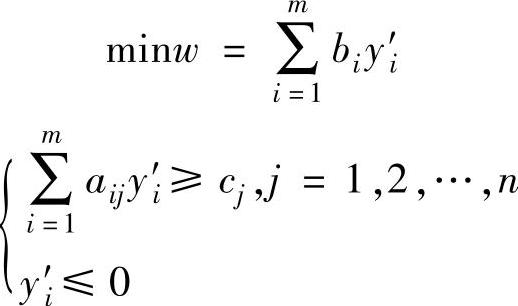
因此,当第i个约束为“≥”约束时,对应的第i个对偶变量y′i≤0。
2)原问题第i个约束中含有等式约束条件,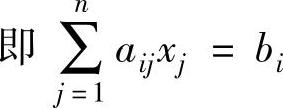 。
。
第一步:将该等式写成两个“≤”不等式为:(www.daowen.com)
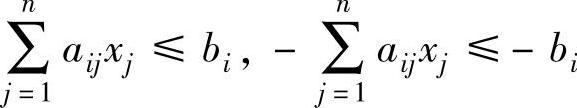
第二步:设不等式对应的对偶变量分别为y′i和y″i(y′i,y″i≥0),则按对称形式变换关系可写出原问题的对偶问题为:
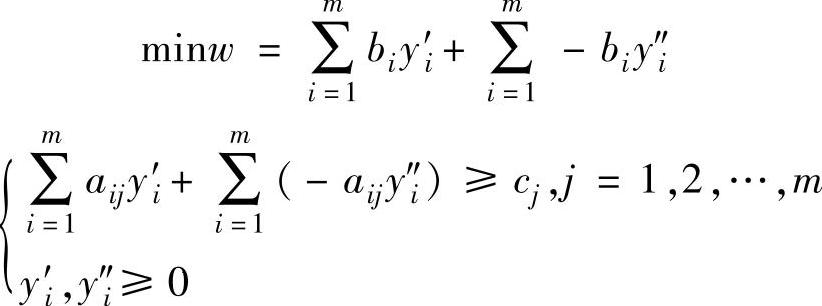
将上述线性规划问题整理后得到:
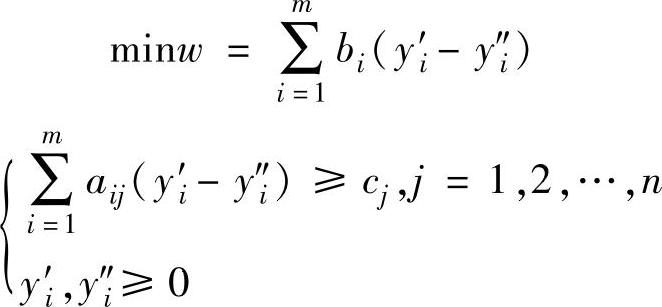
令yi=y′i-y″i,由此可见yi无符号限制,将yi代入便可得到对偶问题:
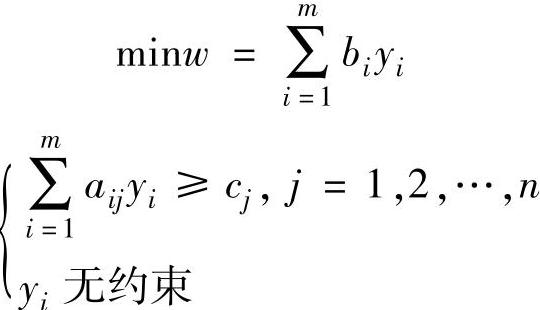
因此,当第i个约束为“=”约束时,对应的第i个对偶变量yi无符号约束。
3)原问题中xj≤0及xj无约束的情况。当xj≤0时,设对偶问题的变量为yi(yi≥0),
令xj=-xj′,xj′≥0,则对偶问题的第j约束条件为:
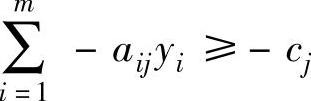
将该不等式两边同乘以-1得:
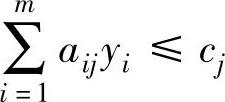
因此,当第j个变量xj≤0时,对应的第j个对偶约束为“≤”号。
当xj无约束时,设对偶问题的变量为yi(yi≥0),令xj=xj′-x″j(xj′,xj″≥0),则xj′和xj″对应的对偶约束为:
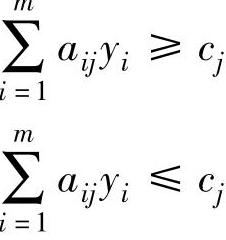
即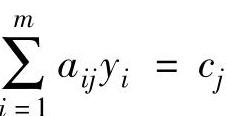
因此,当第j个变量xj无约束时,对应的第j个对偶约束为“=”号。
同理,原问题求最小值时,原问题和对偶问题的对应关系如下:
1)第i个约束为“≤”约束时,对应的第i个对偶变量yi≤0。
2)第i个约束为“=”约束时,对应的第i个对偶变量yi无符号约束。
3)当xj≤0时,对应的第j个对偶约束为“≥”约束;当xj无约束时,对应的第j个对偶约束为“=”约束。
综上所述,将原问题与对偶问题的对应关系列于表2-1。
表2-1
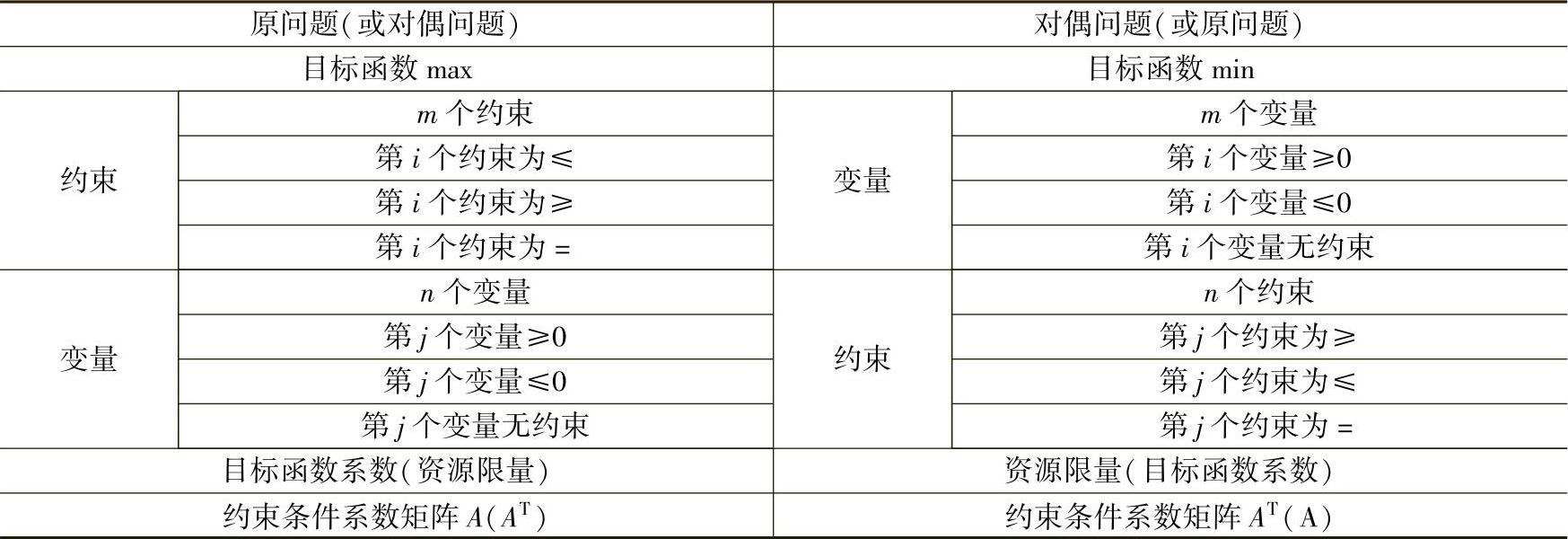
因此,解线性规划的对偶问题时的要点归纳如下:
1)两个问题,一个求极大化,一个求极小化。
2)两个问题的约束数和变量数互换。
3)两个问题的价值系数和资源限量互换。
4)两个问题的约束系数矩阵有互为转置的关系。
5)一个问题等式约束与另一个问题变量无约束相互对应。
6)一个问题约束(变量)的不等式符号与它的规范形式符号相反时,另一个问题变量(约束)的不等式符号与它的规范形式符号相反。
7)规范形式的线性规划的对偶仍然是规范形式。
【例2.2】 写出下列线性规划的对偶问题。
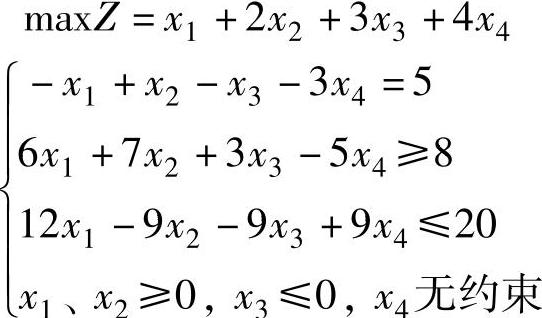
解 原问题目标函数求极大值,且有3个约束4个变量,则对偶问题应求极小值,且有3个变量4个约束,对照表2-1的对应关系,对偶问题为:
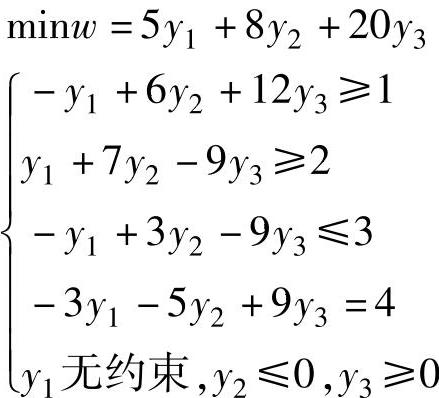
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







