在经济全球化的今天,道路交通扮演着重要角色,是支撑经济全球化的关键因素之一,也是推动我国经济发展的重要因素。近年来我国大力发展道路交通,在发展道路交通的过程中,如何降低施工、运输成本,增加运输收入等问题已经成为重点。而线性规划主要应用于解决最优化问题,下面举例说明线性规划在道路交通方面的应用。
【例1.18】 最小费用集合料问题。某筑路工地需10000m3混合集料作为道路基层,拟从附近两个弃土堆取料,从弃土堆A取料的装载运输费为1.0元/m3,从弃土堆B取料的装载运输费为1.4元/m3。问如何取料才使总的费用最少。已知弃土堆A的材料成分为:砂含量30%,砾石含量70%;弃土堆B的材料成分为:砂含量60%,砾石含量30%,粘土含量10%。混合集料的成分要求为:砂含量≥50%,砾石含量≤60%,粘土含量≤8%。
解 假设从弃土堆A、B所取的材料数量分别为x1、x2。工地需要的集料为10000m3,可表述为x1+x2=10000;混合集料中各种成分的含量应满足要求,这是限制条件,可分别表述为30%x1+60%x2≥50%(x1+x2),70%x1+30%x2≤60%(x1+x2),10%x2<8%(x1+x2)。由于从各个弃土堆所取的材料数量不能小于零,于是有x1、x2≥0。用Z表示费用,为使总费用最小,则有minZ=1.0x1+1.4x2。综合上述,这个问题的数学模型可归纳为:
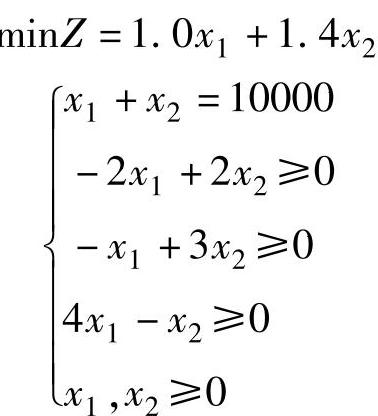
用图解法求解该线性规划问题得到最优解X=(3333,6667)T,最优值Z=12666(元)。
【例1.19】 截料优化问题。某桥梁工地要制作100套钢桁架,因构造要求,需将角钢截成3种不同规格的短料:2.9m、2.1m、1.5m。已知每根原料长7.4m,试问怎样截料才能使用料最少。
解 经分析将长7.4m的角钢截成上述所需3种不同规格的短料的方案有以下8种,见表1-16。
表1-16 下料方案
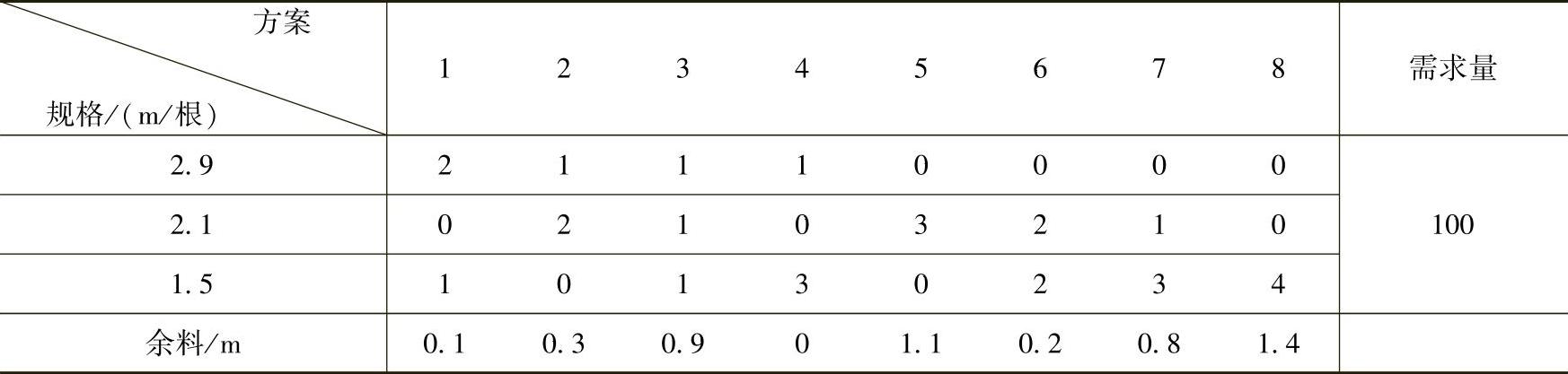
设xj(j=1,2,…,8)为第j种下料方案所用圆钢的根数。则用料最少的数学模型为:
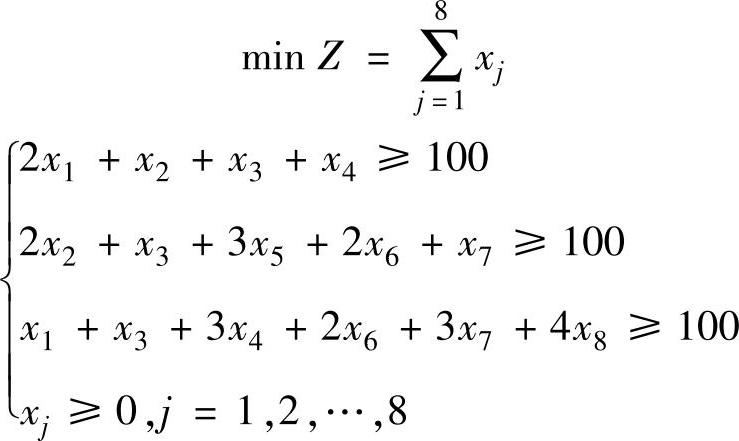
用单纯形法求解该线性规划问题得到最优解X=(10,50,0,30,0,0,0,0)T,最优值Z=90(根)。
【例1.20】 施工规划问题。某筑路工地同时对A、B两条公路开展压实工作,这两条路的宽度相同。A路采用静力碾压式压实机,B路采用振动式压实机,运行费用见表1-17。因为受机器碾压能力的限制,施工量不能超过5000m2/天,为了保证施工进度,要求A路每天的施工量≥800m2,B路每天的施工量≥1500m2。该工地有12名机械手可操作两种压实机。试问如何分配这几名机械手,才能使每天的运行费用最低。
表1-17 运行费用

解 设分配给静力碾压式压实机、振动式压实机的机械手人数分别为x1、x2,那么每天的总运行费用为:
Z=400x1+1000x2
受压实机工作能力的限制,则应有:
100x1+500x2≤5000
为了满足施工进度,则应有:
100x1≥800,500x2≥1500
受机械手人数的限制,则应有:
x1+x2≤12
综上所述,使每天的运行费用最低的数学模型为:
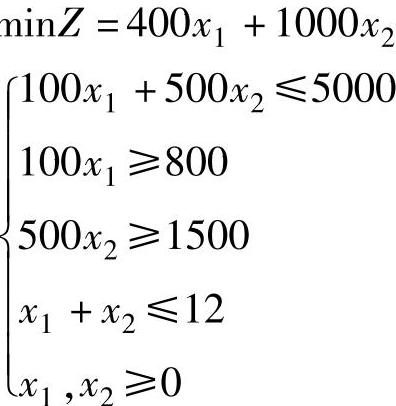
用单纯形法求解该线性规划问题得到最优解X=(8,4)T,最优值Z=7200(元)。
【例1.21】 多阶段投资问题。某客运公司在今后五年内考虑将10万元资金给下列项目投资,已知:
项目A:从第1年到第4年每年年初需要投资,并于次年末回收本利115%。
项目B:第3年初需要投资,到第5年末能回收本利125%,但规定最大投资额不超过4万元。
项目C:第2年初需要投资,到第5年末能回收本利140%,但规定最大投资额不超过3万元。(www.daowen.com)
项目D:4年内每年初可购买公债,于当年末归还,并加利息6%。
试问应如何投资能使第5年末拥有资金的本利总额为最大。
解1)确定变量 以xiA,xiB,xiC,xiD(i=1,2,…,5)分别表示第i年年初给项目A、B、C、D的投资额。根据给定的条件,将变量列于表1-18中。
表1-18 变量列表

2)目标函数 问题是要求在第5年末该客运公司手中拥有资金额达到最大,则目标函数可表示为:
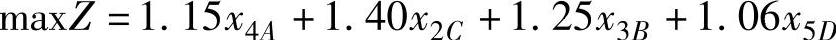
3)投资额应等于手中拥有的资金额 由于项目D每年都可以投资,并且当年年末即能回收本息。所以该客运公司每年应把资金全部投出去。
第1年:该部门年初拥有100000元,所以有
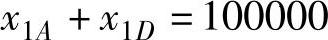
第2年:因第1年给项目A的投资要到第2年年末才能回收。所以该客运公司在第2年年初拥有的资金额仅为项目D在第1年回收的本息x1D(1+6%)。于是第2年的投资分配是
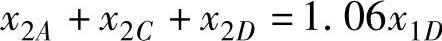
第3年:第3年年初的资金额是从项目A第1年投资及项目D第2年投资中回收的本利总和:x1A(1+15%)及x2D(1+6%)。于是第3年的资金分配是
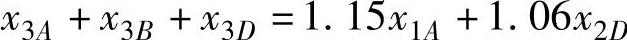
第4年:同上分析,可得
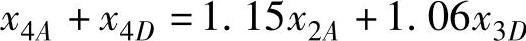
第5年:
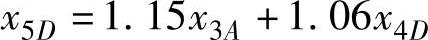
此外,由于对项目B、C的投资有限额的规定,则有
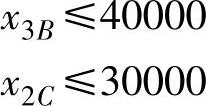
4)数学模型 经过以上分析,这个与时间有关的投资问题可以用以下线性规划模型来描述:
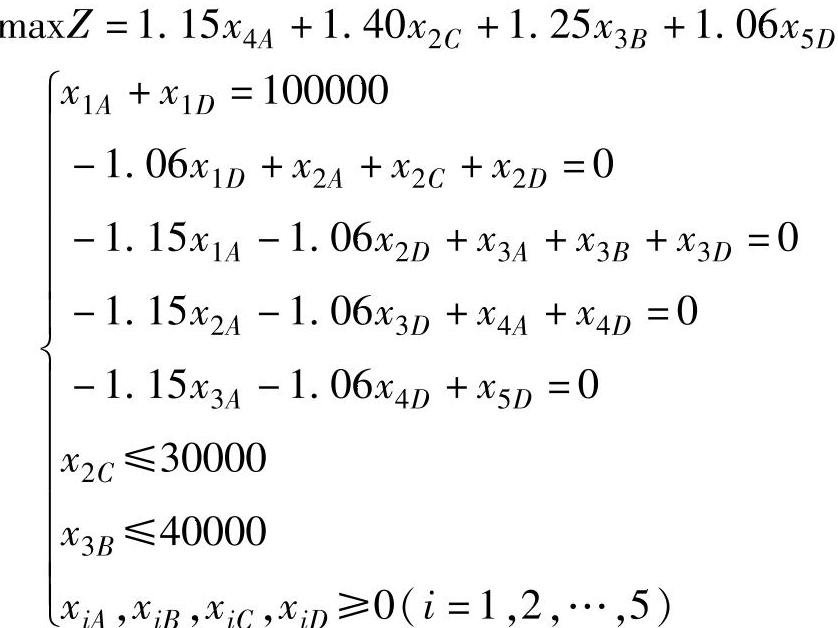
5)用单纯形法计算得最佳投资为
第1年:x1A=34783,x1D=65217
第2年:x2A=39130,x2C=30000,x2D=0
第3年:x3A=0,x3B=40000,x3D=0
第4年:x4A=45000,x4D=0
第5年:x5D=0
到第5年末该部门拥有资金总额为143750,盈利43.75%。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







