1.大M单纯形法

【例1.12】 用单纯形法求解下列线性规划

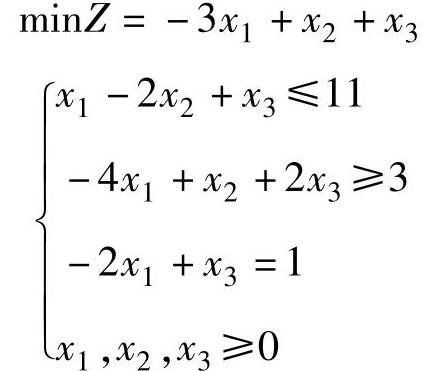
解 将数学模型变换为标准型：

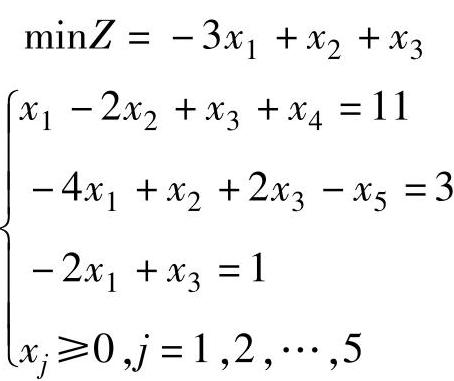
从等式约束条件可见，不管用哪些变量作为基变量，都不能构成单位系数矩阵，故需在第二、三约束中分别加入人工变量x₆、x₇，目标函数中加入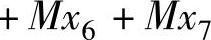一项，得到大M单纯形法数学模型：

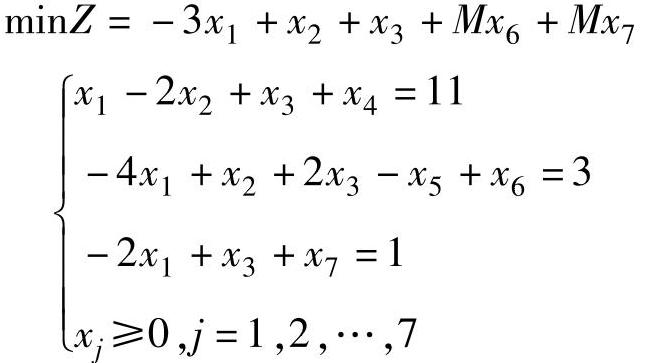
接下来用前面介绍的单纯形法求解，见表1-7。

表1-7

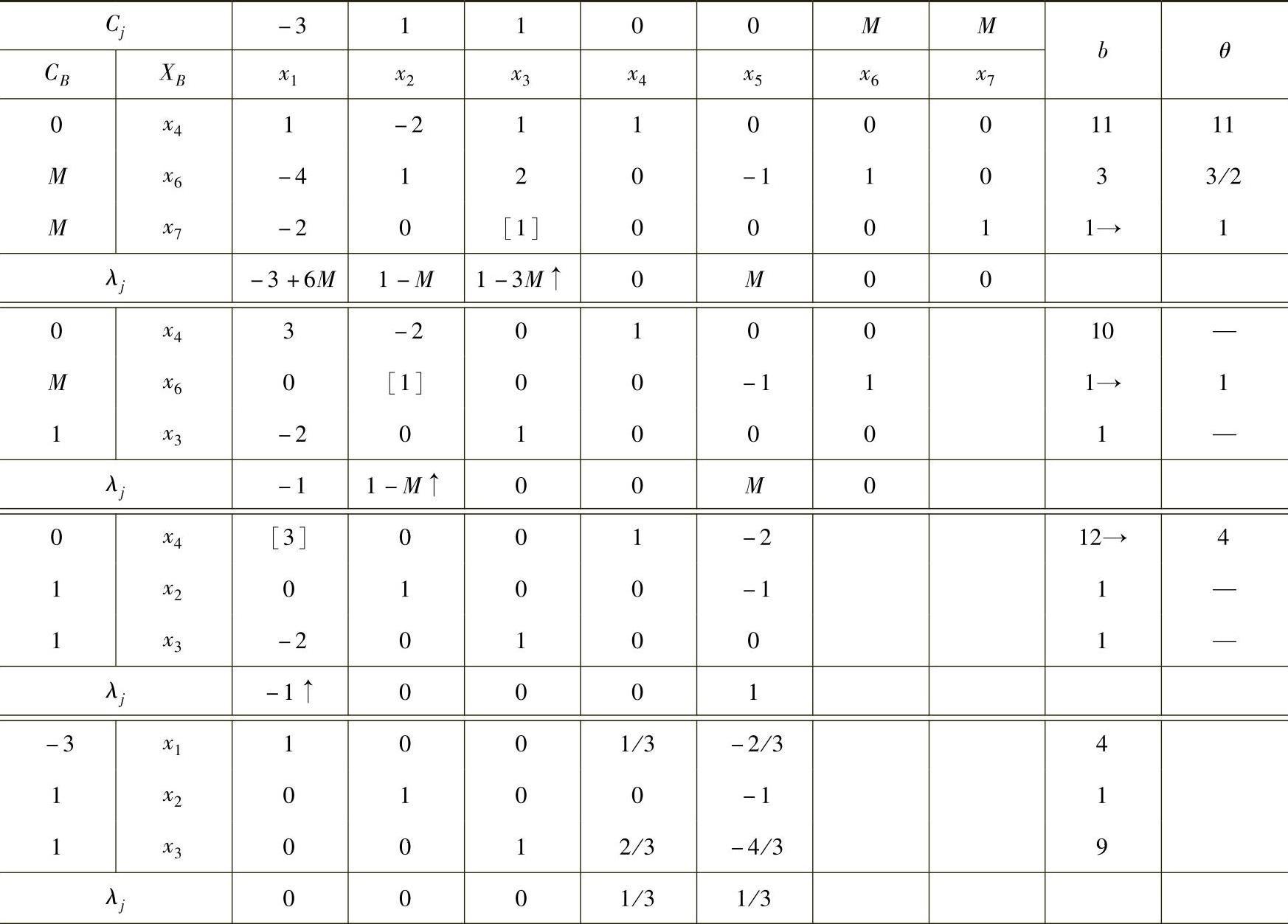
因为本例是求最小值，所以当λ_j≥0且x₆、x₇为非基变量时，可求得最优解为X=（4，1，9，0，0）^T，最优值Z=-2。

观察表1-7可知，人工变量是帮助寻求原问题的可行基，第三张表就找到了原问题的一组基变量x₄、x₂、x₃。在迭代过程中为了实现目标函数的最大化或者最小化，必须把人工变量从基变量换出，即R_i要出基。表1-7的第三张表中原问题的一组基变量为x₄、x₂、x₃，此时人工变量从模型中退出，也说明原问题具有可行解，但不一定具有最优解。如果用大M单纯形法计算得到最优解中存在R_i＞0，则表明原线性规划问题无可行解。

需要注意的是：约束条件加入人工变量后，求极大值时，将目标函数变为maxZ=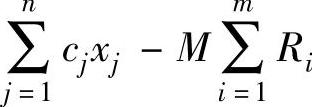；求极小值时，将目标函数变为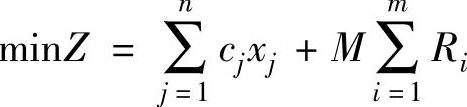。为了使人工变量不影响目标函数的取值，式中M为任意大的正数。

【例1.13】 求解线性规划

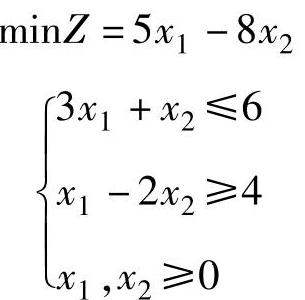
解 将数学模型变换为标准形式

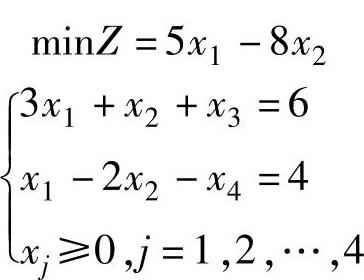
由于该标准型中系数矩阵没有2×2阶单位矩阵，因此需要在第二个方程中加入人工变量x₅，目标函数中加上Mx₅，得到

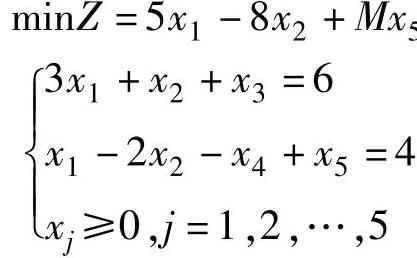
用单纯形法计算如表1-8所示。

表1-8

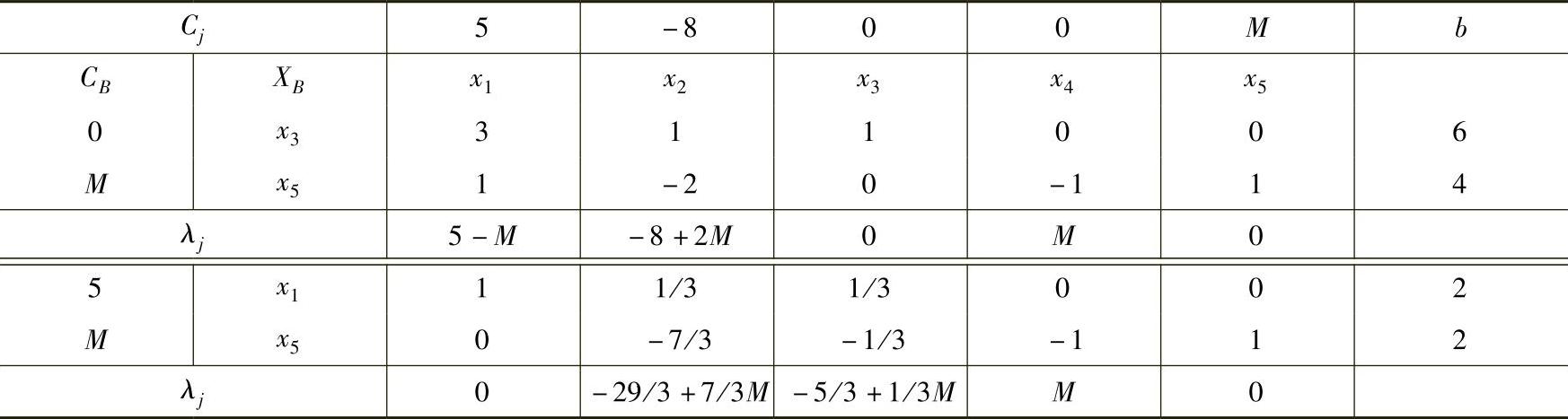
因此该问题的最优解X=（2，0，0，02）^T，最优Z=10+2M。由于最优解中含有人工变量x₅≠0，说明这个解是伪最优解，是不可行的，也即原问题无可行解。

2.两阶段单纯形法

两阶段单纯形法与大M单纯形法的目的类似，将人工变量从基变量中换出，以求得原问题的初始基本可行解。将问题分为以下两个阶段。

第一阶段：给原线性规划问题加入人工变量，构造仅含人工变量的目标函数并实现其最小化，即。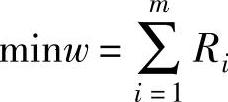

第二阶段：将第一阶段计算得到的最终表除去人工变量，并且将目标函数行的系数换为原问题的目标函数系数，作为第二阶段计算的初始表。(www.daowen.com)

当第一阶段的最优解w=0时，说明找到了原问题的一组基本可行解；反之当w≠0时，说明还有不为零的人工变量是基变量，则原问题无可行解。

【例1.14】 用两阶段单纯形法求解例1.12的线性规划。

解 标准型为

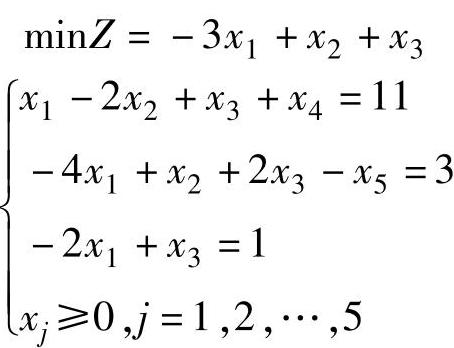
在第二、三约束中分别加入人工变量x₆、x₇后，构造第一阶段问题：

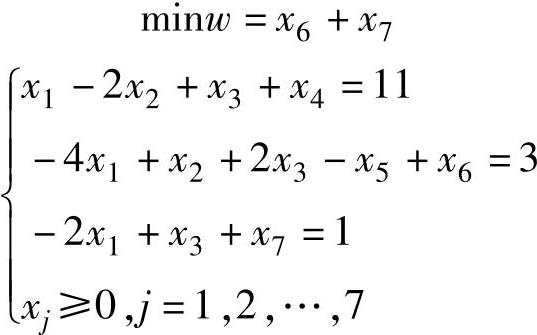
用单纯形法求解，得到第一阶段问题的计算表1-9。

表1-9

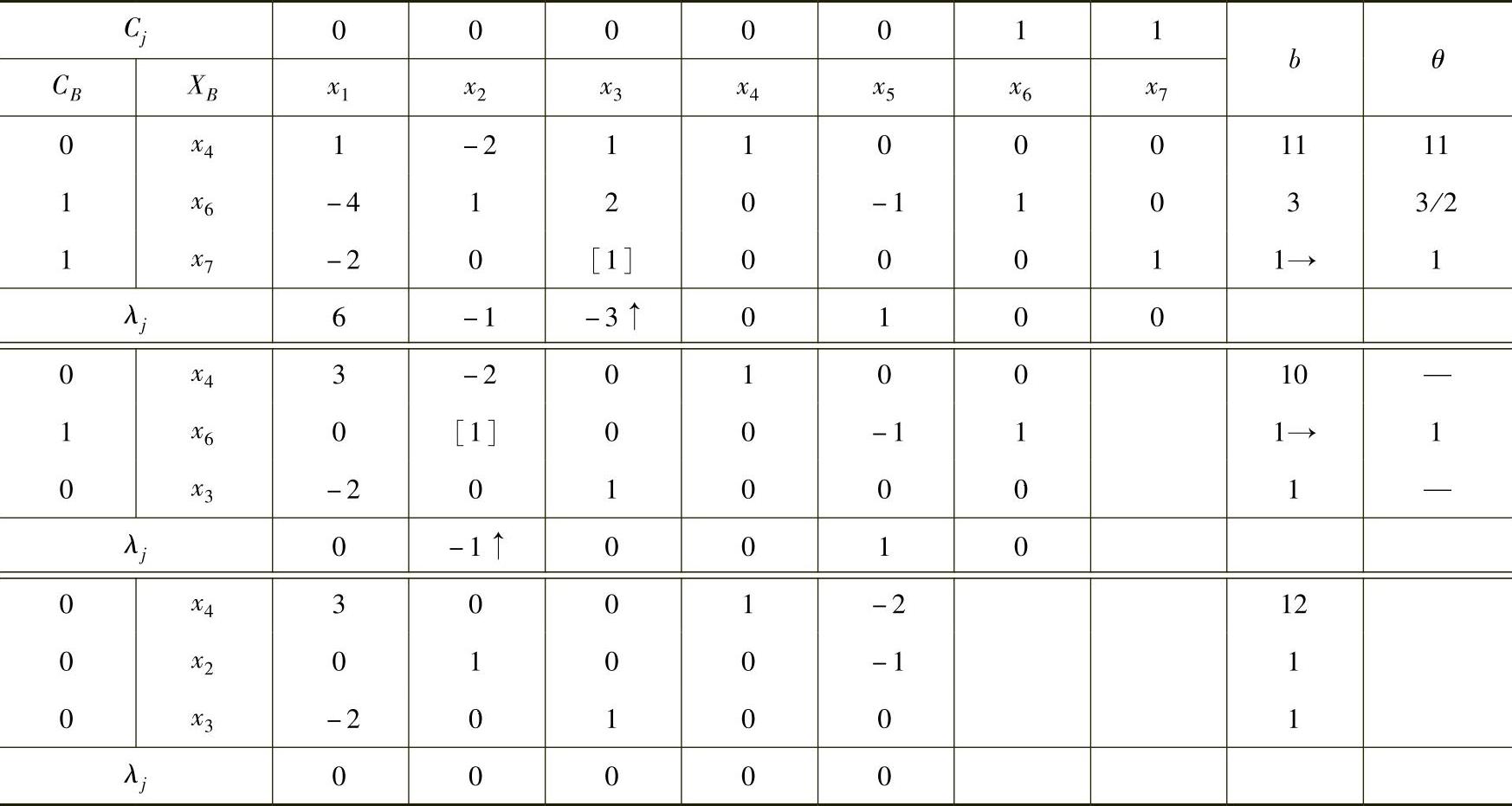
最优解为X=（0，1，1，12，0）^T，最优值w=0。第一阶段最后一张最优表说明找到了原问题的一组基本可行解，将它作为初始基本可行解，进行第二阶段的计算，见表1-10。

表1-10

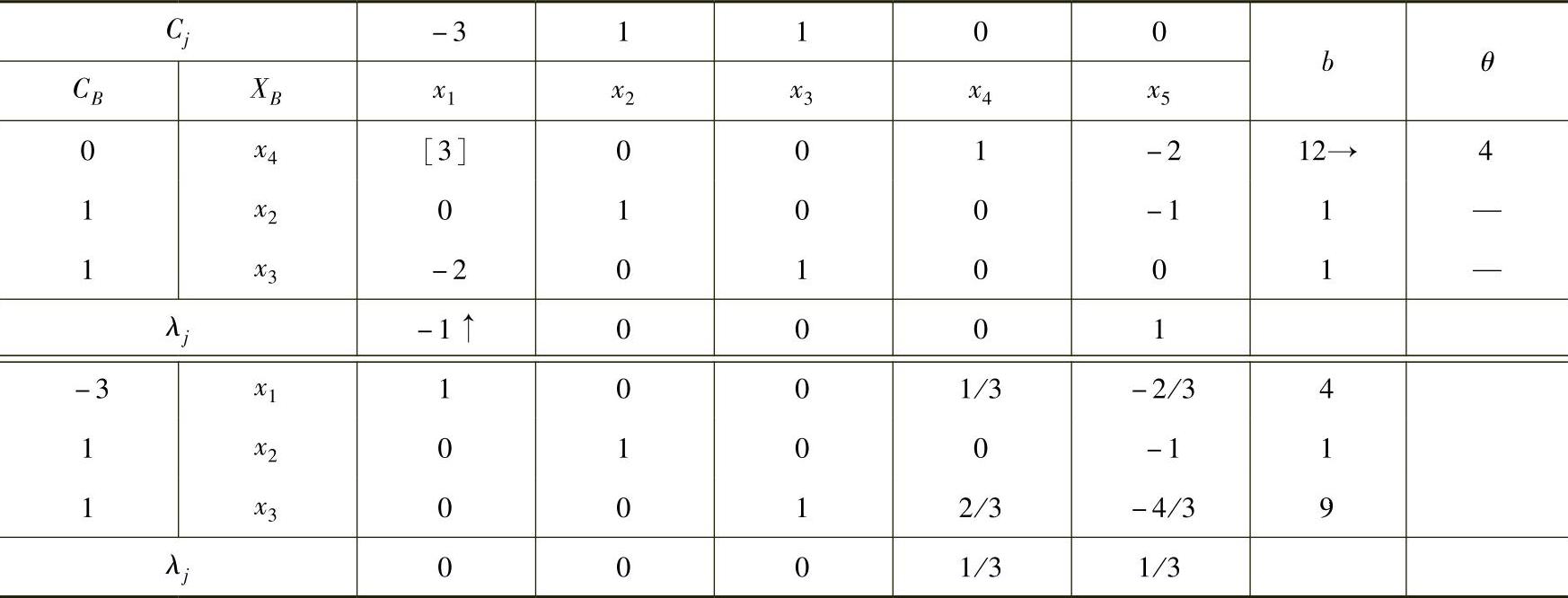
最优解为X=（4，1，9，0，0）^T，最优值Z=-2。

在第二阶段计算时，初始表中的检验数不能引用第一阶段最优表的检验数，必须换成原问题的检验数，可用公式计算。此外，即使第一阶段最优值w=0，也只能说明原问题有可行解，第二阶段问题不一定有最优解，即原问题可能有无界解。

从例1.12和例1.14可以看出，大M单纯形法和两阶段单纯形法每一步迭代的方法类似，最后结果相同。

【例1.15】 用两阶段法求解例1.13的线性规划。

解 第一阶段为

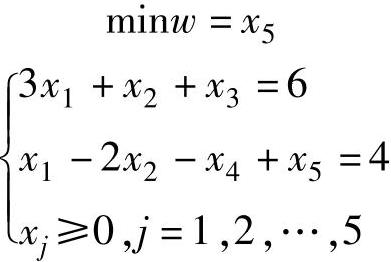
用单纯形法计算，如表1-11所示。

表1-11

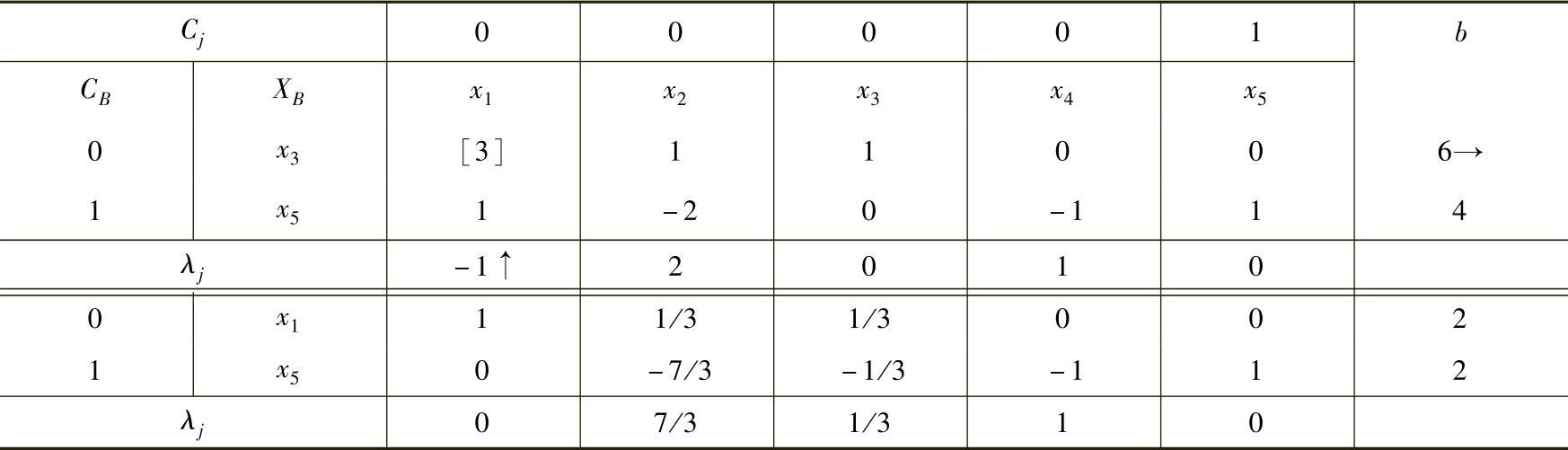
最优解为X=（2，0，0，0，2）^T，最优值w=2≠0，x₅在基变量中，则原问题无可行解。

综上所述，当出现以下两种情况，原问题无可行解：

1）大M法求解时，最优解中含有不为零的人工变量。

2）两阶段法计算时，第一阶段的最优值w≠0。