单纯形法是求解线性规划问题最主要的一种方法。根据上述线性规划问题的基本定理可知，目标函数的最大值在可行域的某一个顶点达到，而且顶点个数有限。单纯形法的指导思想就是先任取一个顶点X^（1），代入目标函数得Z₁，然后在顶点X^（1）的基础上换一个顶点X^（2），使得Z₂>Z₁，这样一次次迭代，经有限个步骤就可求得使目标函数达到最大值的点，于是就得到线性规划问题的最优解，这种迭代过程就是从一个顶点移动到另一个邻近顶点的过程。

【例1.8】 用单纯形法求下列线性规划的最优解：

maxZ=3x₁+4x₂

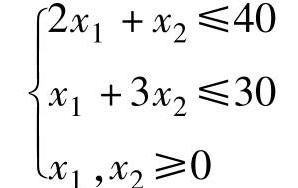
解

1）变换为标准型

maxZ=3x₁+4x₂

2）找初始基本可行解 该问题的系数矩阵为：

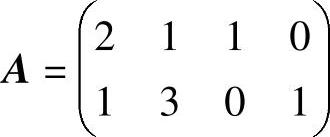
A中第3列和第4列组成二阶单位矩阵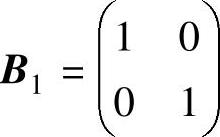，r（B₁）=2，则B₁是一个初始基，由此得到一个初始基本可行解为X^（1）=（0，0，40，30）^T。

3）检验X（1）是否为最优解 分析目标函数maxZ=3x₁+4x₂可知，非基变量x₁，x₂的系数都是正数，若x₁，x₂为正数，则Z值就会增加。所以X（1）不是该问题的最优解。因此，只要在目标函数的表达式中还存在有正系数的非基变量，目标函数值就有增加的可能，就需要将非基变量与基变量进行对换，即可行解必须从该顶点移到另一个顶点。判别线性规划问题是否达到最优解的数称为检验数，记为λ_j（j=1，2，…，n）。本例中λ₁=3，λ₂=4，λ₃=0，λ₄=0。

检验数：目标函数用非基变量表示，其变量的系数为检验数。

4）第一次换基迭代 在此需要选择一个λ_k>0的非基变量x_k换成基变量，称为进基变量，同时选择一个能使所有变量非负的基变量x_i换成非基变量，称为出基变量。一般选择对应的x_k进基，本例中x₂进基。由于x₂进基，必须要从原基变量x₃、x₄中选择一个换出作为非基变量，并且使得新的基本解仍然可行。由约束条件

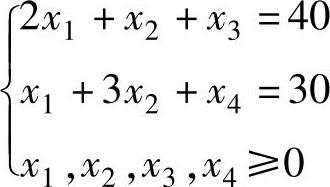
知，当x₁=0时，可得到如下不等式组

因此x₂只有选择x₂=min（40，10）=10时，才能使上述不等式组成立。又因为非基变量等于零，当x₂=10时，x₄=0，即x₄为出基变量。

用线性方程组的消元法（初等行变换），将基变量x₂、x₃解出得到：

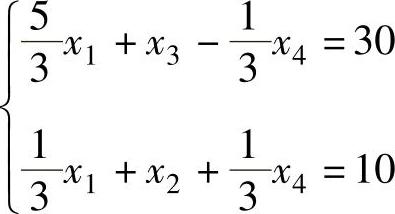
解得另一个基本可行解为：

X^（2）=（0，10，30，0）^T5）检验X^（2）是否为最优解 X^（2）是不是最优解，仍要看检验数的符号。由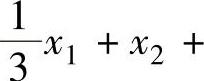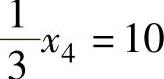得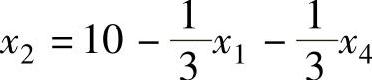，代入目标函数得：

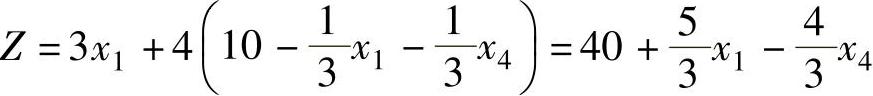
目标函数中非基变量的检验数。因为λ₁>0，所以X^（2）不是最优解。

6）第二次换基迭代 迭代方法同上面的相同，x₁为进基变量，选择出基变量用最小比值规则，即常数向量与进基变量的系数列向量的正数求比值，最小比值对应的变量出基。本例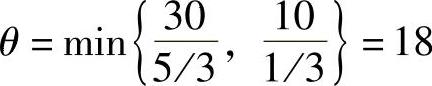，第一行的比值最小，x₃为出基变量。因此x₁、x₂为基变量，x₃、x₄为非基变量。

将x₁、x₂的系数矩阵用初等变换的方法变换为单位矩阵（或消元法解出x₁、x₂）得到：

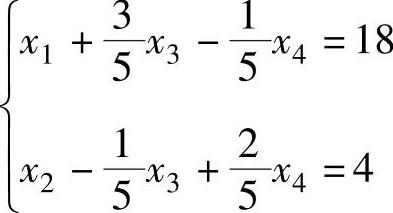
解得另一个基本可行解为：

X^（3）=（18，4，0，0）^T

7）检验X^（3）是否为最优解 由知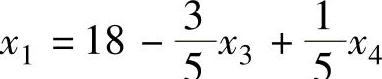，，将其代入目标函数：

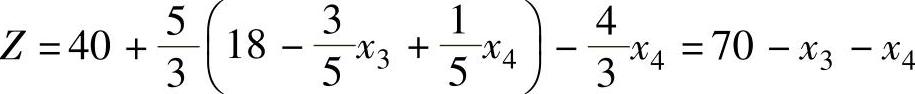
因为λ_j＜0，所以X^（3）=（18，4，0，0）^T是最优解，最优值Z=70。

通过分析上述例题可知，如何通过观察得到一个基本可行解并能判断是否为最优解，关键看模型是不是典则形式（典式）。

所谓典式就是：①约束条件系数矩阵存在m个不相关的单位向量；②目标函数中不含有基变量。满足条件①时立即可以写出基本可行解，满足条件②时马上就可以得到检验数。

以上全过程计算方法就是单纯形法，用列表的方法计算更为简洁，这种表格称为单纯形表，如表1-3所示。

表1-3 单纯形表

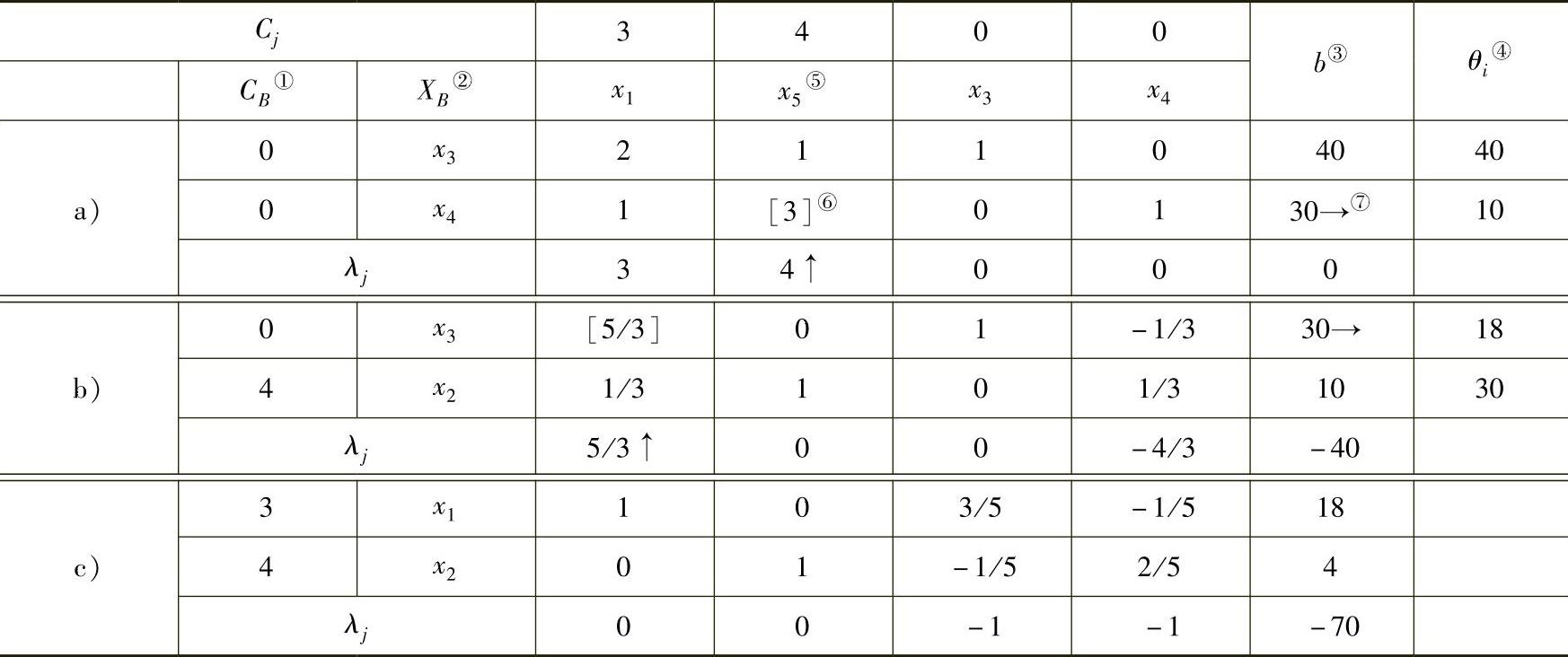
① CB 列为基变量的价值系数。

② XB 列为基变量。

③ b 为约束方程组右端的常数。

④ θ_i为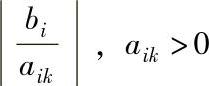，a_ik>0。

⑤ 进基列。

⑥ 主元素。

⑦ 出基行。

综上所述，可将普通单纯形法的计算步骤归纳为：

1）将原问题变换为标准型。(www.daowen.com)

2）找到初始可行基，建立单纯形表，求出检验数。

通常在标准型的系数矩阵A中选择一个m阶单位矩阵或m个线性无关的单位向量作为初始可行基（如表1-3a中x₃、x₄列对应的两个线性无关的单位向量），从而可以求得初始基本可行解。若不存在m阶单位矩阵，则要通过观察或试算寻找可行基，一般采用下面将要介绍的大M法或两阶段单纯形法。

需要说明的是：基变量的检验数必为零。

3）最优性检验。求最大值时得到最优解，求最小值时λ_j≥0得到最优解；某个λ_j≥0（极大化问题），或某个λ_j≤0（极小化问题），且a_ik≤0（i=1，2，…，m），则线性规划具有无界解；存在λ_j≥0（极大化问题），或λ_j≤0（极小化问题）且a_ik（i=1，2，…，m）不完全非正，则进行换基。

4）换基迭代。在选进基变量时，设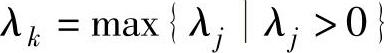（极大化问题），或λ_k=max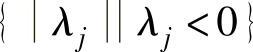（极小化问题），则应选k列的变量x_k为进基变量，如表1-3a中的x₂。在选出基变量时，设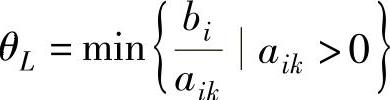，表明第L行的比值最小，则应选L行对应基变量作为出基变量，如表1-3a中的x₄。a_lk为主元素。

需要注意的是：选出基变量时，a_lk必须大于零，小于或等于零没有比值（比值视为无穷大）；若有两个以上相同最小值，任选一个最小比值对应的基变量出基，这时下一基本可行解中存在为零的基变量，称为退化基本可行解。

换基后找到新的可行基（转换为新的典式）。用初等行变换方法将a_lk转换为1，k列其他元素转换为零（包括检验数行），得到新的可行基及基本可行解，再判断其是否是最优解。

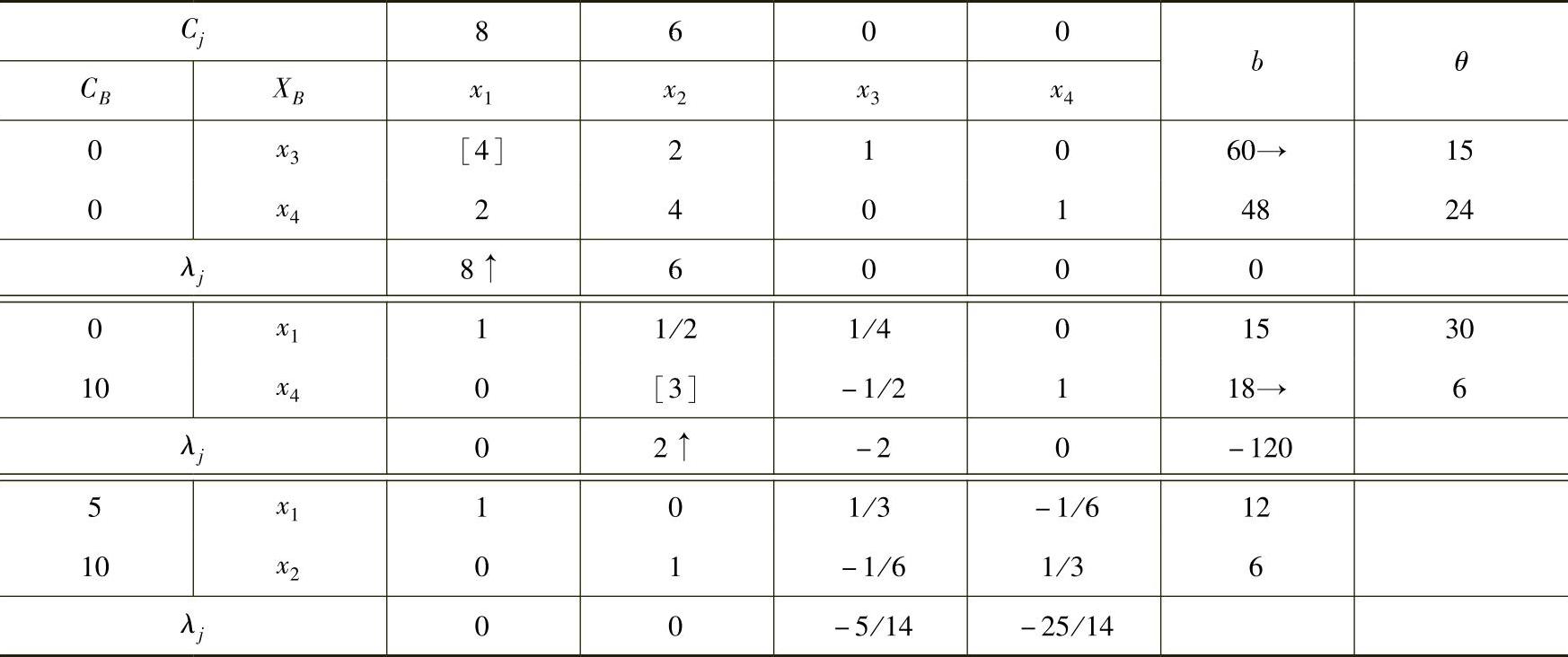
【例1.9】 用单纯形法求解

maxZ=8x₁+6x₂

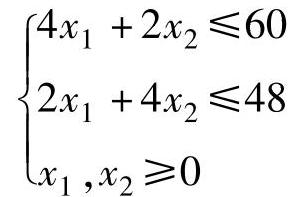
解 将数学模型变换为标准型

maxZ=8x₁+6x₂

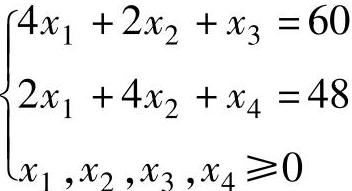
容易看出x₃、x₄可作为初始基变量，单纯形法计算结果如表1-4所示。表的上方增加一行，填写目标函数的系数，目的是用来求非基变量的检验数。检验数可用公式：

λ_j=c_j-C_BP_j计算。见表1-4，初始表中x₁的检验数

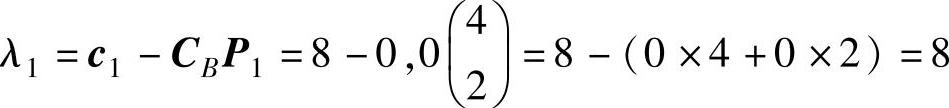
当λ_j≤0时，得到最优解为X=（12，6）^T。

maxZ=8×12+6×6=132

表1-4

【例1.10】 用单纯形法求解

maxZ=-x₁+x₂

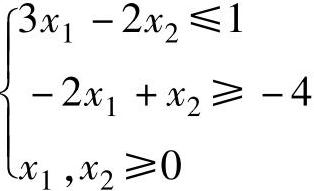
解 将数学模型变换为标准型

maxZ=-x₁+x₂

单纯形法计算该问题的初始单纯形表见表1-5。

表1-5

因为λ₂=1＞0，x₂进基。但是a₁₂＜0，a₂₂＜0，没有比值，说明只要x₂≥0就能保证x₃、x₄非负，即当固定x₁使x₂→+∞时，Z→+∞且满足约束条件，因而原问题具有无界解。

【例1.11】 用单纯形法求解

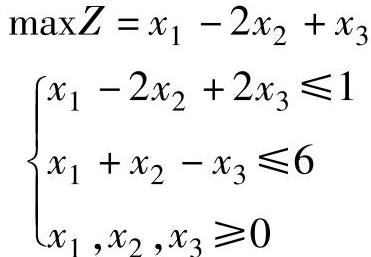
解 将数学模型变换为标准型

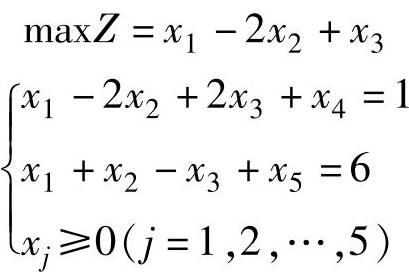
单纯形法计算结果如表1-6所示。

表1-6

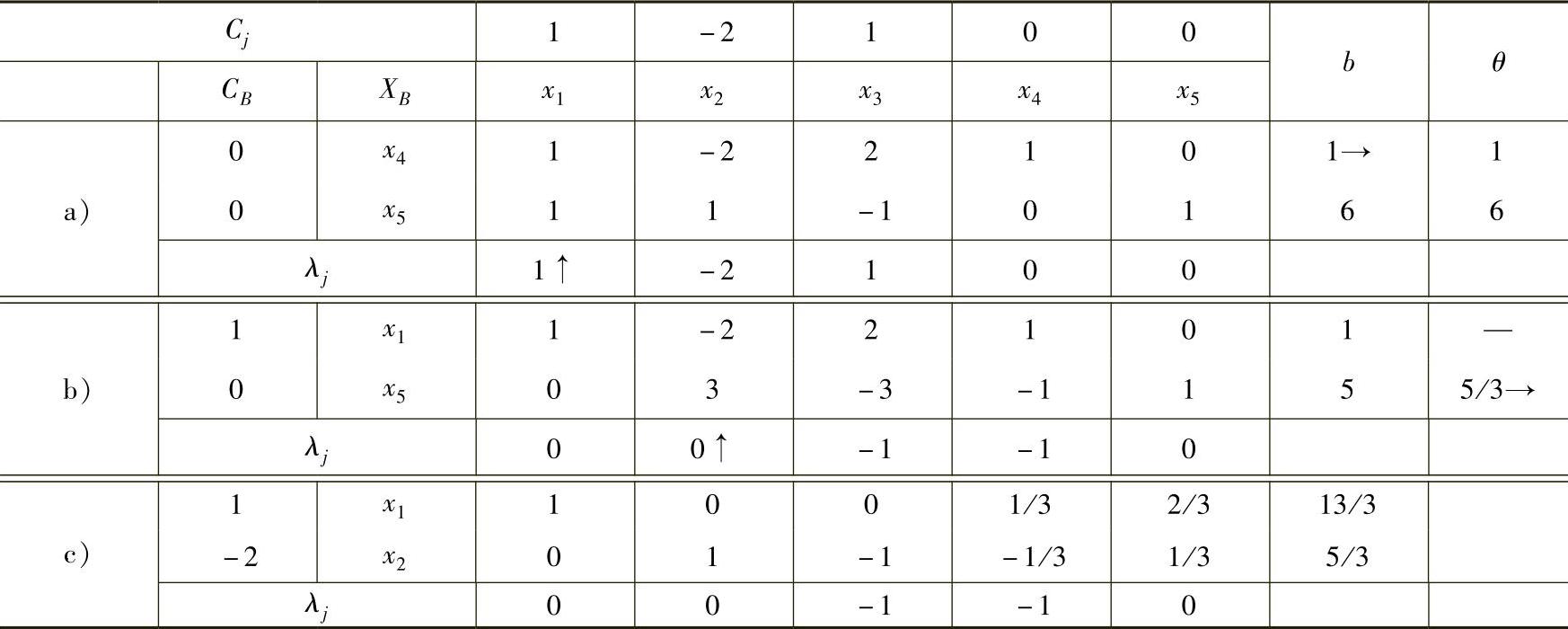
表1-6b中λ_j已经全部非正，得到最优解X^（1）=（1，0，0，0，5）^T，最优值Z=1。

表1-6b中非基变量x₂的检验数λ₂=0，表明若x₂增加，目标函数值不变，即当x₂进基时目标值仍等于1。令x₂进基，x₅出基继续迭代得到表1-6c）的另一个基本最优解。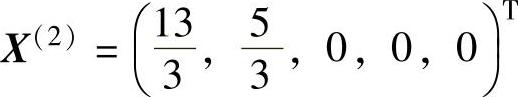

X^（1）、X^（2）是原线性规划的两个最优解，它的凸组合X=αX（1）+（1_-α）X^（2）仍是最优解，即原线性规划问题有多重最优解。

综上所述，单纯形法求解线性规划问题的解的特点如下：

1）最优表中所有非基变量的检验数非零，则线性规划具有唯一最优解。

2）某个λ_k＞0（极大化问题），或某个λ_k<0（极小化问题），且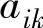≤0（1，2，…，m），则线性规划具有无界解。

3）最优表中存在非基变量的检验数为零，则线性规划具有多重最优解。